Matematica, Anno Accademico 2003-2004, Scienze Geologiche

V.M. Tortorelli

V foglio di esercizi: P.Acquistapace, V.M. Tortorelli

dal 5 novembre 2003 al 12 novembre 2003

Programma e materiale relativo al corso essere reperito in rete selezionando nella Pagina del Dipartimento la voce Materiale Didattico (http://WWW.dm.unipi.it/didactics/home.html) e quindi selezionando ALTRI CORSI DI LAUREA e Corso di laurea *****

-------------------------------------------------------------

Proposizione Se P è un polinomio con coefficienti complessi P(z₀)=0 se e solo se P(z)=Q(z)(z-z₀). Quindi il polinomio ha al più un numero di radici pari al suo grado.

Teorema fondamentale dell'algebra Ogni polinomio ha almeno una radice complessa.

Corollario Un polinomio ha un numero di radici, con molteplicità, pari al suo grado.

Osservazione Un polinomio con coefficienti reali ha radici complesse e coniugate.

------------------------------------------------------------- ESERCIZIO n. 1 Si scrivano in forma cartesiana (x+iy con x e y in R) i seguenti numeri complessi: $(\sqrt{2}+ie)(i-23),~ (-4+4i)^6,~ \frac 1i,~\frac{1+i}{\left(\overline{(2+i)^2}\right)},~ 1+i+i^2+i^4+i^6,~\frac 1{x+iy},~ \sqrt{2+2i}$.

------------------------------------------------------------- ESERCIZIO n. 2 Si trovino tutte le soluzioni in C delle seguenti equazioni: z²+1=0,  z⁶+1=0,  z⁴+1=0,   z²+2z +1=0,  z² +4z +5=0,  z²+2i z -1-i=0, z²+z+1=0.

------------------------------------------------------------- ESERCIZIO n. 3 Si risolvano le seguenti equazioni: $i\bar z^3=\vert z\vert,~~ z^2 +\vert z \vert +1=0,~~ 2z^4 +3z^2=0, ~z\vert z\vert -2{\cal R}\!e z= 0, {\cal I}\!m z^2=1$

------------------------------------------------------------- ESERCIZIO n. 4 Si determino le regioni del piano definite dalle seguenti formule: $\vert z -i\vert=2,~ \vert z-1\vert =\vert z-i\vert ,~\vert z-1\vert <\vert z-i\... ...t =2,~\vert z-1\vert +\vert z-i\vert =\sqrt 2, ~ {\cal R}\! e z=2{\cal I}\! m z$.

------------------------------------------------------------- ESERCIZIO n. 5 - Si scrivano in forma trigonometrica i seguenti numeri complessi: $4, ~7i,~3+3i,~ \sqrt{3} -i,~ 1-i$.

- Si scrivano in forma trigonometrica i numeri complessi z per cui si ripsettivamente : $z= {\cal R}\! e z>0, ~ \vert{\cal R}\! ez\vert < {\cal I}\! m z , ~\vert z\vert \le 1$.

------------------------------------------------------------- ESERCIZIO n. 6 Trovare le radici seste di -1, quadrate di $1+i\sqrt{3}$ e cubiche di 1.

------------------------------------------------------------- Notazione Se $z=x+iy\in {\bf C}$ si indica con e^z il numero $e^x(\cos y +i\sin y)$.

------------------------------------------------------------- ESERCIZIO n. 7 Per ogni numero complesso $w\not= 0$ vi è un numero complesso z per cui w=e^z. Quante sono le soluzioni di w=e^z?

------------------------------------------------------------- ESERCIZIO n. 8 Il prodotto di due numeri compolessi ha come modulo il prodotto dei moduli e come argomento la somma degli argomenti. In altri termini, per quanto enunciato nel precedente esercizio e^z e^w = e^z+w.

------------------------------------------------------------- ESERCIZIO n. 9 - Si verifichi che le radici n-sime di 1 sono $e_h = e^{i 2\pi \frac hn}= \left(e_1\right)^h,~ 0\le h<n$. - Fissati n ed m l'insieme dei $e^{i 2\pi m \frac hn}, ~ h\in {\bf Z}$ è contenuto in quello delle radici n-sime di 1. Coincide con esso se e solo se m ed n non hanno divisori comuni. In altri termini 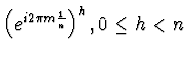$\left(e^{i 2\pi m \frac 1n}\right)^h, 0\le h<n$ sono le radici n-sime di 1 se e solo se m ed n sono primi fra loro.

------------------------------------------------------------- ESERCIZIO n. 10 L'area del triangolo di veritci $u,~v,~w\in{\bf C}$ è data da $\frac 12 \left\vert (w-v)\overline{(u-v)}\right\vert$.

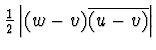------------------------------------------------------------- ESERCIZIO n. 11 - Il prodotto scalare tra (x,y) e (u,v) è dato da ${\cal R}\!e \left( (x+iy)\overline{(u+iv)}\right)$.

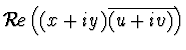- Che operazione tra numeri complessi da il determinante della matrice di righe (x,y), (u,v)?

------------------------------------------------------------- ESERCIZIO n. 12 - Dato $\alpha\in {\bf C}$, trovare la matrice $2\times 2$ (con coefficienti reali) corrispondente alla trasformazione di ${\bf R}^2$ che associa alle coordinate di $z\in {\bf C}$ quelle di $\alpha z$.

- * Le trasformazioni del piano in se che conservano le distanze sono determinate dalle funzioni da ${\bf C}$ in se del tipo $z\mapsto \alpha z +\beta, ~\alpha \bar z + \beta$ per qualche $\beta\in {\bf C}$ e $\alpha\in {\bf C}, ~\vert \alpha \vert =1$.

- Si esprimano mediante operazioni tra numeri complessi le trasformazioni lineari del piano che conservano l'ampiezza degli angoli tra due rette.

------------------------------------------------------------- ESERCIZIO n. 13 - Dati due numeri complessi $\alpha$, $\beta$ e un numero reale $\lambda \geq 0$ si descriva, al variare di tali parametri, la regione del piano determinata dagli $z\in {\bf C}$ per cui $\vert z -\alpha\vert= \lambda\vert z-\beta \vert$.

- Dati i numeri complessi $\alpha,~ \beta,~ \gamma,~ \delta$ per cui $(\alpha ,\beta)\not= \zeta (\gamma , \delta)$ (ovvero $\alpha\delta-\beta\gamma\not= 0$) si mostri che l'inversa della trasformazione $z\mapsto \frac {\alpha z +\beta }{\gamma z +\delta}=w$ è dello stesso tipo.

- Si provi che tali trasformazioni mandano una retta o un cerchio indifferentemente in una retta o in un cerchio.

------------------------------------------------------------- ESERCIZIO n. 14 Si consideri la sfera nello spazio di raggio 1 e centro l'origine. La trasformazione S della sfera meno il ``polo nord'' (0,0,1) che associa ad (x,y,z) sulla sfera l'intersezione della retta per i due punti con il piano z=0 si dice proiezione stereografica.

-a Si scrivano le coordinate (f(x,y), g(x,y), 0) di S(x,y,z). Dato un punto (x,y,0) si scrivano le coordinate ( a(x,y), b(x,y), c(x,y)) del punto sulla sfera che ha il punto dato come proiezione stereografica.

-b ** La proiezione stereografica mantiene gli angoli (l'angolo tra due curve in un loro punto di intersezione è l'angolo tra le eventuali rispettive rette tangenti ad esse nel punto).

------------------------------------------------------------- ESERCIZIO n. 15 Si seplifichino le seguenti espressioni $\log_3 9,~ 25^{\log_5 3},~\log_2 5 -\log_{\frac 12 }10$.

------------------------------------------------------------- ESERCIZIO n. 16 Si tracci un grafico approssimativo di $\log_{\frac 12} (1 +\sin x)$ e di $2^{\tan z}$.

------------------------------------------------------------- ESERCIZIO n. 17 - Dato $w= \rho (\cos\theta +i\sin\theta)\in {\bf C}$ non nullo le soluzioni $z\in {\bf C}$ di w=e^z sono $\log \rho + i (\theta +2k\pi)$ al variare di $k\in {\bf Z}$.

- Si mostri che $z\mapsto e^z$ è invertibile nella regione $-\pi < {\cal I}\!m z \le \pi$. Si provi che la sua immagine su tale regione sono i numeri complessi non nulli e se ne scriva l'inversa.

------------------------------------------------------------- ESERCIZIO n. 18 * Da $\vert x\cos x\vert\le \vert\sin x\vert \le \vert x \vert$ si provi $\frac {\sin x}x \to 1$ e $\frac{{\rm artan} x}x \to 1$ per $x\to 0$

------------------------------------------------------------- ESERCIZIO n. 19 - Si scrivano il modulo e l'argomento di 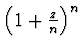$\left(1+\frac z n\right)^n$, $z\in {\bf C}$ e $n\in {\bf N}$ grande.

- * Si calcoli il limite di 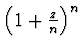$\left(1+\frac z n\right)^n$ per $n\to +\infty$.