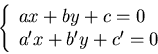
Programma e materiale relativo al corso essere reperito in rete selezionando nella Pagina del Dipartimento la voce Materiale Didattico (http://WWW.dm.unipi.it/didactics/home.html) e quindi selezionando ALTRI CORSI DI LAUREA e Corso di laurea *****
-------------------------------------------------------------
ESERCIZIO n. 1 Dimostrare che il sistema
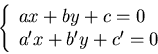
-------------------------------------------------------------
ESERCIZIO n. 2 Determinare la retta passante per ![]() e perpendicolare alla retta
di equazione
e perpendicolare alla retta
di equazione ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 3 Determinare la retta passante per ![]() e per il centro
della circonferenza di equazione
e per il centro
della circonferenza di equazione
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 4 Si calcoli la distanza del punto ![]() dalla retta di equazione
dalla retta di equazione
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 5 Si suddivida il segmento di estremi ![]() e
e ![]() in quattro parti
di egual lunghezza mediante i tre punti
in quattro parti
di egual lunghezza mediante i tre punti ![]() . Si calcolino le coordinate
di tali punti.
. Si calcolino le coordinate
di tali punti.
-------------------------------------------------------------
ESERCIZIO n. 6 Dati ![]() e
e ![]() , trovare le coordinate di un punto
, trovare le coordinate di un punto ![]() sul segmento
sul segmento ![]() tale che
tale che
![]() .
.
------------------------------------------------------------- ESERCIZIO n. 7 Sia ![]() il punto medio del segmento
il punto medio del segmento ![]() , ove
, ove ![]() .
Determinare le coordinate di
.
Determinare le coordinate di ![]() .
.
------------------------------------------------------------- ESERCIZIO n. 8 Dimostrare che per ogni
![]() si ha
si ha
-------------------------------------------------------------
ESERCIZIO n. 9 Provare che il triangolo di vertici ![]() ,
, ![]() e
e ![]() è
isoscele.
è
isoscele.
-------------------------------------------------------------
ESERCIZIO n. 10 Provare che il triangolo di vertici ![]() ,
, ![]() e
e ![]() è
rettangolo.
è
rettangolo.
-------------------------------------------------------------
ESERCIZIO n. 11 Calcolare la lunghezza della mediana uscente dal punto ![]() relativa al
triangolo
relativa al
triangolo ![]() , ove
, ove ![]() ,
, ![]() ,
, ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 12 Scrivere l'equazione dell'asse del segmento di estremi ![]() e
e
![]() (l'asse di un segmento è il luogo dei punti che sono
equidistanti dai vertici del segmento).
(l'asse di un segmento è il luogo dei punti che sono
equidistanti dai vertici del segmento).
-------------------------------------------------------------
ESERCIZIO n. 13 Si provi che le rette di equazioni parametriche ![]() ,
, ![]() e
e
![]() ,
, ![]() sono fra loro parallele se e solo se esiste
sono fra loro parallele se e solo se esiste
![]() , non nullo, tale che
, non nullo, tale che ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 14 Si provi che le rette di equazioni ![]() e
e ![]() sono
fra loro parallele se e solo se esiste
sono
fra loro parallele se e solo se esiste
![]() tale che
tale che
![]() e
e ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 15 Si provi che le rette di equazioni ![]() e
e ![]() sono
fra loro perpendicolari se e solo se esiste
sono
fra loro perpendicolari se e solo se esiste
![]() tale che
tale che
![]() ,
, ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 16 Si provi che le rette di equazioni ![]() ,
, ![]() , e
, e ![]() sono fra loro perpendicolari se e solo se i vettori
sono fra loro perpendicolari se e solo se i vettori ![]() e
e ![]() sono
proporzionali, e sono parallele se e solo se i vettori
sono
proporzionali, e sono parallele se e solo se i vettori ![]() e
e ![]() sono
proporzionali.
sono
proporzionali.
-------------------------------------------------------------
ESERCIZIO n. 17 Si considerino i luoghi dei punti di ![]() descritti dalle
seguenti equazioni:
descritti dalle
seguenti equazioni:
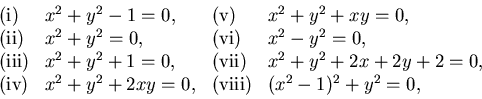

-------------------------------------------------------------
ESERCIZIO n. 18 Si verifichi che ogni angolo convesso è l'intersezione di due
semipiani.
-------------------------------------------------------------
ESERCIZIO n. 19 Si provi che ogni triangolo in ![]() è l'intersezione di tre
semipiani.
è l'intersezione di tre
semipiani.
-------------------------------------------------------------
ESERCIZIO n. 20 Si provi che ogni quadrilatero convesso in ![]() è l'intersezione di
quattro semipiani.
è l'intersezione di
quattro semipiani.
-------------------------------------------------------------
ESERCIZIO n. 21 Verificare che gli insiemi
-------------------------------------------------------------
ESERCIZIO n. 22 Siano
![]() tali che
tali che ![]() . La funzione
. La funzione
![]() ,
definita da
,
definita da
-------------------------------------------------------------
ESERCIZIO n. 23 Siano
![]() tali che
tali che ![]() . La funzione
. La funzione
![]() ,
definita da
,
definita da
-------------------------------------------------------------
ESERCIZIO n. 24 Si provi che se ![]() sono vettori linearmente indipendenti in
sono vettori linearmente indipendenti in ![]() ,
allora per ogni
,
allora per ogni
![]() esiste un'unica coppia di numeri reali
esiste un'unica coppia di numeri reali
![]() tali che
tali che
![]() .
.