Corso di Laurea in Scienze Geologiche, A.A. 2003-2004, Matematica 30 ottobre 2003

Definizione: - Si dice rango di una matrice il numero massimo per cui una sottomatrice quadrata con tale dimensione ha determinante non nullo.

Definizione: Se $A=(a^i_j)_{1\le i\le m, ~1\le j\le n}$ è una matrice con $m$ righe ed $n$ la matrice trasposta è $(a^j_i)_{1\le j\le n, ~1\le i\le m}=_{\rm def}A^t$. Quindi la trasposta di una matrice con una riga ed $n$ colonne $(a, b \dots )$ sarà ${\left({{ a\atop b}\atop \vdots}\right)}$, con $n$ colonne ed una riga.

NOTAZIONE: un elemento di ${\bf R}^d$ considerato come vettore (di spostamento ovvero velocità etc. ) su cui si agisce conviene scriverlo come matrice con $d$ righe ed una colonna. Se si considera come matrice relativa ad un'applicazione lineare da ${\bf R}^d$ ad ${\bf R}$ (come vettore che agisce come forza

Corso di Laurea in Scienze Geologiche, A.A. 2003-2004, Matematica 30 ottobre 2003

Definizione: - Si dice rango di una matrice il numero massimo per cui una sottomatrice quadrata con tale dimensione ha determinante non nullo.

Definizione: Se $A=(a^i_j)_{1\le i\le m, ~1\le j\le n}$ è una matrice con $m$ righe ed $n$ la matrice trasposta è $(a^j_i)_{1\le j\le n, ~1\le i\le m}=_{\rm def}A^t$. Quindi la trasposta di una matrice con una riga ed $n$ colonne $(a, b \dots )$ sarà ${\left({{ a\atop b}\atop \vdots}\right)}$, con $n$ colonne ed una riga.

NOTAZIONE: un elemento di ${\bf R}^d$ considerato come vettore (di spostamento ovvero velocità etc. ) su cui si agisce conviene scriverlo come matrice con $d$ righe ed una colonna. Se si considera come matrice relativa ad un'applicazione lineare da ${\bf R}^d$ ad ${\bf R}$ (come vettore che agisce come ovvero impulso etc. ) come matrice con una riga e $d$ colonne. Nel primo caso le coordinate generiche vengono scritte con indici in alto, nel secondo con indici in basso.

- Questa convenzione si estende quando: si rappresenta una funzione lineare da ${\bf R}^n$ a ${\bf R}^m$ come azione di una matrice con il prodotto (scalare) riga i$^a$ della matrice per colonna del vettore dato per avere la i$^a$ componente del vettore risultato; quando si rappresenta la composizione di due funzioni lineari come prodotto righe per colonne delle matrici ad esse rispettivamente associate.

Esercizio: la relazione tra trasposto e prodottto righe per colonne è $\left( AB\right)^t =B^t A^t$.

- Si dimostra che il rango di una matrice con $m$ righe ed $n$ colonne $A=(a^i_j)_{1\le i\le m, ~1\le j\le n}$ è la dimensione dell'immagine dell'applicazione lineare da ${\bf R}^n$ in ${\bf R}^m$ associata:

$(x^1 , \dots , x^n)^t = {\left( x^1\atop{\vdots\atop {x^n}}\right)} \mapsto \l... ...^{\bf t}= \left( \sum_{1\le j\le n } a_{j}^i x^j \right)_{1\le i\le m}^{\bf t}$

Definizione: - Il luogo di zeri di una funzione polinomiale di secondo grado in $n$ variabili:

$$\sum_{1\le i, j\le n } a_{j}^i x^j x_i ~+~ 2\sum_{1\le i \le ... ...{\bf x} ~+~ 2{\bf b}^t{\bf x} +c ~,~~ A\not= {\bf0}_{n\times n}$$

$$\widetilde{\bf x}^t\widetilde A \widetilde{^{\,}{\bf x}}~,~~\... ...verline{~\phantom{b} A}}\right)}~,~~ A\not= {\bf0}_{n\times n}$$

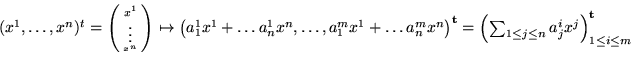
si dice quadrica. Se $n=2$ conica. Una quadrica si dice non degenere se ${\rm det} \widetilde A\not=0$.

Osservazione: Poiché: $\sum a_{ij}x_i x_j ~=~\sum \frac{a_{ij} +a_{ji}}2 x_i x_j$, si assume che $A$, e quindi $\widetilde A$, sia una matrice simmetrica; i.e. $a_{ij } =a_{ji}$.

Osservazione: si é identificato ${\bf x}\in{\bf R}^n$ con il sottospazio affine degli $\left({x^0\atop{\!\! {\bf x}}}\right)\in {\bf R}^{n+1}$ con la prima coordinata eguale ad $1$: $x^0=1$. Conviene quindi osservare che il gruppo affine su ${\bf R}^n$ puó essere identificato con un sottogruppo, del gruppo lineare su ${\bf R}^{n+1}$, che agisce su tale sottospazio affine di ${\bf R}^{n+1}$ nel seguente modo: alla trasformazione affine ${\bf x}\mapsto {\bf w}+N{\bf x}$ da ${\bf R}^n$ in se si associa l'azione della matrice:

$$\left( \left.{ 1\atop { \overline{{\bf w}\phantom{N}}\!\!\! }... ...top {\bf x}}\right) ~=~\left({1\atop {\bf w}+ N{\bf x}}\right)$$

$$\left( \left.{ 1\atop { \overline{{\bf z}\phantom{P}}\!\!\! }... ...t {{\bf0}^t\atop\!\!\!\overline{~ N^{-1}}}\right)} = Id_{n+1}$$

Nelle variabili ${\bf y}= -{\bf v} +M^{-1}{\bf x}$, considerando che $\widetilde {\bf x} = {\left(\left.{ 1\atop{ \overline{M{\bf v}~}\!\!\! } }\right\vert {{\bf0}^t\atop\!\!\!\overline{~ M}}\right)} \widetilde {\bf y}$, si ottiene :

$$\widetilde{\bf y}^t \left[ { \left(\left.{ {1~}\atop{ \overl... ...t\atop\!\!\!\overline{~ M}}\right)} \right] \widetilde {\bf y}$$

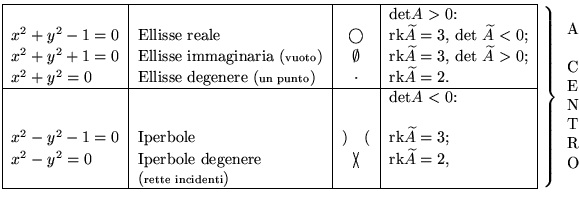
CLASSIFICAZIONE AFFINE DELLE CONICHE

Ogni conica puó essere trasformata in una delle seguenti con un cambiamento di coordinate affine del tipo ${\bf x}\mapsto {\bf w}+N{\bf x}$.

$\!\!\!\left. \hbox{ \begin{tabular}{\vert l \vert l \vert c \vert l \vert} \hli... ...{\rm C}\\ {\rm E}\\ {\rm N}\\ {\rm T}\\ {\rm R}\\ {\rm O}\\ \end{array}~~$

$\phantom{x^2 +y^2 -1 =0\!}$			${\rm det}A =0$:
$y^2 -x =0$	Parabola	$\bigcup\!\!\!\!\cdot ~$	rk $\widetilde A=3$, rk$A=1$
$y^2 -1=0$	Parabola degenere	$=\!\! =\!\!=$	rk $\widetilde A=2$, rk$A=1$
	( )		$\phantom{{\rm rk}\widetilde A=3{\rm , ~det}\widetilde A<0{\rm ;}~\!}$
$y^2 +1=0$	Parabola degenere (	$\emptyset$	rk $\widetilde A=2$, rk$A=1$
	)
$y^2 =0$	C. doppiamente degenere	$-\!\!\!\! -\!\!\!\! -$	rk $\widetilde A=1$
	( )

Una famiglia di invarianti classificante é quindi data da ${\rm sign}({\rm det} A)$, ${\rm rk}\widetilde A$, ${\rm rk}A$, ${\rm sign}({\rm det} \widetilde A)$.
CLASSIFICAZIONE AFFINE DELLE QUADRICHE NON DEGENERI

Ogni quadrica non degenere puó essere trasformata in una delle seguenti con un cambiamento di coordinate affine.

		rk $\widetilde A=n+1$
$\sum_{i=1}^p (x^i)^2 -\sum_{i=p+1}^n(x^i)^2 -1 =0$	Tipo ellisse-iperbole	${\rm det}A \not= 0$
$\sum_{i=1}^p (x^i)^2 ~-\sum_{i=p+1}^{n-1}(x^i)^2 ~-x^n =0$	Tipo parabola	${\rm rk}A = n-1$

QUADRICHE NELLO SPAZIO

		${\rm det}A > 0$
$x^2 +y^2 +z^2 -1 =0$	Ellissoide	${\rm rk}\widetilde A=4$, ${\rm det}\widetilde A<0$
$x^2 +y^2 +z^2 +1 =0$	Ellissoide immaginario	${\rm rk}\widetilde A=4$, ${\rm det}\widetilde A>0$
	( )
$x^2 +y^2 +z^2 =0$	Ellissoide degenere	${\rm rk}\widetilde A=3$, ${\rm det}\widetilde A=0$
	( )
		${\rm det}A <0$
$x^2 +y^2 -z^2 -1=0$	Iperboloide iperbolico	${\rm rk}\widetilde A=4$, ${\rm det}\widetilde A>0$
	ad una falda
$x^2 +y^2 -z^2 +1=0$	Iperboloide ellittico	${\rm rk}\widetilde A=4$, ${\rm det}\widetilde A<0$
	a due falde
$x^2 +y^2 -z^2 =0$	Iperboloide degenere	${\rm rk}\widetilde A=3$, ${\rm det}\widetilde A=0$
	( )
		${\rm det}A =0$, ${\rm rk}\widetilde A=4$
$x^2+y^2 -z =0$	Paraboloide ellittico	${\rm rk}A =2$
		${\rm det}\widetilde A<0$
$x^2 -y^2 -z=0$	Paraboloide iperbolico	${\rm rk}A =2$
	( )	${\rm det}\widetilde A>0$
		${\rm det}A =0$, ${\rm rk}\widetilde A=3$
$x^2-y =0$	Paraboloide degenere	${\rm rk}A =1$
	(
$x^2\pm y^2 \pm 1 =0$	Cilindri su coniche non	${\rm rk}A =2$
	degeneri con centro,
	eventualmente il vuoto
		${\rm det}A =0$, ${\rm rk}\widetilde A=2$
$x^2\pm 1=0$	Vuoto o piani paralleli	${\rm rk}A =1$
$x^2\pm y^2 =0$	Retta o piani incidenti	${\rm rk}A =2$
		${\rm det}A =0$, ${\rm rk}\widetilde A=1$
$x^2=0$	Piano``doppio''	${\rm rk}A =1$