Next: About this document ...
Esame di Matematica - Scienze geologiche
Prova scritta del 14 gennaio 2004 -
tema n.1
Prima parte
Esercizio 1 Date le rette 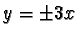 e fissato il punto
P=(-5,-12), trovare due numeri positivi a e b tali che l'iperbole
di equazione
e fissato il punto
P=(-5,-12), trovare due numeri positivi a e b tali che l'iperbole
di equazione
passi per P ed abbia tali rette come asintoti.
Esercizio 2 Si consideri la successione definita da
e se ne calcoli il limite (se esiste) al variare del parametro
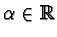 .
.
Seconda parte
Esercizio 3 Data la funzione
se ne determinino:
- (i)
- i punti di massimo e di minimo relativo,
- (ii)
- i limiti a
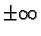 ,
,
- (iii)
- gli eventuali asintoti.
Esercizio 4 Calcolare l'integrale
Esame di Matematica - Scienze geologiche
Prova scritta del 14 gennaio 2004 -
tema n.2
Prima parte
Esercizio 1 Date le rette 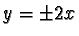 e fissato il punto
P=(-13,-24), trovare due numeri positivi a e b tali che l'iperbole
di equazione
e fissato il punto
P=(-13,-24), trovare due numeri positivi a e b tali che l'iperbole
di equazione
passi per P ed abbia tali rette come asintoti.
Esercizio 2 Si consideri la successione definita da
e se ne calcoli il limite (se esiste) al variare del parametro
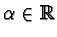 .
.
Seconda parte
Esercizio 3 Data la funzione
se ne determinino:
- (i)
- i punti di massimo e di minimo relativo,
- (ii)
- i limiti a
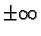 ,
,
- (iii)
- gli eventuali asintoti.
Esercizio 4 Calcolare l'integrale
Istruzioni per l'uso
Questa prova scritta può essere utilizzata nei modi seguenti.
- Risolveranno soltanto gli esercizi della prima parte gli studenti del
primo anno che:
- hanno fatto male il primo compitino e bene il secondo;
- hanno fatto bene i due compitini ma il primo peggio del secondo.
In questi casi la votazione (in trentesimi) della prima parte farà media
col voto del secondo compitino, e, se non inferiore a 18, ammetterà
all'orale. Si considererà comunque la migliore fra la vecchia media dei
compitini e la nuova media ottenuta con questa prova.
- Risolveranno soltanto gli esercizi della seconda parte gli
studenti del primo anno che:
- fatto male il secondo compitino e bene il primo;
- hanno fatto bene i due compitini ma il secondo peggio del primo.
In questi casi la votazione (in trentesimi) della seconda parte farà media
col voto del primo compitino, e, se non inferiore a 18, ammetterà
all'orale. Si considererà comunque la migliore fra la vecchia media dei
compitini e la nuova media ottenuta con questa prova.
- Risolveranno gli esercizi sia della prima che della seconda parte gli
studenti del primo anno che:
- hanno fatto male entrambi i compitini;
- hanno fatto bene i compitini ma vogliono migliorare la propria media.
In questi casi la media dei voti (in trentesimi) relativi alle due parti,
se non inferiore a 18, ammetterà all'orale. Si considererà comunque la
migliore fra la vecchia media dei compitini e la nuova media ottenuta con
questa prova.
- Gli studenti dgli anni successivi al primo hanno diritto a sostenere
la sola prova orale. Se fanno questa prova scritta, per intero o (avendo
fatto i compitini) solo in parte, potranno sostenere una prova orale più
snella e solo teorica (senza esercizi), come quella degli studenti del primo
anno.
Le prove orali degli studenti che sostengono questa prova devono essere
sostenute entro la sessione di esami di gennaio-febbraio 2004. Chi non
sostiene l'orale entro questo termine, dovrà ricominciare da capo con una
nuova prova scritta nelle sessioni successive.
Soluzioni
Esercizio 1 Indichiamo con (-u,-v) le coordinate di P (per
il tema n.1 si ha u=5, v=12 e per il tema n.2 si ha u=13, v=24);
similmente, indichiamo con 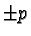 i coefficienti angolari delle due
rette (per il tema n.1 si ha p=3 e per il tema n.2 si ha p=2). La
prima condizione da imporre è che l'iperbole passi per P: quindi
deve essere
i coefficienti angolari delle due
rette (per il tema n.1 si ha p=3 e per il tema n.2 si ha p=2). La
prima condizione da imporre è che l'iperbole passi per P: quindi
deve essere
Gli asintoti si trovano osservando che l'equazione dell'iperbole si
scinde nelle due seguenti:
Analizziamo la prima equazione, cioè quella col segno +, relativa
al ramo superiore dell'iperbole. Per
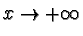 si ha, essendo
si ha, essendo
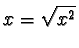 ,
,
Analogamente, per
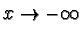 si ha, essendo
si ha, essendo
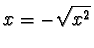 ,
,
Dunque il ramo superiore dell'iperbole (y>0) ha per asintoti obliqui
la retta
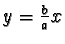 per
per
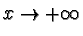 e la retta
e la retta
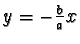 per
per
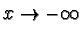 .
.
Il ramo inferiore (y<0), per motivi di simmetria rispetto all'asse x,
avrà per asintoti obliqui la retta
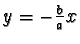 per
per
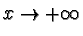 e la retta
e la retta
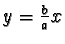 per
per
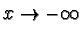 .
.
In definitiva, dobbiamo richiedere ai coefficienti a e b la
condizione
Dobbiamo dunque risolvere il sistema
ricordando che si richiede a>0, b>0.
Per il tema n.1 la soluzione è a=3 e b=9; per il tema n. 2 la
soluzione è a=5 e b=10.
Esercizio 2 Per il tema n.1 si ha
Se 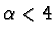 il limite è
il limite è 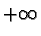 in quanto la frazione si
comporta come
n2+4-4/2, ossia come n4. Se
in quanto la frazione si
comporta come
n2+4-4/2, ossia come n4. Se 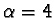 il
denominatore va come 2n2 e il numeratore è -4n2, per cui
il limite è -2. Infine se
il
denominatore va come 2n2 e il numeratore è -4n2, per cui
il limite è -2. Infine se 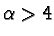 l'intera frazione si comporta
come
l'intera frazione si comporta
come
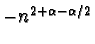 e quindi il limite è
e quindi il limite è 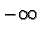 .
.
Per il tema n.2 invece si ha
Se 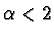 il limite è
il limite è 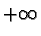 in quanto la frazione si
comporta come
n1+2-2/2, ossia come n2. Se
in quanto la frazione si
comporta come
n1+2-2/2, ossia come n2. Se 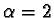 il
denominatore va come 2n e il numeratore è -2n, per cui
il limite è -1. Infine se
il
denominatore va come 2n e il numeratore è -2n, per cui
il limite è -1. Infine se 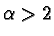 l'intera frazione si comporta
come
l'intera frazione si comporta
come
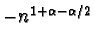 e quindi il limite è
e quindi il limite è
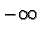 .
.
Esercizio 3 La funzione del tema n.2 si ottiene da quella del
tema n.1 cambiando x con -x: quindi il suo comportamento è il
simmetrico rispetto all'asse y di quello della funzione del tema
n.1. Analizziamo quindi la funzione del tema n.1 e cioè
(i) Si ha
La funzione è sempre non negativa ed è nulla per 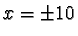 :
tali
punti sono quindi punti di minimo assoluto, quindi anche relativo.
:
tali
punti sono quindi punti di minimo assoluto, quindi anche relativo.
Cerchiamo i punti di massimo relativo. In [-10,10] si ha
quindi in tale intervallo si ha
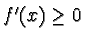 se e solo se
se e solo se
cioè se e solo se
Poiché
la funzione ha un massimo relativo in
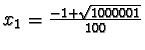 .
.
In
![$[10,\infty[ \cup ]-\infty,-10]$](img51.gif) si ha
si ha
quindi
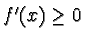 se e solo se
se e solo se
essendo, come sappiamo,
il punto
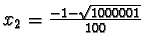 è di massimo
relativo.
è di massimo
relativo.
Per la funzione del tema n.2 si avrà che i punti di minimo relativo
sono ancora 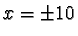 ,
mentre i punti di massimo relativo sono
,
mentre i punti di massimo relativo sono
(ii) Si ha, per la funzione del tema n.1,
Per la funzione del tema n.2 si ha, analogamente,
(iii) La funzione del tema n.1 ha l'asintoto orizzontale y=0
per
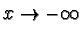 .
Poiché inoltre
.
Poiché inoltre
essa non ha asintoto per
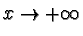 .
Per la funzione n.2,
simmetricamente, c'è l'asintoto orizzontale y=0 per
.
Per la funzione n.2,
simmetricamente, c'è l'asintoto orizzontale y=0 per
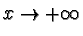 e non c'è asintoto per
e non c'è asintoto per
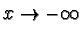 .
.
Esercizio 4 Calcoliamo l'integrale del tema n.1: con la
sostituzione
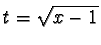 si ha x=1+t2,
si ha x=1+t2,
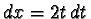 e quindi
e quindi
Calcoliamo l'integrale del tema n.2: con la
sostituzione t=ex si ha 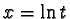 ,
dx = dt/t e quindi
,
dx = dt/t e quindi



Next: About this document ...
Vincenzo Maria Tortorelli
2004-01-16
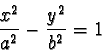
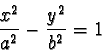
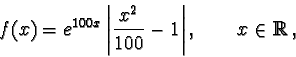
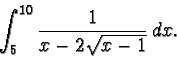
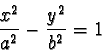
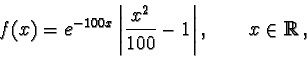
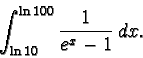
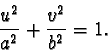
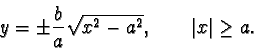
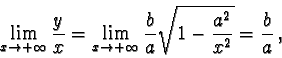
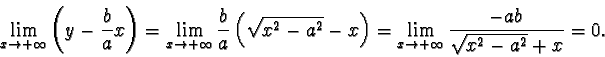
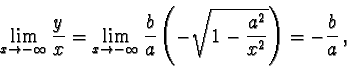
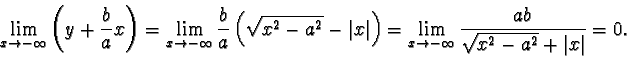
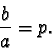
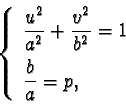
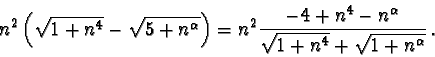
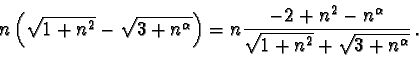
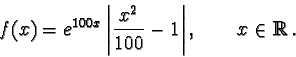
![\begin{displaymath}f(x) = \left\{ \begin{array}{ll}
\displaystyle{e^{100x} \le...
...}{100}\right)} & \textrm{se }
x\in [-10,10].\end{array}\right.\end{displaymath}](img42.gif)
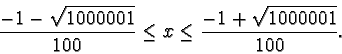
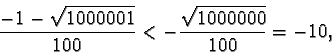
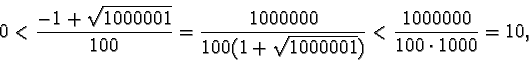
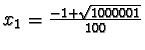 .
.
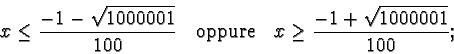
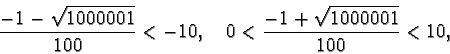
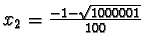 è di massimo
relativo.
è di massimo
relativo. 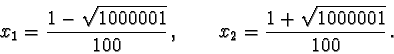
![\begin{eqnarray*}\int_5^{10} \frac{1}{x-2\sqrt{x-1}} \, dx & = & \int_2^3
\frac...
...ac{2}{t-1} \right]_2^3 = 2 \ln 4 - 1+
2=\\
& = & 4\ln 2 +1.
\end{eqnarray*}](img62.gif)