Riferimenti (per la lezione in oggetto):[EB] cap. 1 pagg. 1-10, [VV] cap. 3 pagg. 38-47, [MA1] cap. 1 pagg. 1-10, [EB] cap. 8 pagg. 202-209 (da rileggere in seguito).
1-Richiami e osservazioni sulla raccolta di dati: scale nominali, ordinali e rapportali. Numeri naturali ed interi, minore e ``minore o uguale''.
2- Richiamo della definizione di logaritmo in base positiva.
Frazioni e numeri razionali, notazione decimale allineamenti finiti e periodici.
La grandezza lineare della diagonale del quadrato non e' commensurabile con quella del lato: provando a riportare il lato sulla diagonale e continuando a cercare di ricoprire con il resto il resto precedente si ottiene una ``costruzione geometrica che non termina'' perche' in due passi ci si riconduce ancora a riportare il lato di un quadrato (parallelo al primo e piu' piccolo) sulla sua diagonale:
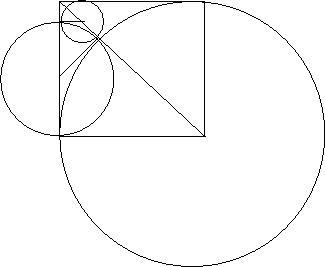 . Considerando il lato del quadrato unitario, la misura numerica
x della lunghezza della diagonale non potra' essere razionale. In
effetti per il teorema di Pitagora dovrebbe essere x^2=2. Si e' appena
visto che questa equazione non puo' avere soluzioni razionali con una
costruzione geometrica che prescinde dai numeri. Si puo' viceversa
. Considerando il lato del quadrato unitario, la misura numerica
x della lunghezza della diagonale non potra' essere razionale. In
effetti per il teorema di Pitagora dovrebbe essere x^2=2. Si e' appena
visto che questa equazione non puo' avere soluzioni razionali con una
costruzione geometrica che prescinde dai numeri. Si puo' viceversa facilmente trovare una prova algebrica di questo fatto: se x fosse la frazione ``irriducibile'' m/n si avrebbe m^2= 2 n^2 , ma allora m sarebbe pari (un dispari per se stesso e' dispari!), m=2k, e quindi 4k^2= 2n^2 cioe' 2k^2=n^2 ma allora anche n sarebbe pari come m, mentre la frazione m/n era irriducibile.
3- Richiamo di prodotti notevoli
A^2-B^2= (A-B)(A+B)
A^3-B^3=(A-B)(A^2 + AB+B^2)
A^4-B^4=(A^2-B^2)(A^2+B^2)=(A-B)(A+B)(A^2+B^2)=(A-B)(A^3+ A^2B +AB^2 +B^3)
Piu' in generale, con la giusta osservazione, si ottiene per ogni esponente naturale n
A^n -B^n = (A-B)( A^(n-1) + A^(n-2) B + ...+ AB^(n-2) +B^(n-1))
per A=1 si ottiene un fattore che e' la somma delle potenze crescenti da 0 a n-1 di B
1-B^n=(1-B)(1+B+...+B^(n-1)).
4- Numeri reali per misurare, allineamenti decimali infiniti cosa vuol dire 0.c1c2c3...ck... con una cifra intera ck tra 0 e 9 per ogni numero naturale k, tra l'altro senza specificare alcuna regola
che ci permetta il calcolo della cifra al generico posto k ?
4.1- Parentesi teorica
La proprieta' fondamentale dei numeri reali:
dati dei numeri M1 M2, ... Mk ... al variare di k tra i naturali
1-se per ogni soglia di errore E>0 vi e e' n naturale per cui se h, k> n allora -E< Mk-Mh<E
allora vi e' un reale L per cui
2- per ogni errore E'>0 vi e' m naturale per cui se k>m allora -E'< Mk -L<E'
(qualitativamente si puo' dire che:
comunque dati infiniti numeri M1 M2, ... Mk ...
1'- che si avvicinano tra loro sempre di piu'
allora vi e' un numero L
2'- a cui si avvicinano sempre piu')
Questa proprieta' permette di affermare che vi sono sempre le radici di numeri positivi,
le potenze ad esponente reale di una base positiva, i logaritmi etc. etc. .
Tale proprieta' , che si assume, si dice completezza per successioni dei numeri reali.
Le successioni che soddisfano la condizione 1 si dicono di Cauchy.
La condizione 2 e' la definizione della convergenza della successione a L per n che tende all'infinito, si dice anche che L e' limite della successione Mn per n che tende all'infinito.
In altre parole la proprieta' e' ogni successione di Cauchy converge a qualche numero.
Chiusa parentesi teorica
4.2 -Esercizio
Per tornare agli allineamenti decimali infiniti
date per ogni numero naturale k le cifre tra 0 e 9 c1, c2, c3 , ... ck considera
Mk = c1/10 + c2/100 ... + ck/10^k = 0.c1c2 c3 ... ck < o = Mk+1= Mk +ck+1 /10^(k+1)
fissa un' arbitraria soglia di errore E>0
ci si domanda se per k>h naturali abbastanza grandi E> Mk- Mh > -E, in effetti si ha
0 < o = Mk - Mh=ch+1/10^(h+1) + ... + ck/10^k < o =
9(1/10^(h+1) + ... + 1/10^k ) e questo e' il passaggio in cui dei ck si usa solo il fatto che sono tutti minori di 10
= 9/10^(h+1) (1+ ...+ 1/10^(k-h-1)) < 9/10^(h+1) 1. 1periodico= 9/10^(h+1)10/9=
= 1/10^h che e' minore di E per tutti gli h maggiori di LOG10 1/E
appunto il numero di iterazioni minimo per cui gli Mk differiscono tra loro per meno di E e' il piu' piccolo naturale n maggiore di LOG10 1/E.
Usando quindi la proprieta' fondamentale dei reali si asserisce che vi e' un numeo reale L
a cui si avvicinano sempre piu' aumentando opportunamente il numero di cifre k i numeri
0.c1c2 c3 ... ck.
Le scritture 0.c1c2 c3 ... ck... (allineamento decimale infinito) ovvero
c1/10 + c2/100 ... + ck/10^k +... (somma infinita di termini non negativi) sono giustificate ed indicano (ed individuano) il numero L. Si scrivera':
L=0.c1c2 c3 ... ck... =c1/10 + c2/100 ... + ck/10^k +...
Fine esercizio.
4.3 - Serie geometriche di ragione x:
utilizzando il prodotto notevole 1-x^n =(1-x)(1+x+x^2+...x^(n-1)) si ha
1+x+x^2+...x^(n-1) = (1-x^(n-1))/(1-x), e se -1< x< 1 per n che aumenta x^(n-1) diventa sempre piu' piccolo e quindi per -1< x< 1 non solo ha senso la somma infinita
1+x+x^2 +... ma si sa che e' anche eguale a 1/(1-x).
Per le serie geometriche non serve la proprieta' fondamentale dei numeri reali si sa a priori che il numero L cui si avvicinano le somme approssimanti e' 1/(1-x) !
Si usa solo il fatto che se -1< x< 1 allora x^n diventa sempre piu' piccolo e la formula per 1-x^n.
Nota tale affare e' vero anche per x=-1 ma l'argomento per arrivarci e' diverso.
5- Sull'uso dei puntini: se si scrive 1, 2, ... 5 si intende di solito 1, 2, 3, 4, 5 cioe' l'uso dei puntini e' una mera abbreviazione tipografica. In molti casi vi e' un uso dei punti ad esso ispirato ma che e' solo una notazione suggestiva, proprio perche' suggerisce l'abbrevazione a cui appena accennato di uso comune, per indicare che si sta dando una definizione ``implicita''.
Considerando per esempio la scrittura
Mk= 1/10 + 2/100 ... + k/10^k al variare di k tra i naturali
si intende semplicemente che M0=0 e Mk+1= Mk + (k+1)/10^(k+1), una definizione ben precisa.
Definizioni date in questa maniera si dicono definizioni per ricorrenza.
Si nota che usando solo la definizione degli Mn, per calcolare Mk ci vogliono almeno k-1 addizioni e k-1 divisioni (generando magicamente i numeri naturali e le potenze di 10).
In una definizione ``esplicita'' invece il numero di operazioni e' fisso: quante se ne scrivono!
Sk = 3+ k/(k+1) richiede una divisione e una somma.
6- Interpretazione geometrica dei numeri reali: la retta il ``continuo geometrico unidimensionale''. Quindi le due astrazioni si fanno usualmente coincidere e si identificano i numeri reali con la retta munita di un sistema di riferimento:
- si fissa un 'origine O (lo 0)
- un verso di crescita (usualmente da sinistra a destra cosicche' un punto della retta a destra di un altro rappresenta un numero maggiore)
- un unita' di misura (il numero 1) .
Le somma tra numeri p+v si puo' identificare con un percorso lungo v a partire da p: a destra se p e' positvo a sinistra se p e' negativo.
Nota : val la pena notare che in questo caso il numero p fa le veci di un punto di partenza mentre il numero v quelle di uno spostamento.
La moltiplicazione mp nel considerare il segmento Op allungato di un fattore m, se m e' positivo, mentre se m e' negativo nel suo simmetrcio rispetto ad O.
La proprieta' fondamentale dei numeri reali si traduce nel fatto intuitivo che la retta non ha ``buchi'', appunto si dice che costituisce un continuo per cui se infiniti punti si accumulano vi deve essere un punto loro limite.
Notazioni:notazione per successioni, logb a (a>0, b>0) minore o eguale, notazione esponenziale e per le radici aritmentiche, uso dei puntini per un numero indeterminato di termini
Definizioni:logaritmo, successione, serie, somme infinite come serie i cui valori si avvicinano a sempre piu' ad un numero
Enunciati: la diagonale del quadrato e' incommensurabile con il lato dello stesso (dim), 2 non e' il quadrato di un numero razionale ovvero la radice qudrata di 2 non e' razionale (dim),
a^n -b^n =(a-b)(a^n-1 + a^n-2b +... + ab^n-2 + b^n-1),
prima proprieta' fondamentale dei numeri reali, gli allineamenti decimali infiniti corrispondono a serie convergenti (dim), le serie geometriche convergono se la ragione e' tra -1 e 1 (dim).
3-10-08 esercitazione 1 (Mauro) materiale sistemi di disequazioni di razionali, equazioni e disequazioni per trinomi in una variabile, [VV] cap. 4 pagg. 55-69.
6-10-08 lezione 2 (Tortorelli) Riassunto della e precisazioni sulla precedente lezione, uso della corrente terminologia matematica.
Riferimenti: [EB] cap. 1 pagg 13-14, 20-21, cap. 6 pagg. 143-146, cap. 8 pagg. 209-217,
[BDM]cap. 1 pagg. 33-40, 48-52, 54-58 (distanze), cap. 7 pagg. 278-292 (da rileggere in seguito), [VV] cap. 3 pagg. 48-51.
La proprieta' di Archimede: 1/n converge a 0 per n che tende all'infinito.
Definizioni per ricorrenza di una successione:
il termine n+1 di una successione puo' essere calcolato con una formula che coinvolge i numeri da 1 a n e i termini gia' calcolati della successione
Mn+1 = F(1, ..., n, M1, ... Mn )
esempi: data la successione ... an ... la definizione per ricorrenza Sn+1= Sn + an+1 e' la successione delle successive somme a1+...+ an+1; fn+1 = fn (n+1) e' la definizione per ricorrenza del prodotto dei primi n numeri naturali, detto il fattoriale di n; Fn+2 = Fn+Fn+1 e' la legge di ricorrenza di Fibonacci se per esempio F0=0 e F1=1 si ha F2=1, F3=2, F4= 3, F5=5, F6=8, F7=13 ... .
Interpretazione geometrica dei numeri reali, valore assoluto e distanze, intervalli semirette.I numeri e e pi-greco.
Notazioni:notazioni per la convergena e per il limite, N, Z, Q, R, [a, b], [a,b[, [a,b) etc. ,
]-oo, b], etc. , il simbolo dell'appartenenza (epsilon stampatello minuscolo), il segno dell'inclusione tra insiemi, |x|, e, notazione per l'area un cerchio unitario ``pi-greco''
Definizioni:. successione di Cauchy, successione convergente e limite di una successione, successione definita per ricorrenza: successione crescente, successione limitata superiormente,
intervalli chiusi aperti , semirette chiuse aerte, valore assoluto, distanza astratta su una popolazione:
dist(a,b) >o= 0, dist (a,b)= 0 se e solo se a=b
dist(a,b) = dist(b,a)
dist(a,b) <o= dist(a,c)+dist(c,b)
punto medio, algoritmo di bisezione per il calcolo approssimato delle radici
per ricorrenza:
dati a0 e b0 per cui 0< a0^k < x< b0^k
se ((an +bn)/2)^k < x si pone an+1 = (an +bn)/2 e bn+1=bn
se ((an +bn)/2)^k > x si pone an+1 = an e bn+1=(an +bn)/2,
la successione del tasso di interesse composto ( 1+ x/n )^n,
il numero di Nepero e e la sua successione approssimante ( 1+ 1/n )^n,
il numero pi-greco.
Enunciati: la prima proprieta' fondamentale dei numeri reali si chiama completezza sequenziale, e dice: ogni successione di Cauchy e' convergente.
La seconda proprieta' fondamentale dice che dato un numero reale vi e' sempre un numero naturale piu' grande. Si chiama proprieta' di Archimede ed e' equivalente a dire che la successione dei reciproci dei numeri naturali converge a 0: 1/n --> 0 per n -->+00.
Se una succcessione e' crescente e limitata superiormente allora converge.
Si ha: |x-y| < o = |x| + |y|.
Il valore assoluto e' una distanza.
Le successioni date dalla bisezione convergono alla radice k del numero x:
- infatti si ha sempre 0< an < bn, bn-an = (b0-a0)/2^n,
quindi dall'indice 2n in poi la successione a0, b0, a1, b1, a2, b2 ... sta nell' intervallo [an, bn] che misura (b0-a0)/2^n, quindi e' di Cauchy, quindi e' convergente ad un limite L.
- d'altra parte an^k< x< bn^k , facendo il limite si ottiene: L^k < o = x < o = L^k cioe'
L^k=x.
La successione del tasso di interesse composto x, ( 1+ x/n )^n, per i naturali maggiori di -x e' crescente, inoltre e' limitata superiormente. Il limite di ( 1+ 1/n )^n si chiama e costante di Nepero.
Si prova che ( 1+ x/n )^n ---> e^x per n---> +oo.
La successione Sn= somma delle aree dei quadrati di lati 1/2^n contenuti nel cerchio di raggio uno, disposti per un vertice a partire dal centro con lati tra loro paralleli ed allineati
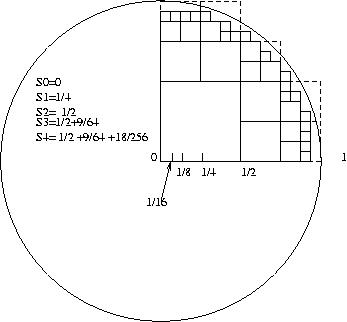 e'crescente (diminuendo il lato
da 1/2^n a 1/2^(n+1) i quadrati gia'
contenuti nel cerchio si dividono in quattro, e si
aggiungono alcuni quarti di quelli che prima attraversavano la
circonferenza), e' limitata superiormente
da 4 (il quadrato di lato 2 contiene il cerchio) quindi converge.
e'crescente (diminuendo il lato
da 1/2^n a 1/2^(n+1) i quadrati gia'
contenuti nel cerchio si dividono in quattro, e si
aggiungono alcuni quarti di quelli che prima attraversavano la
circonferenza), e' limitata superiormente
da 4 (il quadrato di lato 2 contiene il cerchio) quindi converge.9-10-08 lezione 3 (Tortorelli): Riallaccio alla precedente lezione, ordini di grandezza, calcolo approssimato e convenzioni relative, propagazione degli errori.
Riferimenti :[EB] cap 1.12-14 pagg. 22-26, [MA1] cap 1 pagg. 3-6, 10-13, 13-15, 19-22, [VV] cap. 1 pagg. 1-13.
- Partendo dagli esempi numeri delle successioni che approssimano per definizione la costante di Nepero ( (1+ 1/n )^n < e < (1+ 1/n )^n+1) e dell'algoritmo di bisezione per il calcolo della radice quadrata di 2 si sono introdotte le nozioni di:
intervallo di incertezza= intervallo con estremi le due stime della grandezz in oggetto,
valor (medio) stimato= punto medio di tale intervallo,
errore (massimo) relativo= semiampiezza dell'intervallo di incertezza.
-La nozione di ordine di grandezza rispetto ad una scala:
se a> o = b>0
si dice che a ha ordine di grandezza maggiore di b (per la scala delle potenze intere di 10) se
1 < o = a/b < 10
e notazione scientifica (decimale) per x:
x= y 10^k con y numero reale per cui 1 <o= y < 10, e k numero intero
(y puo' essere anche maggiore di 9)
- Esame di alcune convenzioni di scrittura approssimata (per numeri non negativi) introducendo le nozioni di:
approssimazione per difetto o troncamento
approssimazione per eccesso
arrotondamento
cifre significative= cifre non alterate dall'errore (relativamente al metodo di approssimazione o alle stime a disposizione)
cifre indicative = la prima o la seconda cifra dopo quelle significative (ordine di grandezza dell'errore)
mettendo in risalto che nella presentazione di un dato, in maniera prudenziale, si mette in evidenza l'ordine di grandezza dell'errore assoluto approssimandolo per eccesso.
-propagazione dell'errore (massimo assoluto) per somma, differenza.
10-10-08 esercitazione 2 (Mauro)materiale esercizi di calcolo approssimato di radici di polinomi e diseguaglianze.
13-10-08 lezione 4 (Tortorelli) Precisazioni sulla precedente lezione:
- dare una stima bilatera di un numero x come a < o= x < o = b vuol dire avere un incertezza pari a b-a.
-scrivere le sole cifre significative di un numero x, per la convenzione adottata nel corso
(le cifre che non vengono modificate sommando dall'errore)
significa approssimare il numero per difetto con le sole cifre significative,
e per eccesso, con diseguaglianza stretta, aumentando l'ultima cifra di 1.
- per un numero x che sia una mantissa cioe' 1< o = x < 10 , valutato con errore e di ordine di grandezza minore , si ha
numero delle cifre significative < log10 1/ (2e)
cioe' il numero di cifre significative e' il piu' grande intero strettamente minore di log10 1/ (2e).
Propagazione dell'errore per il prodotto, il reciproco e il quoziente
(per il quoziente si sono lasciati gli esempi e gli enunciati alla lettura degli studenti su [MA1] cap. 1 pagg.24-25).
Errore relativo.
Rapporti: tassi, medie, frequenze, percentuali.
Confronto relativo tra due grandezze.
Proprieta' della media aritmetica. Relazioni tra media armonica, geometrica ed aritmetica.
Media pesata. Percentuali rispetto a ... .
Prima parte dell' introduzione alle notazioni insiemistiche.
Riferimenti: [EB] cap. 1 pagg. 4-7 e 14-17, cap.2 pagg. 36-40;
[VV] cap. 1 pagg. 5-8, cap. 10 pagg. 209-213;
[MA1] cap. 1 pagg. 16-29, cap. 2 pagg. 44-50 (da rileggere in seguito), cap.3 pagg. 113 -117, cap. 4.3 pagg.145-146 ;
[BDM] cap. 1 pagg. 11-17, cap. 1.5 pagg. 42-47, pagg. 72-74 Es. 2.22-23-24-25 (da rileggere in seguito);
[PB1] cap.1 pagg. 1-3, pagg.6-7 e pag. 9.
Notazioni: notazioni per appartenenza, insieme vuoto, inclusione, {x}, {x,y}, ...
Definizioni:. errore relativo, frequenza assoluta, frequenza relativa (vera frequenza), media aritmetica, media pesata, media geometrica, media armonica, insieme vuoto, insieme delle parti, inclusione, specificazione, rimpiazzamento
Enunciati: - se si valutano 0<v-e <o= x <o= v+e, 0<w-E <o= y <o= w+E e gli errori relativi sono non piu' grandi di 1/10 allora Ee ha ordine di grandezza minore sia di Evche di ew ed entrambi hanno ordine di grandezza minore di vw.
Se poi la somma degli errori relativi e' piu' piccola di 1/10 allora anche Ev+ew ha ordine di grandezza minore di vw.
Se la somma degli errori relativi e del loro prodotto e' piu' piccola di 1/10 anche Ev+ew+eE
ha ordine di grandezza minore di vw.
(dimostrazione prima parte: bisogna confrontare potenze di 10 quindi va tutto scritto mettendo in risalto tali potenze: v=a 10^h, w=b 10^k con notazione scientifica,
mentre gli errori si scrivano mettendoli in relazione agli esponenti gia' scritti
e=c 10^h-1,E=d 10^k-1. , ed avendo ragionevolmente assunto gli errori piu' piccoli delle valutazioni c e d sono minori di 10.
Le ipotesi e/v < o= 1/10, E/w <o= 1/10 si traducono in
c <o= a, d <o= b.
Ora si trascrivano con questa notazione le quantita' da confrontare
vw = ab 10^h+k
eE = cd 10^h+k -2
ew = cb 10^h+k -1
vE = ad 10^h+k -1
se eE avesse ordine di grandezza h+k-1 vorrebbe dire cd >o= 10 (non puo' aumentare di piu' perche' c e d son minori di 10)
nel caso pero' essendo tutti numeri positivi ab >o= ad, cb >o= cd tutti i prodotti sarebbero maggiori di 10, e quindi anche le altre quantita' avrebbero un ordine di grandezza in piu' rispetto gli esponenti).
- L'errore relativo della valutazione del reciproco e' uguale all'errore relativo della valutazione iniziale.
- La media aritmetica M di n numeri x1, ... , xn e' il numero x che rende minima la quantita'
Q=1/n[(x-x1)^2 + ... + (x-xn)^2 ]
quantita' che amplifica le distanze maggiori di 1 dai numeri dati e smorza quelle minori di 1.
In effetti sviluppando i singoli quadrati e mettendo in evidenza le potenze di x
Q= x^2 -2x M + x1^2+...+xn^2
Quindi render minimo Q vuol dire render minimo x^2-2xM = (x-M)^2 -M^2
ma il valore minimo di un quadrato e' 0 e cio' accade nel caso per x=M.
-Se n entita' rispettivamente nei tempi t1 ... , tn producono un'unita' di una certa sostanza il tempo di produzione della quantita' media prodotta di sostanza e' la media armonica dei numeri t1 ... , tn .
- Dati dei numeri positivi non nulli si ha:
Media armonica < o= Media geometrica < o= Media aritmetica
(Per il caso di due numeri x^2 e y^2 > 0 si ha (x-y)^2 >o= 0 e quindi x^2+y^2 >o= 2xy
quindi la media aritmetica di x^2 e y^2 non e' minore della loro media geometrica.
Scrivendo la media geometrica come reciproco della media geometrica dei reciproci si ottiene l'altra diseguaglianza).
-Prime regole di formazione degli insiemi (rispecchiano fatti intuitivi)
1- due insiemi sono eguali se e solo se sono uno incluso nell'altro e viceversa
(ovvero hanno esattamente gli stessi elementi)
(estensionalita')
2- c'e' l'insieme vuoto
3- dato un insieme A c'e' il sottoinsieme dei suoi elementi che soddisfano una data proprieta' Q
(regola di formazione di sottoinsiemi per specificazione) tale sottoinsieme viene denotato con la scrittura
{x elementi di A : Q (e' vera) per x}
4- se ad ogni elemento i di un insieme I associo un elemento Ai c'e' l'insieme costituito da tutti, e solamente questi, questi Ai
(regola di formazione per rimpiazzamento) tale insieme viene denotato con la scrittura
{ Ai : (con ) i elemento di I}
5- dato un insieme A c'e' l'insieme dei suoi sottoinsiemi P(A)
(insieme delle parti di A o insieme potenza di A)
6- ci sono gli insiemi N, Z,Q, R, ...
Per esempio la proprieta' essere eguali o a 1 o a 2 o a 3 specifica il sottoinsieme di numeri che ha come elementi solo questi tre numeri e si scrive {1,2,3}.
Per esempio se A= N e per n in N considero Tn= {0,1,..., n} vi e' per rimpiazzamento l'insieme
che con notazione intuitiva possiamo denotare con {{0}, {0,1}, {0,1,2} ...}.
- Si ha che x e' elemento di {x}, l'insieme che come unico elemento ha x, ma non e' detto sia eguale a lui.
-L'insieme potenza di un insieme con n elementi ha 2^n elementi (verifica per n=3).
16-10-08 lezione 5 (Tortorelli) SOSPENSIONE DELLA DIDATTICA DI FACOLTA'.
17-10-08 esercitazione 3 (Mauro) SOSPENSIONE DELLA DIDATTICA DI FACOLTA'.
16-10-08 lezione 6 (Tortorelli)SOSPENSIONE DELLA DIDATTICA DI FACOLTA'.
23-10-08 lezione 7 (Tortorelli) Ripresentazione delle regole di formazione di insiemi enunciate ed esemplificate nella precedente lezione e continuazione dell'enunciazione delle regole di formazione di insiemi e notazioni correlate: unione, intersezione, differenza, complementare, differnza simmetrica, prodotti insiemistici.
Riferimenti: [EB] cap.2 pagg. 40-45;
[MA1] cap. 1 pagg. 28-30 ;
[BDM] cap. 1 pagg. 18-22.
Notazioni e definizioni: coppie, terne ordinate, (a,b)=(c,d) vuol dire a=c e b=d, notazioni per unioni finite, intersezioni finite, prodotti finiti di insiemi, differenza, complementare, unioni infinite, intersezioni infinite, prodotti infiniti di insiemi.
Enunciati: - l'unione e l'intersezione tra due insiemi sono commutative ed associative, e sono distributive una rispetto all'altra;
-l'unione ha come elemento neutro l'insieme vuoto, che e' annullatore nell'intersezione;
- l'intersezione di sottoinsiemi di in dato insieme ambiente X ha come elemento neutro X;
-intersezione ed unione sono idempotenti
-Leggi di De Morgan: il complemento di un intersezione e' l'unione dei complementi, il complemento di una unione e' l'intersezione dei complementi.
7- Dato un insieme A vi e' l'insieme unione su A che ha come soli elementi gli elementi di elementi di A: {x: per qualche a elemento di A, x e' elemento di a}
se per esempio A={Ai : i in I} l'unione e' Ui in I Ai ={x: per qualche i in I , x e' elemento di Ai}
8- Dato {Ai : i in I} vi e' l'insieme prodotto e non e' vuoto
Xi in I Ai = {x: x corrispondenza tra I e Ui in I Ai per cui xi sta in Ai}
24-10-08 esercitazione 4 (Mauro) diseguaglianze con moduli, radici, logaritmi.
27-10-08 lezione 8 (Tortorelli)
i- Calcolo proposizionale e quantificatori, relazioni con le notazioni insiemistiche.
ii- Coordinate cartesiane nel piano e nello spazio prima parte:.
Riferimenti: i- [EB] cap.2 pagg. 45-58, ii- [EB] cap.14 pagg. 495-498;
i- [MA1] cap. 1 pagg. 31-33, ii- [MA1] cap. 3 pagg. 97-101, pagg. 102- 106 da rileggere;
ii-[BDM] cap. 1 pagg. 51-54, cap 2 pagg. 59-74;
ii- [IRS] cap. 5 pagg. 165-168;
ii- [VV] cap. 5 pagg.75-77.
Notazioni e definizioni: i- tavole di verita', congiunzione logica, disgiunzione logica, negazione, implicazione, equivalenza logica, quantificatore universale (per ogni):
per ogni x( se p(x) allora q(x))
forme abbreviate:
per ogni x in A x(x)
sta per
per ogni x (se x sta in A allora q(x))
che si abbrevia ulteriormente se il contesto A si sottointende con
per ogni x q(x),
quantificatore esistenziale (esiste):
esiste x p(x)
forma abbreviata
esiste x in A p(x)
sta per
esiste x (x sta in A e p(x)).
ii- somma di vettori e prodotto di un vettore per un numero,
identificazione somma e prodotto per numeri di coppie e terne ordinate, sistema di riferimento, assi coordinati, base, coordinate, sistema di riferimento ortonormale o cartesiano, distanza (euclidea) tra coppie e terne:
dist((a,b), (x,y))= radice quadrata( (a-x)^2 + (b-y)^2)
norma di una coppia, terna, ... di numeri reali = distanza dall'origine
|(x,y,z)| = radice quadrata( x^2+y^2+z^2);
R, R^2,R^3 , R^n, spazio vettoriale su R,
piani coordinati e proiezioni cartesiane su di essi;
famiglia di vettori linearmente indipendenti.
Enunciati: i- corrispondenza tra operatori logici e operazioni insiemistiche, leggi di De Morgan per le operazioni logiche: non (p e q) = (non p) o (non q), non(p o q) = (non p) e (non q),
non (per ogni x vale p(x)) = esiste x per cui (non p(x)),
non(esiste x per cui p(x))= per ogni x(non p(x)).
ii- regola del parallelogramma per la somma di vettori,
la somma con un dato vettore geometricamente rappresenta una traslazione,
il prodotto di un vettore per un dato numero reale non negativo rappresenta una dilatazione con quel fattore,
il prodotto per -1 rappresenta la simmetria rispetto all'origine,
la distanza euclidea soddisfa le seguenti proprieta' generali:
dist(P,Q) > o = 0, e dist(P,Q)=0 solo se P=Q
dist(P, Q) =dist(Q,P)
dist(P,Q) < o = dist (P,R) + dist (R , P)
inoltre soddisfa
dist(r P, r Q)= |r| dist (P, Q) se r e' un numero (teorema di Talete)
dist(P+V, Q+V)= dist (P,Q) se V e' un vettore (invarianza per translazioni).
Nel piano due vettori sono lienarmente dipendenti se e solo se sono allineati con l'origine.
28-10-08 esercitazione 5 recupero (Mauro) diseguaglianze con esponenziali e logaritmi e percentuali.
29-10-08 lezione 9 recupero (Tortorelli) Riassunto della precedente lezione.
Coordinate cartesiane nel piano e nello spazio seconda parte: spazi vettoriali, dipendenza lineare,
forma parametrica di rette e piani, passaggio da una retta in forma parametrica nel piano ad una retta come luogo di zeri
Riferimenti: [EB] cap.3 pagg. 59-65, [EB] cap.14 pagg. 495-498;
[MA1] cap. 3 pagg. 97-101, pagg. 102- 106 da rileggere, [MA2] cap. 10.1, cap 10.3, cap. 10 pagg. 553-555;
[BDM] cap 2 pagg. 59-74;
[IRS] cap. 5 pagg. 171-173;
[VV] cap. 5 pagg. 77-81.
Gli argomenti trattati in questa lezione non coinvolgono la nozione di distanza ma solo quelle di traslazione, dilatazione e parallelismo
Definizioni: - Uno spazio vettoriale su R e' un insieme V con due operazioni
v+w in V se v e w sono in V (traslazione di v con w)
tv in V se v in V e t in R (dilatazione di fattore t di v).
la somma e' commutativa associativa ha elemento neutro 0V (origine) e opposto -v per ogni elemento v di V (v+(-v)=0V ), il prodotto per numeri e' distributivo rispetto alla somma
((-1)v=-v, 0v=0V).
-Un sottospazio vettoriale di V e' un suo sottoinsieme che e' uno spazio vettoriale con le stesse operazioni e la stessa origine.
- Combinazione lineare di elementi di un sottoinsieme A di uno sp.vett. V e' una somma finita del tipo t_1 a_1 + ...t_k a_k con coefficienti t_1 ...t_k in R e a_1 ... a_k in A
-L'insieme delle combinazioni lineari di elementi di A si dice sottospazio vettoriale generato da A.
i sottospazi vettoriali del piano sono: l'insieme formato solo dall'origine, le rette passanti per l'origine, il piano stesso;
i sottospazi vettoriali dello spazio sono: l'insieme formato solo dall'origine, le rette per l'origine, i piani per l'origine, lo spazio stesso.
- Un sottoinsieme A si dice di vettori linearmenti indipendenti se ogni combinazione lineare di elementi di A nulla (= 0V ) ha coefficienti numeri reali tutti nulli.
- Dei vettori di V sono linearmenti dipendenti se uno di essi sta nel sottospazio generato dai rimanenti.
- Una base di V e' per definizione un sottoinsieme di vettori di V che:
1- siano linearmente indipendenti
2- generino tutto V
-Il numero di elementi di una base di uno spazio vettoriale si dice dimensione dello spazio vettoriale.
-Dati v_1 ... v_k in V linearmente indipendenti, e P in V si dice piano k dimensionale passante per P e parallelo a (o anche ``con giacitura'') v_1 ... v_k l'insieme
{P + t_1 v_1 + ...t_k v_k: t_1 , ... ,t_k in R }
-Rette in forma parametrica e come luogo di zeri in R^2.
Problematica: come riconoscere dalle coordinate in una dato sistema di riferimento se due o piu' vettori sono o meno linearmente indipendenti, o vvero se dei punti sono allineati o complanari?
Enunciati ed esempi: - R, R^2,R^3,R^n sono spazi vettoriali con le operazioni di somma per componenti e prodotto per numero reale delle componenti;
-L'insieme delle combinazioni lineari di elementi di un sottoinsieme A di V e' un sottospazio vettoriale;
- Ogni elemento di V si scrive in modo unico come combinazione lineare degli elementi di una base di V (ogni deriva dal fatto che la base genera tutto lo spazio, l'unicita' dei coefficienti e' dovuta al fatto che una base e' linearmente indipendente)
-TEOREMA: Tutte le basi di uno spazio vettoriale hanno lo stesso numero di elementi.
- Fissata una base in uno spazio vettoriale di dimenzione finita n esso si identifica con R^n :
infatti si identificano mettendoli in ordine gli elementi della base v_1 ... v_n rispettivamente con
(1,0 ... 0), (0,1,0 ...), .... , (0,... 0 ,1) ,
quindi v = t_1 v_1 + ...t_n v_n si identifica con t_1 (1,0 ... 0) + ...+t_n (0 ... ,1)=(t_1, t_2 ... t_n).
-Lo spazio vettoriale dei polinomi con coefficienti reali e' di dimensione infinita.
-Se un piano di dimensione k passa per l'origine e' un sottospazio vettoriale, tutti i piani sono traslati di sottospazi vettoriali, se traslo un sottospazio per un suo elemento ottengo lo stesso sottospazio.
- Rette in R^2 in forma parametrica: esempio numerico.
In generale la retta per P (punto di partenza) di coordinate (a,b) parallela a v (velocita') di coordinate (p,q) e' l'insieme
{(a+tp, b+tq) : t in R}
gli (x,y) in R^2 che stanno su tale retta sono quelli per cui vi e' t in R tale che (x,y)=(a+tp, b+tq)
cioe'
-------------------------------------------------------------- a + t p = x
gli (x,y) per cui vi e' soluzione t in al sistema
-------------------------------------------------------------- b + t q = y
moltiplicando la prima equazione per q la seconda per p e sottraendole si ottiene che
gli (x,y) che stanno sulla retta soddisfano l'equazione qx - py + pb - qa = 0
Quindi
{(a+tp, b+tq) : t in R} = {(x,y) in R^2 : qx - py + pb - qa = 0 }.
- Ogni retta si scrive come luogo di zeri {(x,y): Ax+By+C=0}.
- Due vettori in R^2 v=(p,q) e w=(h,k) sono paralleli, ovvero visti come punti sono allineati con l'origine se e solo se
pk - qh = 0
(infatti perche' lo siano uno dev'essere multiplo dell'altro quindi vi deve essere t in R per cui
p=th e q=tk, a parte il caso degenere in cui uno dei vettori e' nullo, dividendo si ottiene l'eliminazione di t e l'eguaglianza p/q= h/k).
30-10-08 lezione 10 (Tortorelli) Riassunto della precedente lezione.
Coordinate cartesiane nel piano e nello spazio terza parte. Si affronta il seguente tipo di problema: quali equazioni devono soddisfare le coordinate di vettori perche' siano linearmente dipendenti? Quali equazioni devono soddisfare le coordinate di un punto perche' stia su un piano o su una retta di data giacitura? Determinanti e loro interpretazione geometrica.
Riferimenti: [EB] cap.14 pagg. 475-479 , pagg. 511-517, 521-525;
[MA2] cap. 10.3, cap 10.4, cap.10 pagg. 549-553, cap 10.8 pagg. 578-583;
[BDM] cap 2 pagg. 92-97, cap. 3 pagg. 101-103, 110, 112-113, 124-129;
[IRS] cap. 5 pagg. 186-190, 201, 5.9.4 pagg. 206-208;
[VV] cap. 4 pagg. 70-73.
Definizioni e notazioni: - Coefficiente angolare di una retta nel piano, tasso di variazione o rapporto incrementale, pendenza di una retta nel piano, matrice con h righe e k colonne e notazioni correlate, matrice per colonne delle coordinate e matrice per righe delle coordinate, matrice trasposta,determinante di una matrice quadrata sviluppato secondo la prima colonna:
det matrice di prima colonna (p,q) e seconda (h, k)= pk-qh
det matrice di prima colonna (x,y,z) seconda (p,q,r) e terza (h,k,j)=
x(qj-kr) - y(pj -hr) + z( pk-hq)
det matrice di colonne M^1 ... M^n =
M^1_1 det (della matrice senza la prima colonna e la prima riga) +
- M^1_2 det (della matrice senza la prima colonna e la seconda riga) +
...
(-1)^(1+i) M^1_i det (della matrice senza la prima colonna e le i-esima riga) +
...
Prodotto vettore di v=(p,q,r) e w=(h,k,j): vxw= (qj-kr, - (pj -hr), pk-hq)
e' dato dalla terna di determinanti delle matrici due per due della matrice delle coordinate dei due vettori,
ovvero e' la terna delle aree a segno alterno dei tre parallelogrammi ottenuti proiettando cartesianamente sui tre piani coordinati (ordinati come il vettore di base da ciascuno escluso) il parallelogramma di vertici 0, v, w, v+w.
Una base e' equiorientata con la base canonica di R^n se il determinante della matrice delle coordinate dei vettori e' positivo.
Equazione generale di un piano nello spazio
{(x,y,z): Ax +By+Cz+D=0},
sistema di equazioni generale di una retta nello spazio
{(x,y,z) : Ax+By+Cz +D=0 e ax+by+cz +d=0}
(quando (A,B,C) e (a,b,c) siano non allineati con (0,0,0))
Enunciati: - Il tasso di variazione incrementale e' costante su rette parallele,
- L'orientazione e' un concetto relativo (come quello di percentuale)
- A livello intuitiuvo l'area orientata A(v,w) di un parallelogramma di vertici (0,0), v, w e v+w soddisfa
1) A(v,w) = -A(w,v) (definizione di area orientata),
2) A(tv, w) = tA(v,w) per t in R,
3) A(v+tw, w) = A(v,w)
4) A((1,0), (0,1)) = 1
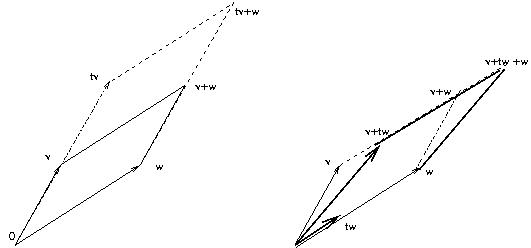
- Da 1), 2), 3) segue
3 bis) A(v+V,w) = A(v,w) +A(V,w)
(infatti: se v e w sono dipendenti v=sw e quindi da 3) A(sw+V,w)= A(V,w) = sA(w,w)+ A(V,w) da 1); se invece v e w sono indipendenti sono una base e quindi V=sv +tw e si usano
3) 2) da sinistra a destra e poi da destra a sinistra)
- TEOREMA 1 sul determinante:
Vi e' un solo modo di associare ad una matrice M n per n un numero A(M) in modo che
1) se N e' ottenuta da M scambiando di posto due colonne: A(M) = - A(N)
2) se N e' ottenuta da M moltiplicando una colonna per t in R: A(N) = t A(M)
3bis) A(M^1 +V, M^2 ... ) = A(M) + A(V, M^2, ... )
4) se M e' fatta con 1 sulla diagonale discendente e 0 altrove : A(M)= 1
- TEOREMA 1 bis sul determinante: sviluppo per colonne del determinante
Nel caso 2 per due si procede come segue
A((p,q),(h,k))= A( p(1,0) + q(0,1), (h, k))= [3 bis) e 2)] pA((1,0), (h,k)) +qA((0,1), (h,k)) =
pA((1,0), h(1,0)+ k(0,1)) +qA((0,1), h(1,0)+ k(0,1)) = [su ogni addendo1), 2), 3 bis) e ancora1)]
phA((1,0),(1,0)) + pkA((1,0),(0,1)) + qhA((0,1),(1,0)) + qkA((0,1),(0,1)) = [per 1 A(v,v)=0]
pkA((1,0),(0,1)) + qhA((0,1),(1,0)) =[1)] (pk - qh)A((1,0),(0,1))= [4)] pk - qh.
-Il determinante si puo' pensare come ``volume orientato di dimensione n'' del ``parallelepipedo di dimensione n'' di vertici l'origine i vettori colonna e le loro somme.
- TEOREMA 2 sul determinante: il determinante di una matrice e' eguale a quello della sua trasposta.
- TEOREMA 3 sul determinante: n vettori in R^n sono linearmente dipendenti se e solo se il determinante della matrice delle loro coordinate e' nullo.
In particolare un punto X=(x,y,z) sta nel piano {P+ tv+s w: t ed s in R} con P=(a,b,c), v=(p,q,r), w=(h,k,j) e v, w linearmente indipendenti se e solo se X-P dipende linearmente da v e w
cioe' sta nello sottospazio vettoriale generato da v e w (che al piu' e' un piano per l'origine)
se solo se il parallelepipedo di vertici (0,0,0), X-P, v, w, X-P+v+w e' degenere (piatto) e quindi ha volume nullo:
det (X-P, v, w)=0: ovvero
{P+ tv+s w: t ed s in R} ={(x,y,z): x(qj-kr) - y(pj -hr) + z( pk-hq) - det (P,v,w)=0}
-TEOREMA 3 bis sul determinante: k vettori in R^n, n>k, sono linearmente dipendenti se e solo se tutti i determinanti delle sottomatrici k per k della matrice delle loro coordinate sono nulli.
Ovvero se le loro proiezioni cartesiane sui sottospazi coordinati di dimensione k sono linearmente dipendenti.
OSSERVAZIONE AGGIUNTA: in realta' le condizioni possono essere in numero minore.
In particolare un punto X=(x,y,z) sta sulla retta non degenere {tv: t in R}, v=(p,q,r) non nullo,
quando due opportune tra le tre sottomatrici 2 per 2 della matrice di colonne (x,y,z) e (p,q,r) hanno determinante nullo (nel caso la terza sottomatrice avra' anch'essa determinante nullo).
Infatti trattando il caso in cui v e' diverso da (0,0,0) si puo' supporre q non 0:
se (x,y)=t (p,q) (determinante prima sottomatrice nullo) e (y,z)=s(q,r) (determinante seconda sottomatrice nullo) allora y=tq=sq quindi
s=t per cui (x,z)=t(p,r) (determinante terza sottomatrice nullo).
Quindi si ha se v=(p,q,r) non e' (0,0,0)
{tv :t in R} = {(x,y,z): qx-py = 0 e ry-qz = 0} se q non 0
{tv :t in R} = {(x,y,z): ry-qz = 0 e rx-pz = 0} se r non 0
{tv :t in R} = {(x,y,z): qx-py = 0 e rx-pz = 0} se p non 0
{tv :t in R} = intersezione di due piani non coincidenti.
31-10-08 esercitazione 6 (Mauro) esercizi su successioni crescenti decrescenti, limitate e limiti di
semplici successioni razionali; alcuni sottoinsiemi del piano cartesiano definiti con diseguaglianze; cambiamenti di base e determinanti nel piano.
3-11-08 lezione 11 (Tortorelli) Spiegazioni in margine alla precedente lezione: rette come intersezione di piani non paralleli.
Misure angolari definizioni e proprieta' di trigonometria piana, espressione in coordinate delle grandezze trigonometriche: il prodotto scalare. Ortogonalita' prodotto vettore e determinante,
sistemi, rette e piani, formula di Cauchy-Crofton-Pitagora.
Riferimenti: [EB] cap.5 pagg. 110-132 (lettura consigliata pagg. 133-139) , pagg. 498-511;
[MA1] cap. 4.10 pagg. 201-203, 206-211,
[MA2] cap. 5.5 pagg. 256-259, 261-269, cap. 10.2, cap 10.3, cap.10 pagg. 549-553;
[BDM] cap 2 pagg. 75-91;
[IRS] cap. 5 pagg. 168-180;
[VV] cap. 6.4 pagg. 119-121, 123.
Definizioni: distanza , norma in R^n e sue proprieta', circonferenze e sfere come luoghi di zeri, grandezze trigonometriche:
se x e' tra 0 e pigreco:
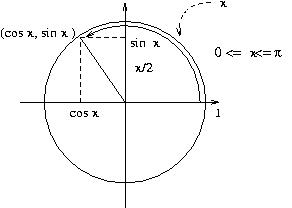
(cos x, sin x) sono le coordinate del secondo estremo Q dell'arco,
a partire da P(1,0) sulla circonferenza unitaria di centro l'origine
in modo che det(PQ)>0 (i.e. percorso in senso antiorario),
che sottende un settore di area x/2 (di lunghezza x)
se x e' tra -pigreco e 0: cos x=cos (-x), sin x=-sin(-x)
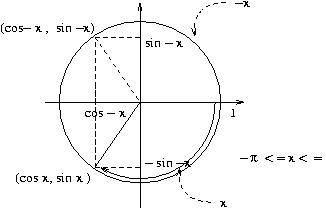
per gli altri x in R :
sia k in Z per cui -pigreco <=o x - 2kpigreco <o= -pigreco
cos x =cos (x- 2kpigreco), sin x =sin (x- 2kpigreco)
Definizione di tangente: tan x = sin x / cos x
per x diverso da pigreco/2 + k pigreco per tutti i k in Z .
si ha dalla definizione geometrica tan x = tan ( x + k pigreco) per tutti i k in Z .
Norma Euclidea: |v| = distanza dall'origine = radice della somma dei quadrati delle coordinate
Prodotto scalare: v=(x_1, ... , x_n), w=(y_1, ... , y_n), v.w = x_1y_1 + ... + x_ny_n
somma delle coordinatedi stesso posto
Enunciati: formule trigonometriche PDF ,
se a^2 +b^2= 1 allora vi e' x per cui a =cos x , b = sin x
si ha sempre -1 < o = cos x <o= 1 e -1 < o = cos x <o= 1
Dimostrazione formule di addizione:
cos (x+y)=cos x cos y - sin x sin y, sin (x+y)= sinx cos y+cos x sin y

sin (x+y)=(sin y + z sin x) cos x = sin y cos + z cos x sin x = sin y cos x + cos y sin x.
Formule di seno e coseno in termini della tangente di meta' arco: dimostarzione con formule di addizione.
Proprieta' del prodotto scalare
Problema: esprimere mediante le coordinate le grandezze trigonometriche
il coseno dell'angolo tra due vettori non nulli di R^n e' il rapporto tra loro prodotto scalare e prodotto delle loro norme
il seno dell'angolo orientato tra due vettori di R^2 non nulli e' il rapporto tra determinante della matrice delle loro colonne e il prodotto delle loro norme
Il determinante di una matrice 3x3 e' il prodotto scalare della prima colonna con il prodotto vettore della seconda con la terza: e' quindi il seno dell'angolo primo vettore colonna con il piano formato dagli ultimi per il seno dell'angolo orientato tra secondo e terzo vettore colonna per il prodotto delle tre norme
Le equazioni che devono soddisfare le coordinate di un punto per stare su un piano o su una retta sono condizioni di ortogonalita'
Come trovare la giacitura di un piano dato come luogo di zeri
I sistemi lineari sono condizioni di ortogonalita'
Formule di Cauchy Crofton Pitagora per l'area di un parellelo gramma nello spazio tridimensionale.
3-11-08 Prima prova in itinere (Tortorelli Mauro)
5-11-08 Soluzione pubblica dei temi della prima prova in itinere (Tortorelli - Mauro)
prossima pubblicazione nel sito del corso.
6-11-08 lezione 12 (Tortorelli) Proprieta' del prodotto scalare.
Esempi ed ed esercizi relativi alla precedente lezione:
calcolo di prodotti vettori nello spazio, distanza di un punto da una retta data in forma parametrica, calcolo della direzione di una retta data come intersezione di due piani
con la risoluzione di un sistema e con il prodotto vettore deglle direzioni ortogonali ai due piani, distanza di un punto da una retta.
Notazione matriciale per i sistemi e due interpretazioni per i sistemi e per le matrici:
-coefficienti di una combinazione lineare di vettori colonna che deve dare un vettore dato;
-coordinate di punti che devono soddisfare certe condizioni di ortogonalita' con i vettori riga;
Cambiamenti di base iterati: prodotto riga per colonna di matrici e sue proprieta'.
Trasformazioni lineari e terza interpretazione delle matrici e dei sistemi.
Le due nozioni principali sono quelle di prodotto riga per colonna e di trasformazione lineare.
Anticipiamo sottolineandola quest'ultima nozione.
Una trasformazione T tra due spazi vettoriali V e W si dice lineare se
T(0V) = 0W ,
T(v+z) = T(v) + T(z) , per v e z in V,
T(tv) = t T(v), per v in V e t in R,
La matrice associata ad una trasformazione lineare e' la matrice che ha come colonne le coordinate dei trasformati dei vettori della base canonica.
Prodotto righe per colonne di matrici come iterazione di trasformazioni lineari.
Matrici di rotazioni piane intorno all'origine.
Riferimenti: [EB] cap.14.2 pagg. 477 -495, pagg. 517-520;
[MA2] cap. 10.4, cap 10.3, cap.10.7 pagg. 570-578 cap. 10.8 pagg. 584-585;
[BDM] cap 3 pagg. 104-113, 114-120, 120-124;
[IRS] cap. 5 pagg. 188-199, 200-205;
[VV] cap. 4 pag. 73-74.
Definizioni: ricordando che per una matrice M si indica con M_i^j il coefficiente che sta nella i-esima riga dall'alto e nella j-esima colonna da sinistra, il prodotto righe per colonne tra una matrice
B=(B_i^j ), 1 <o= i <o= n e 1<o= j <o= k con n righe e k colonne
e una matrice
A= (A_i^j ), 1 <o= i <o= k e 1<o= j <o= m, con k righe ed m colonne
e' un matrice
C=(C_i^j ), 1 <o= i <o= n e 1<o= j <o= m con n righe e m colonne
per cui C_i^j = B_i . A^j = B_i^1 A_1^j + B_i^2 A_2^j + .... + B_i^k A_k^j.
****************************** a b ************ A B **********
Per esempio la matrice *********** * per la matrice * e': *
****************************** c d ************ C D **********
aA +bC aB+bD
*
cA+dC cB+dD
Una matrice riga per una matrice colonna e' il prodotto scalare delle coordinate.
Somma di matrici (di egual dimensione) e prodotto per un numero.
Matrice identica, matrice inversa di una matrice quadrata.
Trasformazioni lineari e matrici ad esse associate.
Rotazioni attorno l'origine nel piano.
ESERCIZIO : a quale matrice e' associata la riflessione rispetto ad una retta passante per l'origine.
Enunciati: proprieta' del prodotto scalare
1) v . v >o = 0 e v . v = 0 se e solo se v= 0 ;
2) v . w = w . v ;
3) (v+t W) . w = v . w + t( W . w),
v . (w +t V) = v . w + t(v . V);
4) v . v = || v||^2 ;
5) |v . w | < o = ||v|| ||w|| , e vale l'eguaglianza se e solo se v=s w (diseguaglianza di Cauchy-Schwartz)
Si noti che con queste proprieta' molti calcoli possono essre affrontati senza sviluppare effettivamente con le coordinate i prodotti scalari, per esempio:
|| v-w||^2 = (v-w) . (v - w) = v . v + w . w - v . w - w . v =
= ||v||^2 + || w||^2 - 2 v . w
- La matrcie associata a due cambiamenti di base consecutivi e' il prodotto righe per colonne della matrice A con colonne le coordinate nella prima base dei vettori della base canonica, seguita da quella B che ha come colonne le coordinate nella seconda base dei vettori della prima:
se infatti consideriamo E_i il vettore colonna della bae coordinata (0,... 0,1,0 ...0), ove 1 compare solo al posto i-esimo:
B(A E_i) = B A^i = vettore colonna di coordinate B_1 . A^i .... B_n . A^i
= i-esimo vettore colonna di BA = (BA)E_i
e quindi per ogni vettore colonna X: B(AX)= (BA)X
Proprieta' del prodotto righe per colonne:
- distributivita' a destra e a sinistra C(A+B)= CA+CB, (A+B)D= AD +BD
- associativita' (AB)C=A(BC)
- t(AB)=(tA)B=A(tB)
- elemento neutro : la matrice I con colonne le coordinate della base canonica , con tutti 0 tranne 1 solo sulla diagonale che scende da sinistra e' tale che per ogni altra A matrice quadrata di egual dimensione si ha
AI= IA = A
Si osserva che det I =1
NOTA: attenzione anche per matrici quadrate non e' vera la proprieta' commutativa del prodotto righe per colonne BA e' in generale diverso da AB
TEOREMA 4 sul determinante: date due matrici quadrate di egual dimensioni
det (AB) = det A det B
questa proprieta' segue direttamente dall'unicita' del determinante.
Per matrici quadrate relative a colonne indipendenti (cambiamenti di base, determinante non nullo) si ha
-per ogni matrice M di questo tipo la matrice associata al cambiamento di coordinate inverso
indicata con M^{-1} e' tale che:
M^{-1}M = MM^{-1} = I
-TEOREMA 5 sul determinante: det (M^{-1} A M ) = det A
Se T e' una trasformazione lineare le coordinate del trasformato di un vettore v
sono quelle date dal prodotto righe per colonne della matrice associata alla trasformazione e v.
Quindi una volta nota una trasformazione lineare sugli elementi della base canonica e' nota ovunque.
TEOREMA FONDAMENTALE DELL' ALGEBRA LINEARE
Tutte e sole le trasformazioni di uno spazio vettoriale di dimensione maggiore di 1per cui
(- ogni punto dello spazio e' il trasformato di qualche altro punto)
- l'origine viene lasciata fissa
- coppie di rette parallele distine sono trasformate coppie di rette parallele distinte
sono le trasformazioni lineari con inversa.
- Le soluzioni di un sistema quindi si possono interpretare come le coordinate dei vettori
che vengono trasformati, dalla trasformazione relativa alla matrice, nel vettore che ha come ccordinate i coefficienti del termine noto.
TEOREMA:
Se A e B sono le matrici associate a due trasformazioni rispettivamente S e T la matrice BA, ottenuta facendo il prodotto righe di B per colonne di A, e' quella associata alla trasformazione ottenuta prima agendo con S e quindi con T.
Basta verificarlo sugli elementi della base canonica.
il vettore j-esimo della base canonica, indicato con e_j, viene trasformato da S nel vettore che ha come coordinate quelle della j-esima colonna di A,
(A_1^j ..... A_n^j) = A_1^j e_1 + ... + A_n ^j e_n,
quindi questo da T viene trasformato in
A_1^j B^1 + ... + A_n ^j B^n
che ha come componente i-esima proprio A_1^j B_i^1 + ... + A_n ^j B_i^n.
-La matrice associata, relativamente alla base canonica, ad una rotazione in senso antiorario di angolo a radianti attorno all'origine nel piano e'
********************* cos a - sin a *****
********************* *
********************* sin a cos a *****
infatti ( cos a ,sin a ) sono le coordinatre del ruotato in senso antiorario di (1,0)
e ( -sin a , cos a ) sono le coordinate del ruotato in senso antiorario di (0,1), quindi
(x,y) ----> ( x cos a - y sin a , x sin a + y cos a )
infatti, per linearita', il ruotato e' la somma dei ruotati, e il ruotato ``dell' allungato'' e' ``l'allungato'' di egual fattore del ruotato, per cui
(x, y)= x(1,0)+ y(0,1) ----> x ( cos a ,sin a ) + y( -sin a ,cos a )
-Le trasformazioni lineari per cui vi e' la trasfomazione inversa sono esattamente quelle le cui matrici hanno determinante non nullo.
La matrice associata alla trasformazione inversa e' l'inversa della matrice associata alla prima trasformazione.
-Se si cambia sistema di coordinate con una matrice C la matrice M associata ad una trasformazione T diventa
C M C^{-1}
vecchie coordinate <-- C^{-1} <--nuove coordinate
coord. vecchie del trasformato <-- M <--vecchie coordinate
coord. nuove del trasformato <-- C <-- coord. vecchie del trasformato
si osserva che il determinante di queste due matrici e' uguale ed e' quindi associato solo alla trasformazione che esse rappresentano nei due diversi sistemi di coordinate!
Invece il prodotto scalare cambia cambiando i sistemi di coordinate mediante una matrice C con colonne indipendenti
v . w e' diverso da Cv . Cw in generale
ma se il nuovo sistema di coordinate e' cartesiano cioe' di vettori ortogonali e di lunghezza uno
si ha
v . w = Cv . Cw se le colonne di C^{-1}, (coordinate degli elementi della nuova base) , sono tra loro ortogonali e di lunghezza 1,
*************************************************************************
chiaramente e' vero il viceversa basta prendere come v e w proprio le colonne di C^{-1}
per cui la condizione e' anche equivalente a
C^{-1} p .C^{-1} q = p . q
e al fatto che le colonne di C sono ortogonali e di lunghezza 1
cioe' C^{-1}= trasposta di C.
7-11-08 esercitazione 7 (Mauro) equazioni parametriche e cartesiane delle rette nel piano, aree di parallelogrammi, inverse di matrici 2x2 e 3x3, distanza da piani, rotazioni attorno a punti, riflessioni, campi di esistenza e regioni del piano definiti da diseguaglianze.
10-11-08 lezione 13 (Tortorelli)
i- Riassunto e precisazioni su trasformazioni lineari e prodotto righe per colonne di matrici.
Matrice trasposta e formula per la matrice inversa. Matrici di riflessione per una retta passante per l'origine.
ii- La nozione astratta di funzione e quelle ad essa legati.
Si tratta di funzione quando ad ogni elemento di un insieme di dati ammissibili o interessanti si associa un solo valore.
Per questo si scrive x--->f(x) per dire che la funzione f trasforma il dato x
nel risultato f(x) ed mediante f partendo da x non si possono ottenere altri risultati.
Si scrive anche f(x)=y per indicare che quast'unico risultato e' eguale a y.
L'insieme dei dati ammissibili o interessanti si dice dominio della funzione
L'insieme dei valori di una funzione in un dominio si dice immagine. Si scrive
f:A --->B o x in A, x ---> f(x) in B
intendendo una funzione definita sugli elementi di A , che li trasfroma in elementi di B
In particolare l'immagine di A tramite f sara' un sottoinsieme di B.
Per avere un rigore maggiore si puo' ridurre il concetto di funzione a quello di
relazione binaria di tipo funzionale (vedi sotto).
Esempi:
associare ad un numero x i numeri y per cui y^2=x
non e' una funzione da numeri a numeri
infatti per prima cosa la regola non da risultato se x e' negativo,
comunque rimane l'ambiguita' se ad x associare rad.quad.|x| piuttosto che -rad. quad.|x|.
Piuttosto:
associare ad un numero non negativo x l'insieme dei numeri y per cui y^2=x
e' una funzione da numeri ad insiemi
infatti dato x >o=0 e' ben determinato solo usando x l'insieme { rad.quad.|x| , -rad. quad.|x|}
x ----->{ rad.quad.|x| , -rad. quad.|x|}
Anche:
associare ad un numero non negativo x l'unico numero non negativo y per cui y^2=x
e' una funzione da numeri a numeri
x -----> rad.quad.|x|
Considerando le seguenti espressioni
x in R, f(x)=1; x in R g(x)= (x^2+1)/(x^2+1); x in R h(x)=(1-x)/(1-x)
si osserva che f e g sono la stessa funzione (f=g) seppur calcolata in modo diverso,
mentre h e' una funzione diversa poiche' la formula data per specificare la funzione si porta dietro la condizione x non= 1, e quindi h ha un dominio diverso da f, quindi pur dando lo stesso risultato di f nella parte di dominio comune e' diversa proprio perche' ha dominio diverso.
Funzioni reali di una variabile reale.
Grafici approssimativi di
x in I , x --> x; x in R , x --> x^2; x > o = 0, x--> x^2; x >=0, x--> radice quadrata di x; x in R , x--> sin x; x tra -pigreco/2 e pigreco/2 , x--> sin x;
x in R , x--> cos x; x tra 0 e pigreco , x--> cos x;
x tra -1 e 1 , x--> arsin x; x tra -1 e 1 , x--> arcos x;
Funzioni di piu' variabili: funzioni il cui dominio e' un sottoinsieme di R^k
x in R^k quindi x=(x_1 , ... x_k) per f(x) si scrive semplicemente f(x_1, ..., x_k)
Esempi.
Funzioni vettoriali ( a valori in R^n): le si considerera' come n funzioni a valori numeri reali ordinate, ognuna da la rispettiva coordinata del punto-valore
x ---> f(x) = ( f_1(x), f_2(x) ... f_n (x))
Esempi.
Il grafico di una funzione f, reale di variabile reale, {(x,y): x=f(x)} sottoinsieme di R^2
si vede come immagine di una funzione a valori nel piano
x---> F(x)=: (x, f(x)) (percorsi , cammini),
e anche come luoghi di zeri di una funzione di due variabili
G(x,y)= y-f(x)
Riferimenti: [EB] cap. 3 pagg. 59 -78; cap. 4 pagg.90-98 pagg.101-106, cap. 14 pagg. 518-520;
[MA1] cap 3 pagg. 87-98, pagg.101-106 (da rileggere in seguito), cap. 4 pagg.125-129
pagg. 134-135, pagg. 201-206, pagg.214 -219;
[BDM] cap 4 pagg. 139-158, 164-170, 171-175, cap5. 179-192, 193, 202-212
cap. 6 pagg. 235-240;
[VV] cap. 6 pag. 91-100, 122-128.
Definizioni: i- Matrice trasposta.
ii- relazioni binarie, relazioni funzionali:
-f sottoinsieme di DXB e' di ``tipo funzione'' se
(a,b) in f e (a,c) in f ==> c=b (il risultato e' determinato in modo unico dal dato a);
se f e' di tipo funzione invece di (a, b) in f si scrive b=f(a).
- dati ammissibili o interessanti per una funzione: dominio
data f di tipo funzione come sottoinsieme di DxB essa si porta dietro il suo dominio
dom f={ x: esiste b in B per cui (x, b) in f} =
={ x: esiste b in B per cui f(x)=b }
Se si scrive f: A-->B si indende che A e' il dominio di f.
Nel caso A viene specificato a secondo dell'interesse.
- valori di una funzione: immagine di una funzione f su un dominio C
se C e' un sottoinsieme del dominio A di una funzoine f (f:A-->B)
il sottoinsime di B dato dai valori di f sugli elementi di C si dice immagine di f su C.
im_C f ={y in B: esiste x in C y=f(x)}.
-funzione composta
-funzione inversa
-restrizione:
si dice restrizione di f a C sottoinsieme del dominio di f la funzione che ha come dominio
C e come valori quelli dati da f.
-funzioni (a valori) reali di (una) variabile reale
-funzioni di piu' variabili reali
-funzioni vettoriali (in R^n)
-grafico dell'inversa
- arsin , arcos
- iniettivita' di una funzione f in un sottodominio C:
per ogni a e b in C se f(a)=f(b) allora a=b,
vuol dire: aver (eventualmente) un unica soluzione in C di f(x)=y (per le equazioni che hanno soluzioni in C);
- surgettivita' di una funzione f in un sottodominio C su un insieme B:
per ogni b in B esiste c in C f(c)=b
vuol dire: per ogni dato b in B vi e' almeno una soluzione in C di f(x)=b
-bigettivita'
Enunciati:
i -Formula per l'inversa di una matrice.
- Si e' visto che cambiando base con una matrcice C la matrice M associata ad una trasformazione T cambia e diventa CMC^{-1}.
Quindi il determinante della matrice associata ad una trasformazione non cambia cambiando base.
In generale invece il prodotto scalare cambia cambiando i sistemi di coordinate mediante una matrice C con colonne indipendenti
v . w e' diverso da Cv . Cw in generale
ma se il nuovo sistema di coordinate e' cartesiano cioe' di vettori ortogonali e di lunghezza uno
si ha
v . w = Cv . Cw se le colonne di C^{-1}, (coordinate degli elementi della nuova base) , sono tra loro ortogonali e di lunghezza 1.
(L'argomento qui di seguito riportato non e' stato svolto a lezione )
************************************************************************
Per vederlo si osserva che (CV . Cw) = ((trasC C)v .w) e se questo per ogni w e' eguale a
v .w si ha per l eproprieta' del prodotto scalare (((trasC C)v -v) .w) =0 per ogni w e quindi prendendo come w il primo fattore si ha che per ogni v il vettore (trasC C)v -v e' nullo.
Cioe' (trasC C)v =v per ogni v. Cioe'
trasC = C^{-1}
Quindi le colonne di C sono tra loro ortogonali e di lunghezza 1.
Chiaramente e' vero il viceversa basta prendere come v e w proprio le colonne di C^{-1}
per cui la condizione e' anche equivalente a
C^{-1} p .C^{-1} q = p . q
e al fatto che le colonne di C^{-1} sono ortogonali e di lunghezza 1.
*************************************************************************
-La matrice associata, relativamente alla base canonica, ad una riflessione rispetto ad una retta passante per l'origine con pendenza di a radianti e'
********************* cos 2a sin 2a *****
********************* *
********************* sin 2a - cos 2a *****
ii - un sottoinsieme del piano e' un grafico di funzione (rispetto all'asse orizzontale) se le rette verticali lo intersecano al piu' una volta
- Il dominio di una funzione (vista come insieme di coppie) e' la sua prima proiezione
l'immagine e' la sua seconda proiezione.
- Il dominio dell'inversa e' l'immagine della funzione (se la funzione e' invertibile)
L'immagine dell'inversa e' il dominio della funzione( se la funzione e' invertibile).
- L'inversa dell'inversa e' la funzione invertibile di partenza.
- Il grafico dell'inversa di una funzione reale di variabile reale si ottiene
facendo il simmetrico rispetto alla bisettrice {(x,x) : x in R} del grafico di partenza
- ``Risoluzione grafica '' di equazioni: dato il disegno di un grafico {(x, f(x)): x in C}
dato b termine noto per risolvere graficamente l'equazione f(x)=b
si tracci la retta orizzontale di quota b
le soluzioni saranno le prime coordinate dei punti del grafico che toccano la retta.
- Un funzione f:A--> B ha inversa definita su tutto B se e solo se
iniettiva in A e surgettiva da A su B
- Un grafico di funzione reale di variabile reale e' il grafico di una funzione iniettiva se le rette orizzontali lo intersecano al piu' una volta
- Un grafico di funzione reale di variabile reale e' il grafico di una funzione surgettiva su B se per ogni ``quota'' b in B le rette orizzontali di quella quota lo intersecano almeno una volta
- Restringendo x^2 a [0;+oo), sinx a [- pigreco/2 , pigreco /2] , cosx a [0 , pigreco] si ottengono funzioni bigettive sulle immagini delle funzioni iniziali
- Rette non verticali come grafici
-Grafici come immagini di funzioni vettoriali e come luoghi di zeri di funzioni di piu' variabili.
13-11-08 lezione 14 (Tortorelli)
Argomenti generali e definizioni:
Iniettivita' e surgettivita' d funzioni lineari di R^n in se, nucleo di una funzione lineare, principio di sovrapposizione;
grafico di tangente e arcotangente;
insiemi di livello, sottolivello, sopralivello, per funzioni a valori reali luoghi di zeri, sopragrafici e sottografici; coordinate polari;
grafici di funzioni lineari e affini di una variabile reale a valori reali e loro inverse;
operazioni sui grafici; f(x)+c, f(x+c), mf(x), f(mx);
grafici dei trinomi di secondo grado, delle funzioni potenza ad esponente intero e delle inverse di loro restrizioni, grafico di (ax+b)/(cx +d) .
Riferimenti: [EB] cap. 3 pagg. 59 -78; cap. 4 pagg.90-98 pagg.101-106,
cap. 5 pagg. 114-115, 119-123;
[MA1] cap. 4 pagg.136-145, pagg. 157-166, pagg.210 -214;
[BDM] cap. 4 pagg. 158-161, cap.5 pagg. 193-201, cap. 6 pagg. 241-251;
[VV] cap. 6 pag. 101-106, 122-128.
Enunciati:
1- La dimensione dell'ortogonale W di un sottospazio V di R^n di dimensione k e' n-k;
- infatti dei vettori mutamente ortogonali non nulli sono indiependenti (si moltiplica scalarmente una loro combinazione lineare per uno qualsiasi di essi e si ottine la sua norma al quadrato per il suo coefficiente nella combinazione)
- quindi si prendono una base ortogonale di V (che avra' quindi k elementi) e una base ortogonale del suo ortogonale W: essa dovra' essere base di tutto R^n e quindi avere n elementi.
2- L'immagine di una funzione lineare L da R^n in R^m e' un sottospazio vettoriale
- esso e' generato dalle colonne della matrice (mxn) associata ad L, e la sua dimensione sara' il massimo numero di colonne indipendenti.
3- La funzione lineare L e' iniettiva se e solo se L(0, ..., 0)=(0, ..., 0)= 0.
- {v in R^n : Lv = 0 } e' un sottospazio vettoriale di R^n, si dice nucleo di L , Ker L.
- e' l'ortogonale alle righe della matrice associata ad L
- ora il massimo numero di righe indipendenti e' eguale al massimo numero di colonne indipendenti
(infatti se il massimo numero di colonne indipendenti e' k vi e' una sottomatrice kxk con determinante non nullo, mentre tutte le sottomatrici quadrate di dimensione maggiore hanno detreminante nullo. Quindi anche le righe corrispondenti a questa sottomatrice sono indipendenti, e se ce ne fosse una in piu' da loro indipendent vi sarebbe una sottomatrice (k+1)x(k+1) con determinante non nullo contrariamente a quanto assunto).
4- ha quindi dim Ker L +dim Im L = dim dom L =n
5- nel caso m=n si ottiene:
una funzione lineare L da R^n in se
e' iniettiva se e solo se e' surgettiva .
6- Principio di sovrapposizione : se L e' una funzione lineare da R^n in R^m , e w in R^m
data una soluzione v del sistema nxm : L v = w
allora tutte le soluzioni sono del tipo v+x
con x soluzione del sistema omogeneo con termine noto nullo L x= 0 ,
in altre parole l'insieme delle soluzioni e' il traslato di Ker L con v (v+ Ker L).
14-11-08 esercitazione 8 (Mauro) Operare sui grafici: disequazioni ed equazioni risolte graficamente, grafici di esponenziale e logaritmo, grafici e sottografici
17-11-08 lezione 15 (Tortorelli) Dopo aver descritto le principali proprieta' delle funzioni calcolate da polinomi , viste anche come sottospazio vettoriale dello spazio vettoriale reale delle funzioni reali di variabile reale, ed illustrato genericamente il grafico di polinomi e piu' in particolare i grafici fondamentali delle funzioni di tipo esponenziale e logaritmico, si e' affrontato il problema generale seguente:
- come riconoscere in una legge data da formule l'andamento grafico della funzione ( ove aumenta ove diminuisce, il tipo di inflessione, l' area di parti di sopragrafico e sottografico etc. )
-viceversa dato un andamento grafico come scrivere una legge con esso compatibile.
Si sono quindi introdotte le nozioni di funzione monotona, convessa, lette tramite le funzioni di rapporto incrementale, ed di limite per arrivare alla definizione di derivata e alla sua interpretazione geometrica. Cenno alla differenziabilita' in due variabili e alle derivate parziali.
Riferimenti: [EB] cap. 3 pagg. 78 -89;
cap. 4 pagg.90-98 pagg.101-106;
cap. 6 pagg. 143-157;
cap. 8 pagg. 201-210, 212-215, 217-221, (anche di ricapitolazione su argomenti svolti in precedenza)
cap 9 pagg 234-243;
letture cap 5 pagg130-139, cap 6 pagg. 157-165 piuttosto interessanti.
[MA1] cap. 4 pag.130 pag, 133, pagg. 152- 156, 168-177, 185-188
pagg. 215 -219 (per le lezioni precedenti su funzoni trigonometriche)
cap. 5 pagg. 221-226;
[BDM] cap. 4 pagg. 161-164, cap. 6 pagg. 215-235, cap.7 pagg. 257-263 , 268-273,
273-275, cap. 8 pagg.297-303, 310-313, 314-319, 324-326;
[IRS] cap 2 pagg. 49-59 cap. 3 pagg.113-124;
[VV] cap. 6 pag. 106-111, 128-147, cap.7 pagg. 148-49.
Definizioni: - polinomio a coefficienti reali, grado di un polinomio, prodotto di polinomi.
-Funzione monotone:
f:A--> R si dice (monotona) crescente su A
p.o. x ,z in A se z >o= x allora f(z) >o= f(x)
f:A--> R si dice (monotona) decrescente su A
p.o. x ,z in A se z >o= x allora f(z) <o= f(x)
f:A--> R si dice (monotona) strettamente crescente su A
p.o. x ,z in A se z > x allora f(z) > f(x)
f:A--> R si dice (monotona) strettamente decrescente su A
p.o. x ,z in A se z > x allora f(z) < f(x)
OSSERVAZIONE: l'unione di grafici di funzioni crescenti non e' detto sia il grafico di una funzione crescente.
OSSERVAZIONE: se si conosce un punto del grafico di una funzione crescente allora il restante grafico deve essere nel primo e nel terzo quadrante di centro il punto dato.
- Corda con estremi sul grafico di una funzione f reale di variabile reale definita su un intervallo
e' l'immagine per t in [0;1] di t(z,f(z)) + (1-t) (b, f(b)) =(b,f(b)) + t ((z, f(z)) -(b,f(b)))
cioe' l'insieme { (t z+ (1-t)z , t f(z) +(1-t) f(b)): t in [0;1] }
cioe' il pezzo di retta y= (x-b) (f(z)-f(b))/(z-b) + f(b)=x (f(z)-f(b))/(z-b) +f(b)-b (f(z)-f(b))/(z-b).
-Il coefficiente angolare di una corda con estremi (b, f(b)) e (z,f(z)) sul grafico di f
(funzione definita su un intervallo I) si dice rapporto incrementale con centro b:
Rbf (z) = (f(z)-f(b))/ (z-b)
-Sottoinsiemi convessi:
Un sottoinsieme C di R^n si dice convesso se
per ogni coppia di suoi punti P e Q tutto il segmento con estremi questi due punti e' contenuto in C
cioe': p.o. P e Q in C e p.o. t in [0;1] si ha Q+t(P-Q) in C
funzioni convesse: una funzione reale f si dice convessa su un insieme convesso C se
il suo sopragrafico su C, {(x,y): f(x) <o= y e x in C }, e' convesso.
-Limiti:
data una funzione f definita su A ( sottoinsieme di R^m a valori in R^n ) e un punto b approssimabile con punti di A (a_n in A: distanza da a_n a b -->0 per n--> +oo)
* si dice che f tende a L per x che tende a b in A se:
per ogni soglia di errore E>0 nell'immagine
vi e' una soglia di errore D>0 nel dominio per cui se
0< dist( b, x) <o= D
allora
dist (L, f(x)) <o= E
in breve: p.o. E>0 es.D>0 t.c. p.o.x in A 0<|x-b|< D ==> |f(x) -L| < E
Si scrivera' in tale caso f(x)---> L per x -->b in A.
* Se e' a valori reali si dice che f tende a +oo per x che tende a b in A se:
per ogni soglia M nell'immagine
vi e' una soglia di errore D>0 nel dominio per cui se
0< dist( b, x) <o= D
allora
f(x) >o= M
in breve: p.o. M es.D>0 t.c. p.o.x in A 0<|x-b|< D ==> f(x) > M
Si scrivera' in tale caso f(x)---> + oo per x -->b in A.
Del tutto analoga la definizione di f(x) ---> -oo.
* Se e' di variabile reale si dice che f tende a L per x che tende a +oo in A se:
per ogni soglia di errore E>0 nell'immagine
vi e' una soglia N nel dominio per cui se
x >o= N
allora
dist (L, f(x)) <o= E
in breve: p.o. E>0 es. N t.c. p.o.x in A x>N ==> |f(x) -L| < E
Si scrivera' in tale caso f(x)---> L per x -->+oo in A.
Del tutto analoga la definizione di f(x) ---> L per x-->-oo.
* Se e' reale a variabile reale si dice che f tende a +oo per x che tende a +oo in A se:
per ogni soglia M nell'immagine
vi e' una soglia di N nel dominio per cui se
x >o= N
allora
f(x) >o= M
in breve: p.o. M es.N t.c. p.o.x in A x>N ==> f(x) > M
Si scrivera' in tale caso f(x)---> + oo per x -->+oo in A.
Del tutto analoga le definizioni con +oo, -oo.
- Se esiste il limite del rapporto incrementale (f(x) -f(b))/(x-b) per x-->b
(finito o meno)
si dice derivata prima di f in b, e si indica con f'(b) o Db f o df/dx |b o df(b)/dx
OSSERVAZIONE: non sempre tale limite esiste, in effetti non sempre vi e' tangente ad un grafico:
si pensi alla funzione f(x)= x sin 1/x per x non 0 , ed f(0)=0
essa si annulla in tutti i punti x= 1/(k pigreco) quindi i rapporti incrementali di centro 0 ed estremo in questi punti son nulli
d'altronde questa funzione in tutti i punti x =1/(2k pigreco + pigreco/2) vale x, quindi i rapporti incrementali di centro 0 ed estemo in tali punti vale 1
quindi non puo' esistere per x-->0 il limite dei rapporti incrementali
in quanto vi sono almeno due valori distinti che il rapporto incrementale di centro 0 assume comunque si sia vicini a 0.
Si noti che con un minimo sforzo si mostra che R0,f (z) puo' assumere tutti i valori tra -1 ed 1
per z in ogni intervallino bucato [-D,D]\{0}.
- La retta tangente al grafico (x,f(x)), x in I, di f nel punto (b,f(b)) nel caso in cui f'(b) sia finito,
e' la retta che e' grafico della funzione affine r(x)= f'(b) x +f(b) -f'(b)b= f'(b)(x-b) +f(b)
cioe' l'insieme (x, f'(b)(x-b) +f(b)), x in I,
cioe' y=f'(b)(x-b) +f(b) , x in I.
Nel caso infinito la tangente sara' una retta verticale (non grafico).
- Si consideri una funzione di variabile reale a valori vettori per esempio in R^2: F(x)= (f(x), g(x));
se le sue componenti sono funzioni derivabil, con derivata finita, per x=b si indica con F'(b) il vettore che ha come componenti le derivate delle funzioni componenti : (f'(b), g'(b)).
Lo si chiama vettore velocita' nel punto F(x).
Il vettore velocita' unitario tangente ad un grafico con derivata finita in un punto (b,f(b)) e' in effetti il vettore (1, f'(b))/ radice{1+ (f' (b))^2}
- Se il vettore velocita' e' non nullo (F'(b) non= (0,0)) allora la retta F(b) +t F'(b), t in R,
e' la retta tangente all'immagine di una opportuna restrizione di F ad un intervallino centrato in b.
In effetti ``si potrebbe passare'' nel punto F(b) un'altra volta con diversa direzione:

-Approssimazione lineare:
l'esistenza della derivata finita in b e' una proprieta' piu' forte della semplice esistenza geometrica della retta tangente al grafico in (b,f(b)). In effetti l'esistenza di f'(b) equivale a dire che si sbaglia poco a fare il cammino ( t, f(t)) percorrendo la retta tangente con velocita' costante (1, f'(b)) (percorrendola in modo lineare):
f(x) = f(b) + f'(b) (x-b) + r(x) con r(x)/(x-b) --->0 per x-->b
cioe' la funzione si puo' approssimare con una funzione affine ed un errore ``percentualmente infinitesimo'' (rispetto all'errore di approssimazione di b con x nel dominio).
- se f e' definita in A sottoinsieme di R^2 si dira' approssimabile linearmente o differenziabile in (a,b) se
vi sono H e K per cui
f(x,y) = f(a,b) + H (x-a) + K (y-b) + r(x,y) con r(x,y)/radice{ (x-a)^2 +(y-b)^2}-->0
per (x-a)^2 +(y-b)^2 ---> 0
La funzione affine (u,v)---> Hu +Kv +f(a,b) e' l' approssimante e l'errore e' relativamente piccolo
rispetto all'errore dist((a,b), (x,y)) che si fa sul dominio per approssimare (a,b) con (x,y).
Nel caso x-->f(x, b) ha la derivata rispetto a x in a
e y-->f(a, y) ha la derivata rispetto a y in b
e sono rispettivamente i numeri H e K. Sono le derivate parziali.
Enunciati:
- Lo spazio vettoriale dei polinomi di grado minore eguale ad n si identifica con R^n
per esempio (a,b, c) corrisponde ad a x^2+bx +c
somma di vettori corrisponde alla soma di polinomi
e prodotto per un numero corrisponde al polinomio per quel numero.
- Teorema 0: il prodotto di due polinomi ha come grado la somma dei gradi dei due fattori
- Teorema 1:
un polinomio P(x) con coefficienti non tutti nulli si annulla in a se e solo se
P(x)=(x-a) R(x) con 1+deg R=deg P
DIM.:
i) un polinomio Q(y)= b_0 + b_1 y + ... + b_m y^m e' nullo per y=0 se e solo se b_0 =0.
Nel caso Q(y) = y( b_1 + ... + b_m y^{m-1})
ii) Si scriva P mettendo in risalto (x-a):
P(x) = P(x-a +a) = Q(x-a) con deg Q= deg P
( per esempio se P(x) = 3- 2x +5x^2 e a=1 si ha
P(x)=P(x-1+1)= 3 -2(x-1+1) + 5(x-1+1)^2= 1 -2(x-1) + 5(x-1)^2 +5 + 10(x-1)=
= 6 +8(x-1) + 5(x-1)^2 = Q(x-1) con Q(y)= 6+8y +5y^2 e y=x-1)
iii) Se P si annulla per x= a allora Q si annulla per y =x-a=0, ma allora Q(y)=y S(y) e
quindi P(x)= (x-a)S(x-a).
- Teorema 2: un polinomio con coefficienti reali non tutti nulli ha un numero di radici minore o eguale al suo grado.
DIM.: se a_1 ... a_k sono radici del polinomio P allora P(x)= (x-a_1) ... (x-a_k) R(x) quindi deve avere almeno grado k. Quindi k <o= deg P.
-Teorema 3 (Principio di identita' dei polinomi) Se due polinomi danno gli stessi valori in un numero di punti maggiore dei loro gradi allora hanno gli stessi coefficienti (sono lo stesso polinomio).
DIM.: Se P e Q sono due polinomi il grado di P(x)- Q(x) e' al piu' il maggiore del grado dei due,
quindi dovrebbe avere al piu' un tal numero di radici se non avesse coefficienti tutti nulli.
Diversamente avrebbe coefficienti tutti nulli e quindi P e Q avrebbero eguali coefficienti.
-Teorema 4 (Divisione: solo enunciato): Dato un polinomio P di grado maggiore o eguale di un polinomio D
vi sono unici due polinomi Q ed R con deg R < deg D per cui
P= DQ+R
-Teorema 5( Decomposizione di polinomi: solo enunciato) Ogni polinomio a coefficienti reali si puo' scrivere come una costante moltiplicata per un prodotto di potenze di fattori del tipo (x-a) e di fattori del tipo ((x-b)^2 +c^2) essendo quest'ultimi i fattori corrsipondenti a trinomi di secondo grado con discrimiante negativo.
-Teorema 6 (comportamento all'infinito) : se deg P > deg Q , e c >0 allora vi e' M per cui se
|x|> M allora |P(x)|> c |Q(x)|.
DIM.: nel caso piu' semplice P(x)= a x^n , Q(x)=b x^m con n>m.
In effetti se |x| > radice n-m di{ c|b|/|a|} si ottiene quanto richiesto.
Nel caso generale si prende il termine leader di P, diciamo a x^n, e si trovano via via n +m +1 soglie in modo che | a x^n| sia maggiore di n+m+1 il maggiore tra i moduli di tutti gli altri addendi di P e di c Q. Si avra' per la diseguaglianza triangolare |P| > |ax^n| -| termini restanti di P|
ma per la scelta fatta si ha anche
|ax^n|> (n+m+1) )(il massimo in modulo tra i vari addendi del resto di P e di cQ)>
> somma dei moduli dei termini restanti di P e di quelli di cQ>
> | termini restanti di P| + c|Q|.
- conoscendo le radici, il grado di un polinomio, e il segno del coefficiente di grado massimo,
si puo' approssimativamente tracciare un andamento del grafico corrispondente.
- cautela va usata nel tracciar grafici di polinomi e va tenuto presente il grado per evidenziare intersezioni tra grafici di polinomi per valori della x grandi o fuori scala.
-Grafico di e^x e di e^{-x} e delle loro inverse rispettiv log x e -log x
Grafici di a^x = e ^{a logx}
-Le funzioni trigonometriche non possono essere calcolate da polinomi perche' hanno immagini limitate da -1 ed 1 mentre i polinomi hanno immagini rette o semirette;
per altro i grafici delle funzioni trigonometriche intersecano le rette orizzontali o in infiniti punti o in nessun punto, mentre i grafici di polinomi intersecano tali rette in un numero finito di punti.
La funzione e^x non puo' essere calcolata da polinomi:
in effetti si era detto che la successione del tasso di interesse composto
(1+x/n )^n e' crescente per n > -x e il suo limite per n -->+oo e' proprio e^x
ma allora per x >0 e^x> (1+x/n)^n per ogni n cioe' di un polinomio di grado n grande a piacer
nostro
quindi preso un polinomio qualsiasi P(x) se n > deg P vi sara' una soglia M per cui se x >M
(1+x/n)^n > P(x) . In particolare per tale P e^x > P(x) per x >M.
- Una funzione f e' crescente su un intervallo I se e solo se
per ogni a in I la funzione x---> Raf(x) e' non negativa
-Una funzione f e' convessa su un convesso C se e solo se
p.o. t in [0;1] f( tz +(1-t)b)) <o= tf(z) + (1-t) f(b)
ora tz +(1-t)b e' il generico punto dell'intervallo, nel dominio di f, di estremi b e z
mentre tf(z) + (1-t) f(b) e' il punto ad esso proporzionale che sta nell'intervallo, nell'immagine di f,
di estermi f(b) e f(z)
questo vuol dire che il grafico della funzione tra i punti (b,f(b)) e (z,f(z))
sta sotto la corda con gli stessi estremi (ovvero tale corda sta nel sopragrafico)
(tale corda e' il grafico della funzione affine g:x--> (x-b) Rbf(z) + f(b), x tra b e z,
questa funzione e' quella che trasforma il generico punto nell'intervallo di estremi b e z in quello che ha la sua stessa proporzionalita' con gli estremi f(b) ed f(z) nell'intervallo dell'immagine
g(tz +(1-t)b) = tg(z) + (1-t) g(b)= tf(z) + (1-t) f(b)).
Quindi se la funzione e' convessa visto che il sopragrafico contiene il grafico questa condizione e' soddisfatta. Viceversa se tale condizione e' soddisfatta a maggior ragione la funzione e' convessa
(il segmento con estermi punti del sopragrafico sta sopra il segmento che ha come estremi le proiezioni in verticale di quei punti sul grafico).
************************OSSERVAZIONE (non fatta a lezione)*******************
Si osserva che se una funzione e' convessa e quindi il suo grafico sta sopra la corda di estremi (b,f(b)) e (z,f(z)) se si considera x fuori dall'intervallo di estremi b e z, diciamo dalla parte di z,
poiche' (z,f(z)) deve stare sotto la corda di estremi (b,f(b)) e (x, f(x)) il punto (x,f(x)) deve stare sopra la retta passante per (b,f(b)) e (z, f(z)). Con ragionamento analogo sincerarsi del viceversa.
In parole piane si e' provato:
una funzione e' convessa se e solo se
il suo grafico sta sopra i complementari delle corde con estremi su di esso.
***************************************************************************
- Se quindi si conoscono solo due punti del grafico di una funzione convessa si puo' dire
solo che essa sta sotto la corda tra i due punti e sopra il complementare della stessa.
- Solo enunciato con argomentazione pittorica:
una funzione f e' convessa su un intervallo I se e solo se
per ogni b in I la funzione z--->Rbf(z), z in I\{b}, e' crescente.
Un argomento geometrico e' comunque semplice, due casi :
. se il centro b del rapporto incrementale non e' in mezzo agli altri due punti
x, z essendo quest'ultimo il piu' lontano da b, si ottiene che (x,f(x)) deve stare sotto la corda
di estremi (b, f(b)) e (z,f(z)): quindi Rbf(x) < o= Rbf(z)
.. se piuttosto il centro e' ``al centro'' e poniamo che z venga prima di b ed x, il punto (z, f(z)) deve stare sopra la retta passante per (x,f(x)) e (b,f(b)) ma ... allora la velocita' uniforme per recarsi da f(z) a f(b) debbe esser maggiorata da quella invariata per condursi da f(x) allo stesso f(b).
Viceversa immediatamente da tale proprieta' di monotonia si deduce quella della corda, piu' sopra provata esser equivalente alla convessita'.
- Una funzione f ha derivata finita in a se e solo se
vale l'approssimazione lineare al primo ordine
[f(x) - f(b) - f'(b) (x-b)] / (x-b) --->0 per x-->b
si usa la propritea' dei limiti per cui una quantita' tende ad un limite finito se essa meno questo valore tende a zero.
20-11-08 lezione 16 (Tortorelli) Dopo aver introdotto la nozione di intorno, e dimostrato la ovvia proprieta' di monotonia del passaggio al limite, si sono delineati tre capitoli per lo studio di funzioni:
-1 derivate in relazione a monotonia e convessita', teoremi di Lagrange e Cauchy, sino ad arrivare a valori di massimo e minimo e punti di massimo o minimo relativi;
-2 problemi di esistenza dei valori di massimo e minimo e studio della surgettivita':
estremo superiore o inferiore, funzioni continue, teoremi del valor intermedio, di Weietsrass,
e sull'inversa di funzioni continue su intervalli (tutti di un pezzo!);
-3 studio dell'andamento dei grafici agli estremi del dominio o in punti di esso interessanti nei casi particolari in esame: andamento lineare all'infinito, asintoti obliqui, ordine di annullamento,
notazione di Landau O e o, metodo per lo studio di rapporti di somme di infiniti o infinitesimi.
Riferimenti:
[EB] cap. 8 pagg. 221-223, cap 8 pag 239, cap 9 pagg 265-281, 286-287;
[MA1] cap. 5 pagg. 226-228, 248-259;
[BDM] cap. 4 pagg. 161-164, cap.7 pagg. 273-275, 275-281, cap. 8 pagg.319-321;
[IRS] cap 2.6 pag 73, cap 2.7.2 pag. 78, cap. 2.7.3-2.7.4 pagg 83-84, cap. 3 pagg.113-124;
[VV] cap.7 pagg. 153-159.
Definizioni notazioni: -Un insieme U e' intorno di p in R^n se contiene una palla centrata in p,
cioe' esiste r>0 per cui se dist(p,q) < r allora q e' in U
e.g. per n=2 con p=(a,b) deve esistere r per cui se (x-a)^2+ (y-b)^2 <r^2 allora (x,y) in U
per n= 1 deve esistere r per cui se -r < x-p <r allora x in U
un insieme U e' intorno di +oo (-oo) in R se esiste C per cui U contiene la semiretta [C,+oo)
( (-oo, C])
cioe' se x > o = C allora x in U.
- Se U e' intorno di p allora U\{p} si dice intorno bucato di p
(espressione non usata a lezione ma qui introdotta per comodita')
- Funzione concava su un convesso.
- Punti interni ad un intervallo.
- Funzione derivata e derivate successive con relative notazioni.
- Un sottoinsieme A di R^n si dice limitato se e' contenuto in qualche palla
cioe' esiste r>0 per cui se p e' in A allora la sua distanza dall'origine || p|| < r
e.g. per n=2 deve esistere r per cui se (x,y) e' in A allora (x-a)^2+ (y-b)^2 <r^2
per n= 1 deve esistere r per cui se x e' in A allora -r < x<r
un insieme A e' limitato superiormente (inferiormente) in R se esiste C per cui A e' contenuto nella semiretta (-oo, C] (risp. [C,+oo))
cioe' se x e' in A allora x <C.
- Una funzione f si dice limitata su B se lo e' la sua immagine su B cioe':
se esiste r per cui per ogni x in B si ha ||f(x)||< r
- Una funzione f si dice limitata superiormente (inferiormente) su B
se lo e' la sua immagine su B.
- M si dice massimo ( minimo) di un sottoinsieme A di R se:
1- M in A
2- p.o x in A si ha M >o= x ( M <o= x)
cioe' il piu' grande (piccolo) tra gli elementi di A
- M si dice valore massimo ( valore minimo) di una funzione f su B se lo e' per l'immagine di f su B, cioe':
1- esiste x in B per cui M = f (x) [M dev'essere un valore di f su B]
2- p.o x in B si ha M >o= f(x) ( M <o= f(x))
cioe' il piu' grande (piccolo) tra i valori assunti elementi da f su B.
- Notazioni: max A, min A, max_B f , min_B f
- Un punto p del dominio della funzione f si dice punto di massimo relativo (minimo relativo)
se vi e' un intorno di p per cui f(p) = max_{U intersezione dom f} f;
e.g. in R p e' punto di massimo relativo se
esiste r>0 per cui f(x) <o= f(p) se p -r< x< p+r
*****************************ATTENZIONE ********************************
a lezione e' stata probabimente detta, invece di quanto appena scritto, una inesattezza cioe':
se p e' punto di massimo relativo
allora
vi e' r f e' crescente su (p-r, p] ed f e' decrescente su [p, p+r)
questo non e' vero (il viceversa e' vero ed e' quanto si usa generalmente nella pratica!)
si pensi come controesempio al grafico di -( 1+ x^2(1+sin 1/x)) per x non 0 e -1 per x=0
funzione minor eguale di -1
con infinite oscillazioni vicino a 0 quindi mai crescente ne decrescente a destra o a sinistra di 0
``compresso'' tra i grafici -y= 1+ 2x^2 (parabola) e y=-1 (retta orizzontale)
In effetti essendo derivabile ovunque con derivata cos1/x -2x(1+sin 1/x) per x non 0 e derivata nulla in 0
si osserva che per x>0 nei punti x_n = 1/( pig 2n) tale derivata vale 1-1/pig n >0
nei punti z_n =1/(pig (2n+1)) vale -1- 1/pig n<0
quindi per i teoremi esposti nella presente non puo' essere ne crescente ne decrescente il
alcun intervallo (0, E), poiche' comunque si fissi E>0 si trova un n in N per cui 0< x_n, z_n <E.
*************************************************************************
Essendoci insiemi, funzioni limitati senza massimo e minimo si considerano le nozioni seguenti
- L si dice estremo superiore ( inferiore ) di un sottoinsieme A di R se:
1- esiste una successione x_n in A x_n ---> L per n--->+oo
[puo' non esser un elemento di A ma deve essere approssimabile con elementi di A]
2- p.o x in A si ha L >o= x ( L <o= x )
[comunque dev'esser piu'grande di tutti gli elementi di A]
- L si dice estremo superiore ( inferiore) di una funzione f su B se lo e' per l'immagine di f su B, cioe':
1- esiste una successione x_n in B f( x_n) ---> L per n--->+oo M
[puo' non essere un valore di f su B ma dev'essere approssimabile con valori di f su B]
2- p.o x in B si ha L >o= f(x) ( L <o= f(x))
[comunque dev'esser piu'grande di tutti i valori di f su B]
- Notazioni: sup A, inf A, sup_B f , inf_B f
- Se p in B sottoinsieme di dom f , la funzione f si dice continua in p su B se
f(x)---> f(p) per x-->p e x in B
-Una funzione si dice continua su B se e' continua in ogni punto di B su B.
-Notazione di Landau o e O:
f e' O(g) intorno a p se esiste un numero M ed un intorno U di p per cui valga
|f(x)| <o= M |g(x)| per x in U\{p}
f e' o(g) intorno a p se esiste un intorno U di p e una funzione definita su U per cui
h(x) --> 0 per x-->p
|f(x)| <o= h(x) |g(x)| per x in U\{p}
Se g non e' nulla nell'intorno di p tranne al piu' il punto p le due nozioni sono equivalenti
rispettivamente a
|f|/|g| e' limitata in un intorno di p
|f|/|g| ---> 0 per x--->p
Enunciati:*
PRIMO CAPITOLO
Monotonia del passaggio al limite:
se i valori di due funzioni sono sempre nello stesso ordine in un intorno bucato allora la stesso ordine rimane per gli eventuali valori limite
se
F --> A , G--> B per x-->p ed F(x) >o= G(x) in un intorno bucato di p
allora A >o= B
DIM.: per mostrare A >o= B basta mostrare A-B >o= 0 e quindi basta mostrare che
per ogni E >0 si ha A-B >o= -E
Poiche' A-B= A-F(x) + F(x)-G(x) -(B-G(x))
siccome dato E >0, per ipotesi di convergenza, vi e' un intorno U bucato ove vale
-E < A-F(x), B-G(x) < E
si ottiene per x in U\{p}
A-B >o= -2E + F(x)-G(x)
d'altra parte, per l'ipotesi F >o= G, vi e' un intorno V bucato ove F-G >o=0
quindi A-B >o= -2E .
Teorema 1. Se f e' cerscente su un intervallo I , esiste f '(p) p in I allora f ' (p) >o= 0.
DIM.:
si usa la monotonia del limite con F(x)=(f(x)-f(p))/(x-p) >o= 0 poiche' f e' crescente e G=0.
Osservazione: - Potrebbe essere f strettamente crescente ma f ' (p)=0
e.g. f(x)=x^3 poiche' x^3-z^3 =(x-z)(x^2 +xz+z^2) e il secondo fattore ha uno dei due discriminanti negativo per x non z
f e' strettamente crescente. Inoltre ( x^3-0^3)/(x-0) =x^2 ---> 0 per x-->0, quindi f '(0)=0.
- Vi sono funzioni f per cui f '(p) >0 (diseguaglianza stretta) ma in nessun intorno di p la funzione e' monotona crescente
e.g. si tracci un grafico di una qualsiasi funzione f per x>0 in modo che
i- sia compreso tra quelli y= x^2+x e y=x (quindi f(0)=0)
ii- oscilli infinite volte, toccandoli, tra i due grafici, in un intorno di 0,
iii- in modo che la corda tra i due punti di contatto con l'uno e con l'altro abbia pendenza negativa (almeno per i contatti di ascisssa abbastanza vicina a 0).
Per iii- il grafico disegnato non puo' quindi essere crescente in nessun intorno di 0.
Inoltre poiche' x+1= (x^2+x - (0^2 +0))/(x-0) >o= f(x)/x >o= x-0/x-0 =1 esiste f ' (0)=1>0.
***************************ATTENZIONE******************************
L'espressione analitica data a lezione ( x^2/2(1+sin 1/x +2/x)) per esemplficare quanto sopra,
e' in realta' crescente e quindi non verifica iii-.
Si e' mostrato questo come esercizio sulle derivate nella lezione successiva.
*********************************************************************
Volendo un'espressione analitica di una funzione con questo tipo di grafico si puo' considerare
f(x) = x^2/2 ( 1+sin 4/(x) + 2/x) per x>0 ed f(0)=0
*************************************************************************
Cio' si puo' verificare anche senza uso dei teoremi sulle derivate enunciati appena di seguito:
in effetti poiche' il seno e' minore eguale di 1 e maggiore eguale di -1 la funzione e' minore eguale di x^2 +x e maggiore eguale di x
Quindi x+1>o= f(x)/x >o= 1 per cui esiste f ' (0)=1.
Inoltre quando il seno e' eguale ad 1 la funzione e' eguale a x^2 +x
mentre quando il seno e eguale a -1 la funzione e' eguale a x.
Ma ogni x per cui il seno e' eguale a -1 e' del tipo 4/(3pig/2 +2pig n) n in N
e l'ascissa appena precedente per cui il seno e' eguale a 1 e' 4/(pig/2 +2pig (n+1)).
Il segno della pendenza della corda tra i punti del grafico corrispondenti e' quello di
segno [1/(3pig/2 +pig 2n) - 1/(pig/2 +pig 2(n+1)) (1+4/(pig/2 +pig 2(n+1) ) ]=
segno [ (pig/2 +pig 2(n+1))^2 - (4+ pig/2 +pig 2(n+1))(3pig/2 +pig 2n)] =
segno[ (pig/2 +pig 2(n+1))^2 - (4+ pig/2 +pig 2(n+1))(pig/2 +pig 2(n+1) - pig)] =
segno[ -4 (pig/2 +pig 2(n+1))+ 4 pig +pig (pig/2 +pig 2(n+1) )] =
segno[ (-4 + pig )(pig/2 +pig 2(n+1))+ 4 pig ] < 0 per ogni n in N essendo 4 - pig>17/20.
Certo con le derivate si semplificherebbe molto. Provare per esercizio.
**************************************************************************
Teorema 2 (di Lagrange) Se f e' derivabile in (a;b) ed f-->f(a) per x-->a, f-->f(b) per x-->b
allora vi e' c : a< c < b e (f(b)- f(a))/(b-a) = f ' (c)
Piuttosto che dimostrare tale teorema lo si esemplifica a livello intuitivo.
Si considera un fatto geometrico intuitivo: per una curva che sia
i- piana
ii- con tangente in ogni suo punto
iii- fatta ``tutta di un pezzo'' (o meglio ``tutta percorribile con un solo cammino'')
ogni corda con estremi sulla curva ha una tangente alla curva ad essa parallela. Si pensi di traslare parallelamente a se stessa la retta determinata dalla corda in direzione di un pezzo limitato di curva staccato dalla corda: quando la retta lascia questo pezzo di curva si ha tangenza.
Le tre ipotesi sono necessarie. Se non c'e' la prima ipotesi si pensi alla corda che congiunge i due estremi del profilo di una scala a chiocciola cha bbia fatto un giro, e' verticale
mentre la scala a chiocciola non lo e' mai. Se non c'e' la seconda si pensi ad un angolo ha solo due tangenti e una corda trasversale non e' ad esse parallela. Per la terza ipotesi si pensi ad un angolo senza il vertice, oppure ad un segmento ed ad un punto (qui non c'e' tangente univocamente determinata) non allineato con questo.
(aperta parentesi
Se l'immagine della funzione t--->(g(t),f(t)) e' un cammino (in cui non si ha mai velocita' nulla) che descrive la curva a cui si sta pensando si deve avere che il vettore determinato dalla corda per due punti(g(b), f(b)) - (g(a), f(a)) dev'essere linearmente dipendente da qualche vettore tangente che sara' del tipo (g ' (c), f '(c)) cioe' si deve annullare il determinante
(g(b) -g(a)) f ' (c) - (f(b) -f(a)) g '(c)
Il teorema di Lagrange rientra in questo schema intuitivo pensando come curva il grafico
(t, f(t)).
Teorema di Cauchy: Se f e g soddisfano le stesse ipotesi del teorema di Lagrange
e g(a) e' diverso da g(b) allora per qualche punto intermedio c diverso da a e b si ha:
(f(b) -f(a))/(g(b)-g(a)) = f '(c)/ g ' (c)
Un enunciato che partcolarizza il teorema di Lagrange e' piuttosto il seguente
Teorema di Rolle: nelle solite ipotesi se f(a)=f(b) allora vi e' c intermedio e diverso da a e b per cui f '(c)=0
Usualmente si dimostra il caso particolare (Rolle) usando la continuita' e il teorema di Weierstrass, quindi Lagrange e quindi Cauchy.
chiusa parentesi)
Teorema 2 bis: Se f e' derivabile su un intervallo I ed f ' >o=0 allora f e' crescente su I.
DIM.: Infatti ogni rapporto incrementale essendo un valore di derivata sarebbe non negativo.
L'ipotesi che tutto debba avvenire su un intervallo ( in quanto insieme fatto ``tutto di un pezzo'') e' basilare. Come al solito una funzione che in (0;1) vale 1 e in (1;2) vale 0 ha derivata nulla, quindi non negativa, ma non e' crescente, anzi nel caso e' decrescente.
Usando il teorema di Lagrange e la monotonia dei rapporti incrementali come equivalente della convessita' si prova
Teorema 3 f e' convessa e derivabile su un intervallo se e solo se
f ' e' crescente se e solo se
il grafico di f sta sopra ogni sua tangente cioe'
per ogni x e p nell'intervallo f(x) >o= f ' (p) (x-p) + f(p)
Teorema 4 Se p e' un punto di massimo o minimo relativo di f interno ad un intervallo
I ove f e' definita allora se esiste f ' (p) deve essere f '(p)=0
DIM.: per qualche s>0 (p-s; p+s) e' contenuto in I
per un 0<r <s f(p) > o = f(x) cioe' f(p)- f(x) >o= 0, per tutti gli x in (p-r; p+r)
ma allora per questi x
(f(p) - f(x))/(p-x) >o= 0 se x <p e (f(p) - f(x))/(p-x) <o= 0 se x >p
per monotonia del passaggio al limite f ' (c) e' sia minore eguale che maggiore eguale a 0. Quindi e' nulla.
Se il punto di massimo relativo non e' interno la derivata puo' benissimo essere positiva: f(x)=x su [0;1].
Teorema 4 bis I punti di massimo e minimo relativo di una funzione sono da cercarsi:
1- agli estremi degli intervalli
2- nei punti ove la funzione non ha derivata
3- nei punti ove la derivata e' nulla
Chiaramente ci possono essere punti ove la derivata e' nula che non sono ne di massimo ne di minimo relativo per esempoi per f(x)=x^3, -1<x < 1, e p=0.
Teorema 4 ter Sia f definita su un intervallo
f e' ivi costante se e solo se esiste f ' ed e' sempre nulla
DIM.: se f e' costante i rapporti incrementali sono nulli quindi convergono a 0.
Viceversa dato p nell'intervallo poiche' la derivata e' finita si ha
[f(x) - f(b) - f'(p) (x-p)] / (x-p) --->0 per x-->p e in particolare f(x)---> f(p) per x --> p
quindi si uo' applicare il teorema di Lagrange er due qualsiasi punti a e b dell'intervallo
ottenendo f(b) -f(a) = (b-a) f ' (c) =(b-a) 0 =0.
Teorema 5
f e' convessa e due volte derivabile su un intervallo I se e solo esiste f '' non negativa su I
DIM.: Si usa il teorema 3 e quindi i teoremi 1 e 2bis per f ' invece che per f.
SECONDO CAPITOLO
Dopo avere esposto i fatti principali per lo studio delle ``gobbe e dei su e giu' '' di un grafico
vanno affrontati i problemi relativi alla surgettivita' delle funzioni, a com'e' fatta la loro immagine piu' in generale.
Un fatto rilevante da ossrvare e' che insiemi e funzioni limitati non e' detto che abbiano massimo o abbiano minimo. Si pensi a f(n) = 1/n , n in N i valori di tale funzioni sono maggiori di 0
ma 0 non e' un suo valore, pur avicinandosi i suoi valori arbitrariamente ad esso.
Similmente artan x < pig/2 e artan x = pig /2 non ha soluzioni
purtuttavia per x sempre piu' grande artan x si avvicina sempre piu' a pig /2.
I concetti per trattare queste occorrenze sono quelle di estremo superiore ed estremo inferiore.
Teorema 6 Il fatto che ogni insieme limitato non vuoto abbia estremo superiore ed inferiore e' equivalente alla completezza per successioni e alla proprieta' di Archimede.
Teorema 6 bis
L' estremo superiore di f su B e' il piu' piccolo tra i numeri piu' grandi di tutti i valori di f su B
cioe' sup_B f = min { y : y >o= f(x) , per ogni x in B}
Un valore di massimo (minimo) e' estremo superiore (inferiore).
Chiaramente non sempre e' vero il viceversa (per questo si e' introdotto il concetto).
Quando esistono massimo e minimo di una funzione?
Quando si puo' ridurre lo studio della surgettivita' alla ricerca di estremo superiore ed inferiore?
Per rispondere a tali domande niente di meglio che le funzioni continue.
Vista la definizone va detto che grosso modo una funzione e' continua su ``un insieme tutto di un pezzo'' quando il suo grafico su tale insieme e' anch'esso ``tutto di un pezzo''.
COME COSTRUIRE FUNZIONI CONTINUE
- (x,y) --> x+y e' continua DIM. |x+y -(a+b)| <o= | x-a| +|y-b|
- (x,y) --> xy e' continua DIM> | xy-ab|=|xy-xb +xb-ab| <o= |x||y-b| + |x-a||b|
- le funzioni derivabili con derivata finita sono continue
DIM. nel caso vale l'approssimazione lineare
[f(x) - f(b) - f'(p) (x-p)] / (x-p) --->0 per x-->p e in particolare f(x)---> f(p) per x --> p.
- le funzioni convesse sono continue nei punti interni (si tralascia la dimostrazione).
-COMPOSIZIONE DI FUNZIONI CONTINUE E' CONTINUA.
- se n funzioni f_1 ... f_n sono continue sullo stesso dominio la funzione vettoriale
(f_1, ..., f_n ) e' continua.
-teorema 9 qui sotto.
Teorema 7 (degli zeri o del valore intemedio: surgettivita')
Se f e' continua su [a,b] e assume valori di segno opposto agli estremi
allora in un punto intermedio si annulla.
Cio' e' equivalente ad affermare che
Una funzione continua f su un intervallo I
ha immagine su I che e' a sua volta un intervallo che contiene ( inf_I f ; sup_I f).
(in altri termini una funzione continua su un intervallo assume tutti i valori compresi tra il suo estremo superiore e il suo estremo inferiore.)
Osservazioni:
Si osserva che se assume anche massimo e minimo allora si ha Im_I f =[inf_I f, sup_I f].
La condizione che la funzione si definita su un intervallo e' necessaria in quanto un intervallo e' ``tutto di un pezzo''.
Il teorema dice quindi che
le funzioni continue trasformano insiemi tutti di un pezzo in insiemi tutti di un pezzo.
Ora i sottoinsiemi di R tutti di un pezzo sono giusto giusto gli intervalli. Ma in altri ambiti gli insiemi tutti di un pezzo sono piu' complicati, le funzioni continue no e continuano a trasformare insiemi tutti di un pezzo in inisemi tutti di un pezzo.
Teorema 8 (Weierstrass: massimi minimi)
Una funzione continua definita su un intervallo chiuso (con gli estremi) e limitato
(estremi finiti) [a, b] cioe' un segmento con estremi
(ma basta un'unione finita di segmenti chiusi)
e' limitata su [a,b] anzi assume valore massimo e valore minimo su [a,b].
Osservazioni:
qui il punto non e' che il dominio sia un'unione finita di intervalli ma che questi siano limitati e
con gli estremi : la proprieta' del domino necessaria che si puo' dedurre dalle ipotesi perche' una funzione continua su di esso assuma massimo e minimo e' che ogni successione di elementi del dominio abbia una restrizione che converga a qualche elemento dl dominio.
Ebben se ci si pensa un attimo si capisce che un enunciato piu' astratto del teorema e' il seguente:
le funzioni continue trasformano un insieme in cui ogni successione di suoi elementi abbia una restrizione che converge a qualche elemento dell'insieme stesso in un insieme con la stessa proprieta'.
Se togliamo l'ipotesi di continuita' della funzione il teorema e' falso si pensi alla funzione 1/x
per x in (0,1] e nulla per x=0, quindi definita su tutto [0,1] ma non continua in 0. Non e' limitata.
Se il dominio non fosse chiuso lo stesso esempio mostra che il teorema non sussisterebbe: 1/x e' illimitata ma continua su (0,1].
Se poi il dominio non e' limitato la funzione (x^2-1)/x^2+1) ovvero artan x su R sarebbero altri semplici controesempi.
Mettendo insieme i due ultimi teoremi con un po di fantasia si ottiene
Corollario se f e' continua su un intervallo (a, b) anche non limitato e
inf f < A, B< sup f
f--> A per x--> a f---> B per x--> b
allora
f assume massimo e minimo su (a,b) e
im_(a,b) f = [ min_(a,b) f , max_(a,b) f ]
Teorema 9 Ogni funzione strettamente monotona e' iniettiva.
Se f e' continua su un intervallo I ed e' iniettiva in I allora
1- e' strettamente monotona in I
2- la sua inversa e' continua sull'intervallo im_I f
Osservazioni:
da quanto detto le funzioni radici sono tutte continue, e avendo dimostrato la continuita' delle funzioni trigonometriche le inverse delle loro restrizioni sarebbero tutte continue, cosi come il logaritmo avendo la continuita' dell'esponenziale.
Che il dominio sia tutto di un pezzo e' necessario: si pensi alla funzione eguale ad x in [0,1)
e a -x+2 su (1,2): continua iniettiva ma non monotona sul dominio , quindi anche prendendo la funzione eguale ad x su [0,1) e eguale a x-2 su [3,4] si avrebbe addirttura una funzione continua strettamente crescente con imaggine l'intervallo [0,2] ma con inversa non continua in 1. Se poi la funzione non e' continua si modifica il primo esemppi in un punto e si considera la funzione definita su [0,2) eguale ad x fino ad 1 e per valori maggiori di 1 eguale a -x+2.
Per ottenere in altri ambiti piu' generali questo teorema la proprieta' rilevante del domino garantita dall'ipotesi non e' semplicemente che sia tutto di un pezzo ma che il grafico ``non si avvolga su se stesso'': il tempo quotidiano misurato dalla lancetta delle ore di un orologio da' una bella funzione iniettiva dalla circonferenza al segmento [0,12) che e' iniettiva ma non continua nella posizione mezzogiorno/mezzanotte, pur essendo l'inversa continua.
In termini piu' concisi la funzione t-->(cos t , sint) e' continua iniettiva su [0,2 pig ) ma la sua inversa non e' continua: se mi avvicino al punto (1,0) con ordinata positiva ottengo 0, con ordinata negativa 2 pig .
TERZO CAPITOLO
Si tratta dello studio del grafico agli estremi del domino o in punti dello stesso interessanti nei casi particolari che possono essere in esame.
Per esemplificare la problematica piu' semplice ci si puo' chiedere se il grafico di f in un introrno di infinito puo' stare sotto una retta y=ax+b,
per qulache a e b f(x) < o= ax +b intorno a +oo.
O se il grafico di una funzione che ha valore minimo 0 assunto in un punto p nell'intorno di p sta sotto ogni parabola y= a(x-p)^2 ( con a>0) nell'intorno di p,
per ogni a>0 f(x)< a(x-p)^2 nell'intorno di p.
Questo tipo di problema si risolve in molti casi con il calcolo di un limite.
Nel primo esempio la risposta e' positiva se
f(x)/x --> L<+oo per x-->+oo in particolare risulta f e' O (x) in +oo
nel secondo se
f(x)/(x-p)^2 -->0 per x-->p ovvero f e' o( (x-p)^2) in p
Si osservi che nel primo caso non e' detto sia presente alcun asintoto obliquo:
e.g. il grafico di f(x) = x + log x non puo' avere asintoti obliqui a +oo (f(x) -x-->+oo) pur stando sotto tutte le rette y=mx (m>1) intorno a +oo poiche' f/x --> 1 per x-->+oo.
In generale si tratta di ``confrontare asintoticamente'' una funzione con certe altre note, e per questo e' sufficiente calcolare (se esistono) i limiti dei rapporti e vedere se sono finiti o nulli o meno.
Funzioni tipiche di confronto sia all'infinito che in p=0 sono
e^x, e^{ax^s}, |x|^s , |log x|^q, loro prodotti.
Va osservato che la notazione di Landau deve scriversi specificando nell'intorno di quale punto si stanno confrontando le grandezze:
e.g. x e' o(x^2 ) in +oo
ma x^2 e' o(x) in 0.
Va menzionata la funzione f(x)= e^{-1/x^2} se x non 0 e f(0)=0 essa ha la particolarita'
f(x)/x^n --->0 per x-->0 qualsiasi sia l'esponente n della funzione potenza con cui si fa il confronto.
Un metodo (gia' testato su semplici successioni) per studiare limiti del tipo rapporto di somme di infiniti (o somme di infinitesimi) e' stabilire sia nel numeratore che nel denominatore se vi e' un addendo di cui i rimenenti sono o, quindi raccoglierlo a fattor comune e ridurre lo studio del limite del rapporto a quello del rapporto di queste due grandezze dominanti.
se A_2 e' o(A_1), A_3 e' o(A_1), B_1 e' o(B_3), B_2 e' o(B_3), B_2 e' o(B_3)
nell'intorno dello stesso punto p
si ottiene:
R= (A_1+A_2+A_3)/(B_1+B_2 +B_3+B_4) =
A_1/B_3 (1+A_2/A_1 +A_3/A_1)/(1+B_1/B_3 +B_2/B_3+B_4/B_3) =
A_1/B_3 (1+o(1))/(1+ o(1))
quindi R ha lo stesso comportamento asintotico in p di A_1/B_3
.
21-11-08 esercitazione 9 (Mauro) Campi di esistenza, limiti notevoli e derivate delle funzioni elementari, studi di funzioni (cfr. appunti delle esercitazioni).
21-11-08 lezione 17 recupero (Tortorelli) Precisazioni e correzioni alla precedente lezione.
Regole di calcolo dei limiti in particolare: criterio di nonesistenza ed unicita' del limite, principio e teorema di sostituzione, principio di confronto il criterio dei ``due carabinieri'' .
Limiti notevoli: confronto di infiniti ed infinitesimi, continuita' delle funzioni elementari con dimostrazione, limiti dei principali rapporti incrementali .
Alcune anticipazioni sulle regole di derivazione, e loro dimostrazioni,
per lo studio della monotonia di di x^2/2(1+ sin 1/x +2/x)
In particolare derivata della funzione composta e della funzione inversa e del prodotto cenno di dimostrazione.
Esercizio lasciato studiare la derivabilita' di arsin 2x/(1+x^2).
Riferimenti: [EB] cap 10 pagg. 313-320,
[MA1] cap. 4 rilettura della parte che riguarda i limiti;
[BDM] cap.7 pagg. 263-278;
Enunciati:*
REGOLE PER I LIMITI
0- Monotonia del passaggio al limite (cfr. precedente lezione)
1- principio di confronto e criterio dei carbinieri (due carabinieri certe volte ne basta uno)
se c--> a e C-->a , x-->p e c <o= B <o= C nell'intorno bucato di p
allora
B--> a , x-->p
Chiaramente se a e' infinito basta un solo carabiniere:
se a =+oo basta considerare la sola diseguaglianza c <o= B per ottenere la tesi,
se a= - oo basta considerare la sola diseguaglianza B<o= C.
A parole:
se una funzione e' compresa tra due funzioni che hanno lo stesso limite nell'intorno bucato del punto limite allora esiste il limite di questa funzione nello stsso punto
1-bis
f-->a in R^n se e solo se dist(f,a)= |f-a|-->0
1-ter [IMORTANTE NON DETTO A LEZIONE]
se f e' crescente (decrescente ) in I= (a,p) allora si ha f --> sup_I f, x-->p (inf_I f)
2- limiti di somme
se f-->a e g--b per x --> p allora f+g--> a+b
se a e b non sono entrambi infiniti con segno diverso
2-bis
se f--> oo , x-->p e g e' limitata intorno a p allora f+g--> oo
3- limiti di prodotti
se f-->a e g-->b per x --> p allora fg--> ab
se a e b non sono uno infinito e l'altro nullo
(intesi: +oo(-oo)=-oo, +oo c=+oo se c>0, +ooc=-oo se c<0, -oo c=-oo se c>0, -ooc=+oo se c<0)
3-bis
se f-->0 , x-->p e g e' limitata intorno a p allora fg--> 0
3-ter se g-->b in R , x-->p in allora g e' limitata nell'intorno di p
4- limite del reciproco
se f-->a , x--> p se a in R\{0} allora 1/ f--> 1/a
se f-->0 , x--> p se f e' di segno costante intorno a p allora 1/f --> (sign f )oo
se |f|--> +oo , x--> p allora 1/f --> 0
5- unicita' del limite e criterio di non esistenza del limite
se f--> L e f-->M , x-->p allora L=M
se vi sono due successioni nel dominio di f per cui
x_n -->p, n-->+oo in N e f(x_n)--> L allora f non ha limite per x-->p
z_n -->p, n-->+oo in N e f(z_n)-->M e M diverso da L
6- principio di sostituzione
se l'immagine di g nell'intorno bucato di p e' contenuta nel dominio di f, e
se f(y)--> L, y-->q e y= g(x)-->q , x-->p allora f(g(x))--->L , x-->p
provveduto che almeno una delle seguenti due condizioni sia verificata:
f--> f(q) , y-->q ovvero g sia diversa da q nell'intorno bucato di p
7- se f_1 --> a_1 , ..., f_n --> a_n (con limiti finiti) per x-->p allora (f_1, ... f_n)---> (a_1, ... a_n)
DIM.(alcune): 1- nel caso a finito: si consideri E>0
in un intorno bucato U di p c(x)-a <o= B(x) -a <o= C(x)-a
esiste un intorno bucato V di p per cui -E< c(x)-a < E
esiste un intorno bucato W di p per cui -E< C(x)-a < E
quindi nell'intorno bucato intersezione dei tre si ha -E < B(x)-a< E.
1 ter - Dato E>0
per definizione esiste x_n tale che
f(x_n)--> sup f, n-->+oo, in particolare
esiste m per cui se n>m-1 allora f(x_n) > sup f -E (per sup f=+oo allora f(x_n)>E)
si ponga D=p-x_m ( per p =+oo porre D=x_m) allora
se p-x <D, cioe' x>x_m , per monotonia f(x) >o= f(x_m) > sup f - E (per sup f=+oo f(x) > E).
3- si prova prima 3-ter: dato E=1 vi e' un intorno bucato di p in cui b-1 < f(x)<b+1.
quindi si prova 3-bis: 0<o= |f(x)g(x)|=|f(x)||g(x)| < |f(x)|M quindi carabinieri.
quindi nel caso a e b finiti 0<o= |f(x)g(x)-ab|=|f(x)g(x)-ag(x) + ag(x)-ab| <o=
|f(x)g(x)-ag(x)|+|ag(x)-ab|=|f(x)-a||g(x)|+|a||g(x)-b|, ancora carabinieri.
quindi nel caso a=+oo, b>0 finito: dato E=b/2 vi e' un intorno bucato di p |g(x)-b| <b/2
in particolare in tale intorno g(x)> b/2, per cui ivi |f(x)||g(x)| > |f(x)|b/2, carabiniere.
7- (dist((f_1, ...f_n),(a_1 ...a_n))^2 = (f_1(x) - a_1)^2 + ... +(f_n(x) - a_n)^2 --> 0 per x-->p.
Osservazioni:
Piu' che dimostrare 6 conviene capire perche' sono necessarie le ipotesi, e ancora di piu' la sua importanza pratica.
Consideriamo:
f=1 per y diverso da q=2 e f(2)=3 ;
g= 4 per x diverso da p=5 e da 5+1/n e g(5+1/n)=2=q
f(g(x))= 1 per x diverso da 5+1/n mentre f(g(5+1/n))=3. Quindi f(g(x)) non ha limite in p.
La valenza pratica e' che per quanto sia complicata g la sitratta come una scatola chiusa come una variabile. La difficolta' sta nel riconoscere g nelle varie formule, isolando i termini giusti che la identificano, ed eventualmente aggiungendo/togliendo o moltiplicando/dividendo per opportuni termini per metterla in risalto se ce ne fossero solo alcuni pezzi.
Con il principio di sostituzione quello di confronto, cio' l'uso di diseguaglianze per sondare l'esistenza e in molti casi calcolare limiti, e' il principale strumento elementare per lo studio dei limiti.
LIMITI NOTEVOLI
- Limiti di continuita' e di alcune funzioni di base, gli altri si deducono da questi:
se f e' costante eguale a c nell'intorno bucato di p allora f-->c , x-->p
x--> p per x-->p
(1+x/n)^n --> e^x, n-->+oo inoltre per gli n >o= -x e' una successione crescente.
e^x --> e ^p , x-->p in R, (dimostrato a lezione: vedi sotto)
sin x --> sin p, x-->p in R, (dimostrato a lezione: vedi sotto)
cos x --> cos p, x-->p in R, (cos x= sin (x+pig/2 ))
radice n-sima {n} -->1, n-->+oo (non enunciato a lezione)
-Limiti infiniti ed infinitesimi i principali:
x--> p per x-->p quindi i polinomi all'infinito vanno all'infinito
x^a-->+oo , x-->+oo se a >0 (se a>o= 1 per x>1 si ha x^a >o= x: caramba; se a<1 per x> M^{1/a}si ha x^a > M: definizione di limite)
x^a--> +oo , x--> 0, x>0 se a <0 (reciproco del precedente)
b^x -->+oo , x-->+oo, se b>1 (dimostrato a lezione per b=e vedi sotto)
b^x --> 0 , x-->+oo, se b<1 (reciporoco del precedente)
log x --> +oo, x-->+oo ( per monotonia di log x se x > e ^M allora log x > M quindi per definizione di limite segue quanto voluto)
log x --> -oo , x-->0, x >0 ( come sopra x<e^{-M})
b^x/x^a --> + oo, x -->+oo, se b>1 e a >0
|x|^a b^x --> 0 , x--> - oo, se b>1 e a >0 (y=-x e' il reciproco del precedente)
per sostituzione e passando al reciporco nel primo caso, facendo la potenza 1/a nel secondo si ottengono:
|log_b y |^a / y -->0 , y--> +oo, se b>1 e a >0
|log_b y| |y|^{1/a}-->0, y-->0 , se b>1 e a >0
x^x/ b^x-->+oo, x--> +oo (si passa ad esponenti in base e, l'eponente e' xlog x/b che per x>eb e' maggiore di x: caramba)
n!/b^n --> +oo , n-->+oo , se b>1 (n!=n(n-1)... 2, n!/b^n = n/b (n-1)/b... 2/b 1/b sia m il piu' grande intero piu' piccolo di b
n!/b^n > n (m/b...2/b (1/b)^2): caramba)
n!/n^n --> 0 , n-->+oo (n!/n^n = n/n (n-1)/n ... 1/n < 1/n: caramba)
b^n/n^a --> +oo, n -->+oo, se b>1 e a>0 (restrizione ad N di b^x/x^a)
- Principio del confronto per il rapporto di somme di infiniti o del rapporto di somme di infinitesimi(cfr. lezione precedente)
-Limiti dei principali rapporti incrementali
sinx/x --> 1 , x-->0
(1-cosx)/x^2 -->1/2, x-->0
(e^x-1)/x -->1 , x-->0 e per sostituzione log(1+y)/y -->1 , y-->0.
DIM.: dimostrazioni, che gia' non compaiono nell'enunciato, di alcuni dei risultati sopra elencati
e^x --> e ^p , x-->p in R e' equivalente a e^x - e^p --> 0, ma e^x-e^p =e^p(e^{x-p} -1) posto x-p=y
per n>-y (1=y/n)^n e' crescente, si ha:
per n > - y e^y > (1+y/n)^n, sostituendo - y a y nella stessa diseguaglianza e passando ai reciproci
per n > y 1/(1-y/n)^n > e^y
quindi
per n > |y| 1/(1-y/n)^n - 1> e^y - 1 > (1+y/n)^n - 1
poiche' A^n-B^n=(A-B)(A^{n-1} + A^{n-2}B + ...+ B^{n-1})
per n>|y| y/(n-y) (n addendi ognuno -->1 per y-->0) > e^y -1 > y/n (n addendi ognuno -->1 per y-->0)
Quindi si conclude con i carabinieri.
sin x --> sin p, x-->p in R,
sinx - sin p=
sin ((x+p)/2+(x-p)/2) - sin (x+p)/2-(x-p)/2 = sin((x+p)/2)cos((x-p)/2) +sin((x-p)/2)cos((x+p)/2) - sin((x+p)/2)cos((x-p)/2) + sin((x-p)/2)cos((x+p)/2) =
= 2 sin((x-p)/2)cos((x+p)/2)
per cui |sinx - sin p | <o= 2|sin ( (x-p)/2)|
ma |sin t|<o = |t| (il segmento che congiunge una corda e' minore della lunghezza della corda) per cui |sinx - sin p | <o= |x-p|.
b^x -->+oo , x-->+oo, se b>1 b^x= e^{xlog b} , y=xlog b >0, e^y > (1+y/n)^n> 1+y.
b^x/x^a --> + oo, x -->+oo, se b>1 e a >0
sia m>a, m in N : per x>1 x^a < x^m
b^x= e^{xlogb} > ( 1+ xlog b/(m+1))^{m+1} poiche' xlog b>0
quindi
b^x/^a > ( polinomio in x di grado m+1)/x^m = x (logb/(m+1) + o(1))-->+oo per x -->+oo.
radice n-sima {n} -->1, n-->+oo radice n-sima {n} = e^{1/n log n} 1/nlog n e' restrizione di y= 1/x log x -->0 per x-->+oo
per continuita' e^y--> e^0 =1
sinx/x --> 1 , x-->0 poiche' x e sin sono funzioni dispari sinx/x=|sin x|/|x|
|sinx|/|x| <o= 1 ( la corda ae' piu' lunga del segmento che congiunge i suoi estremi)
per |x|< pig/2 |tan x|/|x| >o= 1 (il settore sotteso dall'arco del cerchio unitario di lunghezza |x| ha area |x|/2 minore dell'area
del triangolo di base il raggio unitario e di altezza tan x che ha area |tan x|/2)
quindi |cos x | <o= sin x/x <o= 1 carabinieri.
(1-cosx)/x^2 -->1/2, x-->0 (1-cosx)/x^2= (1-(cosx)^2)/x^2 1/(1+cos x) = (sin x/x)^2 1/(1+cos x) -->1 /2 per x-->0
poiche' per |x|<1 cos x=+rad{1-(sin x)^2} -->1 per x-->0 essendo la radice continua in quanto inversa di una continua.
(e^x-1)/x -->1 , x-->0 come sopra osservato per n > |x|
x/(n-x) (n addendi ognuno -->1 per x-->0) > e^x -1 > x/n (n addendi ognuno -->1 per x_->0)
si ottiene dividendo per x>0, rispettivamente per x<0,
1/(n-x) (n addendi ognuno -->1 per x-->0) > ( e^x -1)/x > 1/n (n addendi ognuno -->1 per x_->0)
1/(n-x) (n addendi ognuno -->1 per x-->0) < ( e^x -1)/x < 1/n (n addendi ognuno -->1 per x_->0)
si conclude con i carabinieri.
log(1+y)/y -->1 , y-->0. log(1+y)=g(y)=x , g(y)=0 solo per y=0, f(x) = x/(e^x-1) log(1+y)/y =f(g(y)): sostituzione.
E ora un classico della sostituzione
se f--> a , g-->+oo e f/g-->0 per x-->p allora (1+ f/g)^g --> e^a per x-->p se a in R
--> +oo se a=+oo
--> 0 se a=-oo
(1+f/g)^g = e^{g log (1+f/g)} = e^{ f g/f log(1+f/g)} =e^{ f 1/(f/g) log (1+f/g)};
per sostituzione, essendo per i limiti notevoli F(y)= 1/y log(1+y), F(0)=1 continua,
y=f/g, si ha 1/(f/g) log (1+f/g)-->1;
quindi z=g log(1+f/g)--> a, ancora per sostituzione dai limiti notevoli infiniti o dalla continuita'
di e^z si ottiene il limite.
un altro modo di vedere la cosa (1+fh)^{1/h} con f-->a, h-->0 e fh-->0, o anche
F^g con g(1-F)-->a, g-->+oo, F-->1.
24-11-08 lezione 18 (Tortorelli) Correzione di un enunciato delle precedenti lezioni e studio della monotonia intorno a zero di
x^2(1+sin 1/x)(cfr. lez.16).
Ripetizione delle regole di derivazione e calcolo delle derivate delle funzioni di base.
Regole di de l'Ho^pital.
Sviluppo di Taylor e sua unicita'.
Calcolo dei polinomi di Taylor di esponenziale seno coseno e log(1+x) con centro 0.
Esempio di calcolo del polinomio di Taylor usando sviluppi noti ed unicita'.
Convergenza degli sviluppi di Taylor per esponenziale seno coseno, e per log(1+x) se |x|<1.
Il polinomio di Taylor di centro 0 di f(x)= e^{-1/x^2} per x non 0 e f(0)=0 e' il polinomio nullo.
Riferimenti:
[EB] cap. 9 pagg. 244-251, cap.10 pagg. 320-324 (sviluppi in serie), ;
[MA1] cap. 5 pagg. 226-242 (l'approccio e' un po diverso da quello dato a lezione),
243-248 (de L'Ho^pital), pagg.259-269 (Taylor) ;
[BDM] cap. 8 pagg.302-312, 313-314, 319-323;
[IRS] cap 2 pagg. 58-76;
[VV] cap.7 pagg. 150-152, 159-169.
Definizioni: polinomio di Taylor di grado (minore eguale a) n e di centro p: P(y)= f(p) +f'(p) y +... 1/k! f^(k)(p) y^k +... + 1/n! f^(n) (p) y^n.
Resto di Lagrange di ordine n e centro p: 1/(n+1)! f^(n+1) ( z) (x-p)^(n+1) con z strattamente compreso trea z e p.
Enunciati e dimostrazioni: TABELLA DERIVATE :
la derivata di sin x e' cos x.
la derivata di e^x e' e^x.
DIM.: sin x-sin p=
sin ((x+p)/2+(x-p)/2) - sin (x+p)/2-(x-p)/2 = sin((x+p)/2)cos((x-p)/2) +sin((x-p)/2)cos((x+p)/2) - sin((x+p)/2)cos((x-p)/2) + sin((x-p)/2)cos((x+p)/2) =
= 2 sin((x-p)/2)cos((x+p)/2)
(sinx - sin p)/(x-p) = sin ((x-p)/2) / ((x-p)/2) cos((x+p)/2) ---> 1 cos p=cos p per , x-->p (limite notevole sint/t -->1, t-->0, e continuita' coseno)
(e^x - e^p)/(x-p) = e^p ( e^{x-p} -1)/(x-p) --->1 , x-->p ( x-p= t e limite notevole (e^t-1)/t -->1, t-->0)
REGOLE DI DERIVAZIONE
- se f e g sono derivabili in un punto con derivata finita e r in R allora f+rg e' derivabile nel punto con derivata finita e (f+rg)' = f' + r g'
in altre parole
le funzioni derivabili in un punto e con derivata finita sono uno spazio vettoriale e la derivata e' una trasformazione lineare da questo spazio su R.
le funzioni derivabili in ogni punto di uno stesso intervallo e con derivata finita sono uno spazio vettoriale e la derivata e' una trasformazione lineare da questo spazio allo spazio vettoriale di tutte le funzioni sull'intervallo dato (trasformazione non surgettiva! gli interessati chiedano)
(se poi una o entrambe le derivate in un punto di f e di rg sono infinite, nel caso con infiniti dello stesso segno, la formula e' ancora valida).
- se f e g sono derivabili con derivata finita allora fg e' derivabile con derivata finita nel punto e (fg)' = f'g + f g'
(se poi una o entrambe le derivate in un punto di f e di g sono infinite, e nel punto almeno una delle due funzioni sia continua e diversa da 0, la formula e' ancora valida a patto che gli infiniti che vi compaiono siano dello stesso segno).
- se f e' derivabile e continua in punto allora 1/f e' derivabile nel punto e (1/f)' = - f'/f^2
- se f e g sono derivabili in un punto con derivata finita allora f/g e' derivabile nel punto con derivata finita e (f/g) '= (f'g -fg')/g^2
- sia g una funzione con immagine di un intorno di un punto q contenuta nel domino di una funzione f:
se f e' derivabile con derivata finita in g(p) e g e' derivabile con derivata finita in p allora x-->f(g(x)) e' derivabile in p e (f(g(p))' =f'(g(p)) g'(p)
(se poi f ' (g(p)) e' non nulla g '(p) puo' essere infinta e la formula e' ancora valida;
se piuttosto f '(g(p)) e' infinita con f continua in g(p) con
g derivabile in tutto un intorno di p e con derivata continua in p e nonnulla la formula e' ancora valida)
regola della catena y=g(x) d(f(g))/dx = df/dy dy/dx
- se f e' una funzione invertibile e continua in un intorno di p quindi monotona strettamente
se f e' derivabile in p allora f^{-1} (la funzione inversa) e' derivabile in q=f(p) e (f^{-1})' (f(p)) = 1/f'(p) cioe' (f^{-1})' (q)= 1/f' (f^{-1} (q))
(se f'(p)=0 l'uguaglianza si intendera' con -oo se f e' decrescente, con +oo se f e' crescente, se f'(p)=oo l'uguglianza e' con 0)
y=f(x) dy/dx = dx/dy
In effetti se si considera che il grafico dell'inversa e' simmetrico rispetto alla bisettrice del grafico della funzione , poiche' la retta ad esso
tangente sara' la simmetrica della tangente al grafcio della funzione nel punto simmetrico, tali rette dovranno avere coefficenti angolari
che siano uno il reciproco dell'altro.
DIM.: (svolta a lezione il prodotto nel caso finito, ed accennato alla dimostrazione regola della catena, e alla formula per la derivata dell'inversa).
Dalle derivate precedenti e dalle regole di derivazione si ottengono le derivate di x^p, tan x, artan x, arsin x, arcos x.
Regole di de l'Ho^pital.
Siano f e g derivabili con derivata finita in (a,p) allora se
-g ' e' non nulla
- f--> 0 e g--> 0 per x-->p
oppure f--> oo e g--> oo per x-->p (non importa il segno)
- f' /g' --> L per x--> p
allora anche g e' non nulla (Lagrange-Rolle) e f/g--> L per x--> p.
Teorema (sviluppo di Taylor): Sia f una funzione derivabile n-1 volte su un intervallo I, sia p in I, e vi sia la derivata n-sima di f in p finita.
Allora esiste un unico polinomio P(y) di grado minore eguale a n per cui
(f(x)- P(x - p))/(x-p)^n -->0 x-->p
Tale polinomio e' f(p) + f'(p)y + 1/2f''(p) y^2 +... + 1/k! f^(k) (p) y^k +...+ 1/n! f^(n)(p) y^n . In altri termini
f(x)= P(x-p) + o ((x-p)^n) = f(p) + f'(p)(x-p) + 1/2f''(p) (x-p)^2 + .... + 1/n! f^(n)(p) (x-p)^n + o((x-p)^n) , x--->p
Se poi in tutto I vi e' la derivata (n+1)-esima continua allora per ogni x in I si puo' esprimere tale resto in maniera piu' determinata
esiste uno z compreso strettamente tra p ed x per cui
f(x) = f(p) + f'(p)(x-p) + 1/2f''(p) (x-p)^2 + .... + 1/n! f^(n)(p) (x-p)^n + 1/(n+1)! f^(n+1) ( z) (x-p)^(n+1)
La funzione derivata di una funzione pari e' una funzione dispari, mentre la derivata di una funzione dispari
e' una funzione pari.
Per una funzione dispari: le derivate di ordine pari saranno dispari, quelle di ordine dispari saranno pari.
Per una funzione pari : le derivate di ordine pari saranno pari, quelle diordine dispari saranno dispari.
Inoltre una funzione dispari continua in 0 si deve annullare in 0.
Quindi nello sviluppo di Taylor centro 0 di una funzione pari compaiono solo derivate di ordine pari, che sono pari, essendo quelle
di ordine dispari dispari e quindi tutte nulle in 0.
Nello sviluppo di una funzione dispari centro 0 compariranno similmente solo le derivate ordine dispari, che sono pari, essendo quelle
di ordine pari dispari e quindi tutte nulle in 0.
Per funzioni pari lo sviluppo di ordine 2m coincidendo con quello di ordine 2m+1 ha un resto (di Lagrange) di ordine infinitesimo O(x^{2m+2}) piuttosto che solo O(x^{2m+1})
Similmente per funzioni dispari lo sviluppo di ordine 2m+1 coincidendo con quello di ordine 2m+2 ha un resto (di Lagrange) di ordine O(x^2m+3) piuttosto ch esolo di ordine O(x^{2m+2}).
sin x =
x - x^3/6 + x^5/120 + .... + (-1)^m x^{2m+1}/(2m+1)! (-1)^{m+1}cos z x^{2m+3}/(2m+3)!
cos x =
1 - x^2/2 + x^4/24 -x^6/720 + ... + (-1)^m x^{2m}/(2m)! + (-1)^{m+1} sin z x^{2m+2}/(2m+2)!
Per l'esponenziale
e^x =
1+ x +x^2/2+x^3/6+x^4/24+x^5/120+x^6/720 + ..... x^n/n! + e^z x^{n+1}/(n+1)!
Sia per le funzioni trigonometriche qui sopra che per l'esponenziale i resti dei polinomi di Taylor di diverso ordine n, a x fissato,
come successione in n tendono a 0 per n-->+oo
InfattI seno e coseno di z=z(n,x) sono limitati, per e^{z(n,x)} si osserva che e' minore di 1 se x<0 o di e^x se x>0. Quindi si usa il aftto che x^M/M! -->0.
Si potra' scrivere per ogni x in R per queste funzioni
e^x = 1+ x +x^2/2+x^3/6+x^4/24+x^5/120+x^6/720 + .....
sin x = x - x^3/6 + x^5/120 + ....
cos x =1 - x^2/2 + x^4/24 -x^6/720 + ...
Non sempre si puo' fare!
Per log(1+x)= x - x^2/2 + x^3/3 -x^4/4 + ... + (-1)^{n-1} x^n/n! +(-i)^n/(n+1) x^{n+1}/(1+z)^{n+1}
per |x|<1 il resto e' infinitesimo, ma per x>1non si puo' dire.
si osserva che la sua derivata ha come sviluppo, sviluppo i cui termini sono proprio le derivate dello sviluppo di log(x+1), la serie geometrica con ragione -x di cui e' limite per |x|<1
1/(1+x) = 1 - x + x^2 -x^3 + ... + (-1)^{n-1} x^{n-1} +(-1)^n x^n/(1+x)
che in effetti per x>1 non converge.
Consideriamo f(x) = e^{-1/x^2} se x non nullo e f(0)=0
si ha f(x) = o (x^n) per ogni n in N basta ricondursi ai limiti notevoli con la sostituzione y=1/x^2.
ma allora f coincide con il suo resto di Taylor centro l'origine per ogni ordine: i suoi polinomi di Taylor sono tutti nulli.
O meglio si potrebbe dedurre cio' se si sapesse che f e' derivabile quante volte si vuole in 0.
In effetti cio' e' vero , quindi la f ha polinomi di Taylor.
Sicuramente tale f non e' eguale alla serie dei sui polinomi di Taylor che son tutti nulli pur essendo f non identicamente nulla.
25-11-08 esercitazione 10 recupero (Mauro) studi di funzione.
27-11-08 lezione 19 (Tortorelli)
- Si sono presentate le principali nozioni teoriche per l'integrazione alla Riemann, anche per funzioni di piu' variabili, basata sull'idea intuitiva di misurare le aree, dei sottografici di funzioni
non negative, per ``esaustione'' con somme di aree di rettangoli.
- Quindi si e' estesa la nozione a funzioni non limitate su domini non limitati, e si e' mostrato come per funzioni continue su opportuni domini si possa, mediante integrali iterati, ridursi al calcolo di integrali di funzioni di una variabile.
- Per l'integrazione in una variabile, dopo avere mostrato che se una funzione derivata e' integrabile su un intervallo allora si puo' calcolare il suo integrale come differenza agli estremi della funzione di cui e' derivata , si e' introdotta la nozione di primitiva di una funzione. Con il teorema fondamentale del calcolo integrale si e' individuata nelle funzioni continue un'ampia classe di funzioni integrabili che sono anche derivate: derivate della loro funzione integrale.
-Infine si sono passati in rassegna i metodi di integrazione basati sul teorema fondamentale.
AVVERTENZA:
la nozione di funzione sommabile (data a lezione per estendere l'integrale a funzioni non necessariamente limitate su domini non limitati) non coincide (se non nel caso di funzioni di segno costante) con la nozione di funzione integrabile in senso imporprio, o integrabile nel senso di Cauchy, data in molti testi:
tipico esempio f(x)=sin x/x sulla semiretta [1, +oo).
Riferimenti: oltre agli appunti allegati nel seguito:
[EB] cap. 9 pagg. 251-265, 281-286, 289-291, cap 10 pagg 301-313;
[MA1] cap. 6 tutto;
[BDM] cap. 9 pagg. 345-380;
[IRS] cap 2 pag 85-112;
[VV] cap.8 pagg. 170-190.
I principali enunciati e le definizioni sono riportati nelle prime quattro facciate del materiale
messo a disposizione.
APPUNTI SU INTEGRAZIONE
1-12-08 lezione 20 (Tortorelli) Ripetizione della precedente lezione e si sono introdotti i numeri complessi.
APPUNTI SU NUMERI COMPLESSI
Riferimenti: Oltre a quelli della precdente lezione sull'integrazione per i numeri complessi cfr.:
[EB] cap.15 pagg.547-554;
[BDM] cap.1 pagg.40-42, pag. 54;
[IRS] cap 5.6 pagg.180-182.
1) Visto che tra i numeri reali l'equazione x^2=-1 non ha soluzioni la si aggiunge
e la si chiama i: i^2= -1
Per i numeri complessi si sono introdotte le nozioni:
- somma e prodotto di numeri complessi
(quelle dei polinomi con la regola cha al posto di i^2 si mette -1)
- inverso z^{-1}di un numero complesso z non nullo, e relativo calcolo
- coniugato ``z sopralineato'' di un numero complesso z
- modulo |z| di un numero complesso z
Quindi si sono messe in rilievo le prime proprieta' geometriche dei numeri complessi
identificandoli con le coppie di numeri reali (a,b) = a +i b
la somma corrisponde alla traslazione
il coniugato corrisponde al riflesso rispetto all'asse ``reale'' delle ascisse
(a+ib)(x- i y)= prodotto scalare tra (a,b) e (x,y) - i det ((a,b)(x,y))
il prodotto per un numero reale non negativo alla dilatazione centro l'origine con quel fattore
Il fatto notevole e' che aggiungendo ai numeri reali le radici di z^2=-1, cioe' i e -i, si recuperano tutte le radici di ogni polinomio: e' il teorema fondamentale dell'algebra
ogni polinomio a coefficienti complessi di grado n ha esattamente n radici complesse contate con molteplicita'
ovvero se P(z)= a_0 +a_1 z + ... +a_n z^n, con a_n non 0 , e i coefficienti complessi
allora P(z) = a_n prodotti di (z-c)^k
ove la somma dei k e' n, e c sono i numeri complessi per cui P(c)=0.
2) Per gli integrali si sono sottolineati ancora i seguenti fatti e forniti altri esempi.
- gli integrali sono per funzioni non negative aree (volumi) di sottografici,
quindi sono limite di somme di aree (volumi) di rettangoli (parallelepipedi)
(base per altezza),
in particolare per una funzione continua su Q chiuso e limitato risulta integrabile e il suo integrale su Q e' limite di somme del tipo
somme f(x_i) misura (T_i) (base =misura T_i, altezza = f(x_i))
ove T_1 .... T_k e' un partizione di Q in pezzi con parte interna disgiunta
e x_i e' un qualsiasi punto di T_i
il limite si fa facendo tendere a 0 il massimo tra i diametri dei T_1, ..., T_k
- vale la proprieta' della media integrale per funzioni continue su un n-rettangolo chiuso e limitato
- la nozione di integrale si estende a funzioni non limitate su domini non limitati partendo da funzioni non negative
- l'integrale di una somma e' la somma degli integrali, l'integrale sull'unione di domini disgiunti e' la somma degli integrali
- gli integrali in piu' variabili di funzioni continue su domini opportuni, si riducono a somme di iterazioni di integrali in una variabile:
l'integrale su {(x,y): y^2 < x < -y +2, -1< y< 3} di f(x,y)= 1/(1+x^2+y^2) e' eguale a
integrale sull'intevallo (-1,2) rispetto a y di
G(y) = (integrale sull'intervallo (y^2, -y+2) rispetto a x di
g_y(x) = 1/(1+x^2+y^2) )
E' una formulazione del principio di Cavalieri.
-Teorema fondamentale del calcolo integrale:
1- se una f = F ' su [a,b] ed e' integrabile su [a,b] allora il suo integrale e' eguale a F(b)-F(a)
2- se f e' continua (e quindi integrabile su [a,b]) allora e' la derivata della sua funzione integrale
3- se F e' un'altra primitiva di f su [a,b] allora F(b)-F(a)= integrale di f su [a,b]
- Una primitiva di 1/x e' F(x)= log x +a per x>0, e F(x)=log (-x) +b per x<0 con a non necessariamente eguale a b.
- Nozione e notazione per gli integrali orientati
- Dalla regola della derivata di una funzione composta segue la regola di integrazione per sostituzione
esempi:
I= integrale tra 0 e 1 di radice di 1-x^2 in dx ,
si pone x=sin t e visto che x varia tra 0 e 1 basta far variare t tra 0 pig/2
dx =cos t dt , radice di 1-x^2 = | cos t| , 0< t< pig /2
quindi sostituendo
I= integrale tra 0 e pig/2 di cos^2 t dt
con osservazione geometrica e' eguale all'integrale tra 0 e pig/2 di sin^2 t , ma la loro somma e' eguale
all'integrale di 1 su (0 , pig/2) che e' pig/2. Quindi:
I=pig/4.
J= integrale tra 1/2 e 2 di x/ (1+x^2)^3 in dx
si pone x^2=t quindi 1/4< t< 4, dt =2x dx si sostituisce e si ha
J=1/2 integrale su (1/4, 4) di 1/(1+t)^3 dt
poiche' 1/(1+t)^3 ha primitiva -1 /2(1+t)^2 per il teorema fondamentale
J=-1/4 1/(1+16)^2 +1/4 1/(1+1/16)^2
- Dalla regola della derivata di un prodotto di funzioni si ottine la regola di integrazione per parti.
esempi:
I=integrale di (cos x )^2 visto come integrale di cos x cos x non vien bene per parti
F ' = cos x G= cos x
quindi F =sin x G' =-sin x
I= int tra 0 e y di F ' G = differenza agli estremi di FG - int F G '=
= sin ycos y - int tra 0 e y di sin x(-sin x)= sin y cos y + int sin x sin x
se ancora si pone
F' = sin x e G = sin x e quindi F=-cos x G ' = cos x si ottiene un'identita' non utile
I = siny cos y + (-cos y) sin y - int tra 0 e y di (-cos x) cos x.
Piuttosto volendo calcolare
I =integrale tra 0 e y di e^{2x} sin 3x
si osserva che si sa calcolare la primitiva di entrambi i fattori, e che
integrando due volte per parti la derivata del seno torna ad essere meno seno
e quindi portando al primo membro gli integrali si ottiene un'espressione significativa
si pone F '=e^{2x} G= sin 3x quindi F=1/2 e^{2x} G ' = 3 cos 3x
I = 1/2 e^{2y} sin 3y - int 1/2 e^{2x}3 cos 3x= 1/2 e^{2y} sin 3y - 3/2 int e^{2x} cos 3x
ponendo F '=e^{2x} G= cos 3x quindi F=1/2 e^{2x} G ' = - 3 sin 3x
(se si facesse il viceversa si otterrebbe quello di partenza e sarebbe senza utilita')
I = 1/2 e^{2y} sin 3y - 3/2 1/2 e^{2y} cos 3y +3/2 1/2 - 3/2(- int 1/2 e^{2x}(-3 sin 3x))=
= 1/2 e^{2y} sin 3y - 3/4 e^{2y} cos 3y + 3/4 - 9/4 int e^{2x} sin 3x
e quindi portando al prmo membro l'ultimo addendo
13/4 I = 1/2 e^{2y} sin 3y - 3/4 e^{2y} cos 3y + 3/4
2-12-08 esercitazione 11 recupero (Mauro) Esercizi su integrazione.
4-12-08 lezione 21 (Tortorelli) Calcolo delle radici complesse di trinomi di secondo grado; fattorizzazione in campo complesso di polinomi a coefficienti reali, calcolo delle radici quarte di -1 in forma cartesiana.
Impostazione del calcolo della primitiva di 1/(t^4+1).
Forme trigonometrica ed esponenziale di un numero complesso:
argomento principale, calcolo delle radici ennesime di un numero complesso, calcolo in forma trigonometrica delle radici quarte di -1.
Convergenza della serie esponenziale all'esponenziale complessa e relazioni con le funzioni trigonometriche.
Tassi di variazione (velocita') in funzione delle grandezze dipendenti e indipendenti (posizione e tempo).
L'equazione differenziale y '(x) = y(x), metodo del fattore integrante per trovare tutte le soluzioni di: y'(x) = c y(x), y'(x)= f(x) y(x).
APPUNTI SU NUMERI COMPLESSI
Riferimenti:
[EB] cap.15 pagg. 554-560, cap. 11 pagg. 334-346;
[MA1] cap.8 pagg.337-340, 343-347;
[BDM] cap.6 pagg.252-253, cap. 8 pagg. 329-331;
[IRS] cap 5.6 pagg.182-185, cap. 6 pag. 221-222, pagg. 228-229;
[VV] cap.9 pagg. 191-197.
Definizioni e notazioni: parte reale e parte immaginaria di un numero complesso z:
Im z e Re z , z = Re z+ i Im z; il campo dei numeri complessi C;
forma trigonometrica o polare di un numero complesso z=x+i y:
z= r ( cos t + i sin t ), r =|z| (cioe' r^2 = x^2 +y^2 e r>0 ), t in R.
argomento principale di un numero complesso z:
e' l'unico t tra 0 e 2pig per cui z=|z| (cos t + i sin t);
esponenziale di un numero complesso z=x+i y: e^z = e^x (cos y + i sin y ), quindi per definizione e^{iy}= cos y + i sin y ;
equazioni differenziali del primo ordine in forma normale e lineari omogenee
Enunciati:
- Si hanno le seguenti identita' :
|zw|=|z||w|, coniugato di (z+w) = coniug. z + coniug. w, coniugato (zw)= coniug. z coniug.w
in particolare z e' reale se e solo se e' eguale al suo coniugato.
Quindi se Q(z) e' un polinomio a coefficienti reali Q(z)= a_0 + a_1 z+... +a_n z^n
e a+i b e' una sua radice non reale ( b non 0) si ha:
a_0 + a_1(a+ib) + ... + a_n (a +ib)^n = Q(a+ib)= 0 =
= coniugato di 0 = coniugato di Q(a+ib)=
= coniug. a_0 + coniug. a_1 coniug. (a+ib) + ...+ coniug. a_n (coniug. (a+ib))^n =
= coniug. a_0 + coniug. a_1 (a-ib) + ... + coniug. a_n (a-ib)^n =
essendo i coefficienti reali
= a_0 + a_1(a-ib) + ... + a_n (a-ib)^n = Q(a-ib)
Ovvero un polinomio a coefficienti reali se ha una radice non reale ha anche la sua coniugata come radice.
Per il teorema fondamentale dell'algebra un polinomio a coefficienti reali di grado n
Q(z)= a_0 + a_1 z+... +a_n z^n, a_n non 0
e' prodotto di a_n con fattori del tipo
(z- r)^h in corrispondenza delle radici reali r,
e fattori del tipo
((z-a)^2 +b^2)^h in corrsipondenza delle due radici complesse coniugate a +ib e a-ib, b non 0
La somma delle molteplicita' delle singole radici, cioe' la somma degli esponenti k con i doppi degli altri 2h , sara' eguale ad n.
-
Arg (zw) =Arg z + Arg w +2k pig, per qualche k in Z.
Le radici n-sime di un numero complesso w sono i vertici di un n-agono regolare di raggio eguale alla radice n-esima di |w|, e primo vertice con argomento principale eguale a
(Arg w)/ n. Quindi degli angoli che identificano le radici n-sime di w sono:
(Arg w)/n, (Arg w)/n + 2pig /n , .... , (Arg w)/n + 2(n-1)pig /n
se poi (Arg w)/n < 2pig /n, sono propiro gli argomenti principali delle radici in questione.
-Si ha (1+(x+i y)/n)^n --> e ^x e^{iy} per n --->+oo
anche 1+ (x+iy) + (x+iy)^2/2 + .... + (x+iy)^n/ n! ---> e ^x e^{iy} per n --->+oo
Si verifica per x = 0
1 + i y + (iy)^2/2 + (iy)^3/6 + (iy)^4 /24 + ... + (iy)^n/n! =
1 + i y - y^2/2 - i y^3/6 + y^4 /24 + .... (iy)^n/n!
considerando i fattori con i si ha lo sviluppo di sin y che converge a sin y
considerando i fattori senza i si ha lo sviluppo di cos y che converge a cos y
per cui essendo per definizione e^{i y} = cos y +i sin y
1 + i y + (iy)^2/2 + (iy)^3/6 + (iy)^4 /24 + ... + (iy)^n/n!--->e^{iy} per n --->+oo
- Si consideri l'equazione differenziale
y '(x) = f(x) y(x) con f funzione continua su I intervallo
si cercano le tutte le funzioni con derivata definite su I per cui per ogni c in I vale l'eguaglianza.
Portando al primo membro fy, la condizione diventa
y ' (x) - f(x) y (x) = 0 per ogni x in I
si cerca di tramutare il primo membro nella derivata di una funzione z(x) in modo da ridursi a
z ' (x) = 0 per ogni x in I. Questo si ottiene moltiplicando per e^{-F(x)} ove F '(x) = f(x) su I
e^{-F(x)} y ' (x) - e^{-F(x)} f(x) y (x) = 0 per ogni x in I
ma ora il primo membro e' la derivata di e^{-F(x)} y(x), quindi come si voleva la condizione diventa:
(e^{-F(x)} y(x)) ' = 0 per ogni x in I
quindi e^{-F(x)} y(x) deve essere costante sull'intevallo I, cioe'
e^{-F(x)} y(x) = k per ogni x in I
cioe' una soluzione se c'e' deve essere dela forma
y(x)= k e^{F(x)} x in I, ove k e' una qualsiasi costante e F'= f su I.
Derivando si ottiene che in effetti le funzioni di questa forma sono soluzioni dell'equazione differenziale di partenza. Quindi sono le sole soluzioni.
Ricordando il teorema fondamentale del calcolo integrale ogni F per cui F ' =f e' , del tipo
F(x)= Integrale da p a x di f(t) dt . Quindi se f e' continua le soluzioni di
y '(x)= f(x) y (x) per ogni x in I
sono le funzioni nella variabile x: y(x)= k e^{ Integrale da p a x di f(t) dt}
Dati un numero S e q in I, se si impone oltre a: y '(x)= f(x) y (x) per ogni x in I
anche la condizione ``di passaggio'': y(q)= S
allora tra le soluzioni dell'equazione differenziale ve n'e' solo una che soddisfa l'ulteriore condizione ottenuta in modo che la costante k soddisfi la relazione :
k e^{ Integrale da p a q di f(t) dt}=S
Se si interpreta x come tempo, y come posizione e quindi y' come velocita' istantanea
questo dice che se conosco la velocita' in termini dell'istante e della posizione
vi e' un unica traiettoria che all'istante q passa per la posizione S.
5-12-08 lezione 22 (Tortorelli) Le seguenti note sono esplicative rispetto allo schema presente nel file allegato:
. APPUNTI SU EQUAZIONI DIFFERENZIALI.
1) Equazioni differenziali
del primo ordine
in forma normale
lineari
non omogenee
data A(x) continua su un intervallo I trovare J intervallo in I e una funzione derivabile su J per cui
y'(x)= A(x) y(x) + f(x), p.o. x in J
- A(x)=0 teorema fondamentale del calcolo se p in I: y(x) = integrale da p a x di f(t) dt
- fattore integrante e formula di ``semigruppo'':
*************** il metodo del fattore integrante e' IMPORTANTE ***************
si porta Ay al primo membro
si moltiplica per e^{- integrale da p a x di A(s) ds}
il primo membro e' derivata di y(x) e^{- integrale da p a x di A(s) ds}
si integra tra p e x usando al primo membro il teorema fondamentale del calcolo
si porta al secondo membro y(p)
si moltiplica per e^{integrale da p a x di A(s) ds}
si ottiene che se c'e' una soluzione y(x) dve essere
y(x)=
= e^{integrale da p a x di A(s) ds} y(p) +
+ e^{integrale da p a x di A(s) ds} int.da p a x di ( e^{- integrale da p a t di A(s) ds}f(t))dt =
= e^{integrale da p a x di A(t) dt} + int.da p a x di ( e^{- integrale da x a t di A(s) ds}f(t))dt
si verifica che tutte le funzioni di questo tipo sono soluzioni:
il primo addendo e' una generica soluzione dell'equazione omogenea
il secondo addendo e' una soluzione particolare dell'equazione completa
************************* Importante ***********************************
- Metodo della ``variazione della costante'' per calcolare una soluzione particolare:
si trova una soluzione non nulla dell'omogenea u(x): u'=Au
si cerca v(x)=c(x) u(x) , con c(x) funzione incognita, che soddisfi v'= Av +f
v' = c' u + c u' si mette nell'equazione
c' u + c u' = A cu + f
ma per scelta u'=Au quindi c'u =f , quindi c' =f/u quindi c(x) e' una qualsiasi primitiva
di f/u con u'=Au
In effetti nella formula di semigruppo il secondo addendo e' proprio la funzine integrale di
e^{- integrale da x a t di A(s) ds}f(t)= f(t)/ e^{integrale da x a t di A(s) ds}.
esempio a caso
y'= x y +x^2 calcola calcola calcola .... c'(x)= x^2 e^{-x^2/2} .... e' andata male
infatti
x^2 e^{-x^2/2} = - x ( e^{- x^2/2} )' =e^{- x^2/2} - ( x e^{- x^2/2} )' quindi
c(x) = primitiva di e^{- x^2/2} - x e^{- x^2/2}
ma la primitiva di e^{- x^2/2} non si sa calcolare simbolicamente!
-Tutte le soluzioni sono del tipo: soluzione particolare + soluzione qualsiasi dell'omogenea
- problema di Cauchy ed unicita' :
************* IMPORTANTE ricordarsi che c'e' unicita' per il problema di passaggio*****
dato p in I e un valore q la funzione y(x) =
= q e^{integrale da p a x di A(t) dt} + int.da p a x di ( e^{- integrale da x a t di A(s) ds}f(t))dt
e' l'unica soluzione di
y'(x)= A(x) y(x) + f(x), p.o. x in I
y(p) = q
- Altro modo di vedere il secondo addendo della formula di semigruppo:
principio di sovrapposizione degli effetti di Duhamel dovuto alla linearita'
si pensa che l'impulso f(x) dato istante x per istante x alla velocita' y'(x) si possa ottenere
come ``somma infinita'' (integrale) di moti omogenei che all'istante t valono f(t):
( y_t )' (x) = A(x) y_t(x)
y_t (t) =f(t)
per quanto detto la lezione scorsa y_t (x)= e^{integrale da t a x di A(s) ds}f(t)
``sommando'' (integrando) rispetto a t si ottiene proprio il secondo addendo.
- L'insieme delle soluzioni dell'omogenea e' uno spazio vettoriale di dimensione 1:
se y e z sono soluzioni e m e' un numero:
*******************IMPORTANTE******************************
cioe' somma di soluzioni di un'equazione lineare omogenea e prodotto per un numero e ' soluzione
(y(x) +m z(x))' = y' + m z' = Ay + m Az = A(y+mz)
Si consideri C^1= spazio vettoriale delle funzioni derivabili con derivata continua su I
C = spazio vettoriale delle funzioni continue su I
L : C^1 ----> C trasformazione cosi definita L(g) =g' -A (alla funzione g(x) si associa la funzione g'(x) -A(x)g(x) )
L e' un operatore differenziale del primo ordine
il suo nucleo Ker L ={ g: Lg=0 }e' lo spazio vettoriale delle soluzioni dell'equazione omogenea
L'equazione differenziale non omogenea si scrive L(y) = Ay +f
Se v e' una soluzione particolare l'insieme delle sue soluzioni e ' quindi il traslato per v di KerL
v+Ker L
*****************la seguente scaletta e' IMPORTANTE*********************
-Scaletta oltre alla formula data un metodo abbastanza generale e pratico e' il seguente:
i - si trova (come si riesce si riesce) una base dello spazio vettoriale delle soluzioni dell'omogenea
k u(x) u'=Au u non identicamente nulla
ii - si trova una soluzione particolare v
a tentativi,
o con ricette particolari,
o con il metodo della variazione delle costanti arbitrarie:
(v(x)=c(x) u(x) , c(x) funzione incognita da trovare imponendo che v sia soluzione)
iii - si trova il coefficiente k per cui
ku(p) +v(p) = q
questa scaletta vale per tutti le equazioni e sistemi differenziali lineari solo che in questi casi piu' generali lo spazio delle soluzioni dell'omogenea puo' avere dimensione d maggiore di 1
e quindi:
i- k_1 u_1(x) + ... + k_d u_d(x), u_j ' =A u_j e u_1... u_j linearmente indipendenti
ii- v(x) del tipo c_1(x) u_1 (x) + ... c_d(x) u_d(x)
iii- trovare k_1, ... k_d per cui le condizioni di passaggio siano verificate.
2) Un po di terminologia generale:
- Equazioni e sistemi differenziali ordinari di ordine n:
data F(x, p, q_1 , ... , q_n) a valori in R^k (F=(F_1 ... F_k))
definita per x in I intervallo, p , q_1 ... q_n ognuno in qualche sottoinsieme di R^m
il sistema (se k=1 l'equazione ) ordinario associato e'
F(x, y(x), y' (x), y'' (x) ... y^(n) (x)) = 0
- Forma normale :
se k=m e F(x,p, q_1 ,... q_n) = G(x,p, q_1 ,... q_{n-1}) - q_n . Il sistema diventa :
y^(n) (x) = G(x, y(x), y' (x), y'' (x) ... y^(n-1) (x))
- Equazioni e sistemi lineari in forma normale:
se per ogni x (p, q_1 ...q_n ) ----> G(x,p, q_1 ,... q_{n-1}) e' lineare con una eventuale traslazione
cioe' se G(x,p, q_1 ,... q_n) = M(x) prodotto righe per colonne (p, q_1 ,... q_{n-1}) + T(x)
con M(x) matrice di funzioni m righe x m n colonne e T(x) vettore di funzioni con m componenti T(x)= (T_1(x) ,... T_m (x)). Il sistema diventa
derivata ennesima di y in x = M(x) prodotto righe per colonne (y(x), y'(x) ,... y^(n-1)(x)) + T(x)
e l'eguaglianza va intesa come sempre componente per componente.
- Equazioni e sistemi lineari in forma normale omogenei: se T e' nullo.
-Enunciato del teorema di Cauchy Lipschitz (esistenza locale ed unicita'):
Se G e' continua in ognuna delle sue variabili, e ha derivate rispetto alle tutte le mn variabili diverse da x che siano funzioni limitate indipendentemente da x
se (r, s, v_1, ...v_{n-1}) e' un punto interno a dove G e' definita allora
esiste un intervallo J contenente r
esiste una funzione y(x) derivabile n volte su J
y^(n) (x) = G(x, y(x), y' (x), y'' (x) ... y^(n-1) (x))
y(r) = s
y'(r) = v_1
y''(r) = v_2
...
...
y^(n-1) (r) = v_{n-1}
inoltre questa e' l'unica funzione che soddisfa le condizioni date e il sistema differenziale.
Aggiungendo ipotesi si ottiene di piu' , per esempio la cosi detta esistenza globale:
se G (x, p, ...) e' definita per ogni x in R ed e' una funzione limitata allora la soluzione y e' definita su tutto R.
**********questi controesempi sono piccoli esercizi per impratichirsi anche se descrivono ``anomalie'' *************************************************************
Esempio: y'(x) = y^2(x) y(0)=3 (non esistenza per tutti i tempi)
m=1, n=1, G(x,p) = p^2 definita su tutto R^2, r=0, s=3
se c'e' una soluzione non e' sempre nulla per la condizione y(0)=3
e rimarra' vicina a 3 per x vicino a 0
per cercarla dividiamo per y^2 l'equazione
y'(x)/y^2(x) =1
ma il primo membro e' la derivata in x di - 1/y(x) quindi passando alle primitive
-1/y(x) = x + c
dovendo essere y(0)=3 allora c deve essere -1/3
1/y(x) = 1/3-x quindi
y(x) = 1/(1/3 -x)
Derivando si ottiene che in effetti tale y(x) e' soluzione del problema ma ....
... non e' definita su tutto R !
Il grafico di y ha asintoto verticale in x=1/3.
Se vedo y(x) al variare di x come moto unidimensionale sull'asse verticale,
e' un moto che al tempo x=1/3 e' ``schizzato all'infinito''.
Dopo l'istante 1/3 non c'e' piu' niente.
In effetti G(x,p)=p^2 non e' limitata.
Esempio: y'(x) = radice di |y(x)| y(0)=0 (non unicita' del problema di Cauchy)
m=1, n=1, G(x,p) = radice di |p| definita su tutto R^2, r=0, s=0
z(x)= 0 per ogni x in R e' una soluzione
ma pensiamo un po ... piu' o meno g(x)=x^2 ha una derivata g'(x)=2x che almeno per gli x non negativi e ' proporzionale alla sua radice ...
vediamo se ci sono soluzioni del tipo y(x) = a(x-c)^2, a>0 , x>c e y(x)= 0 per x<0; deriviamo
y'(x)= 2a(x-c) per x>c, y'(0)= 0, y'(x) =0 per x<c
sostituiamo nell'equazione differenziale per vedere se per qualche a e' soddisfatta:
2a(x-c) = radice di a |x-c| per x>o= c
0=0 per x<c
se ne deduce che 2a =radice di a cioe' a = 1/4.
Uhuh .... tutte le funzioni y(x) = 1/4 (x-c)^2 per x>c>0 e zero prima di c
sono sia soluzioni dell'equazione che della condizione.
Infinite soluzioni del problema di passaggio per un punto fissato a tempo fissato!
- Equazioni del primo ordine come cinematica unidimensionale:
interessano i grafici (delle soluzioni) nel piano delle leggi orarie
Interpretazione con tassi di accrescimento istantanei: decadimento radiottivo, crescita con risorse illimitate di una popolazione senza antagonisti ....
***************MA .... ATTENZIONE ***************************************
- Sistemi del primo ordine come cinematica bidimensionale:
interessano le traiettorie (immagini delle soluzioni) nel piano dei moti
Interpretazione geometrica dato un vettore V (p) in ogni punto p trovare una famiglia di curve
che copre il piano che in ogni punto abbia quel vettore come tangente
e.g. V(x,y)=(x^2-y, x+y^2) basta senz'altro trovare
x'(t)= x(t)^2 - y(t)
y'(t)= x(t) + y(t)^2
Altra interpretazione non esplicitata a lezione evoluzione nel tempo di due popolazioni> Esaminiamo a grandi lineee il caso lineare, molto riduttivo, realistico sotto ben precise assunzioni:
x'(t)= x(t) - y(t) - t
y'(t)= 2 x(t) + 3 y(t) + t^2
la popolazione x lasciata a se stessa incrementa egualmente alla quantita' presente
e diminuisce (emigrazione) di t
in piu' e' contrastata dalla presenza della popolazione y
che a sua volta ha un tasso di variazione istantaneo pari al triplo della sua quantita' e aumenta di t^2 (immigrazione) e si giova della presenza di x per il doppio
E' un modello preda predatore.
Se fosse stato
x'(t)= x(t) - y(t)
y'(t)= - 2 x(t) + 3 y(t)
sarebbe stato un modello di competizione, e con tutti segni positivi un felice matrimonio
... modello di simbiosi.
Sistema lineare generale ... chi sa se avremo tempo di studiare come sono fatte le immagini delle soluzioni .... almeno nel caso di coeficienti costanti
x'(t)= a(t) x(t) + b(t) y(t) + f(t)
y'(t)= c(t) x(t) +d(t) y(t) + g(t)
- Equazioni del secondo ordine come dinamica:
determinismo meccanico:
e' il principio fisico che si formalizza ed astare nel teorema di Cauchy-Lipschitz:
*****************IMPORTANTE******************************************
note le forze in dipendenza dal tempo dalla posizione e dalla velocita' e note posizione e velocita' in un certo istante tutto il moto e' determinato.
y''(t) = F(t, y(t), y'(t))
y(r) =s
y'(r) = v
sotto le ipotesi dette ha un unica soluzione.
******************QUI SOTTO CI SI TORNA SOPRA*************************
Equazioni del secondo ordine lineari (oscillatori):
quindi il problema di Cauchy seguente con m(t) continuo e mai nullo, e A, B, C continue
m(t) y''(t) = A(t) y(t) + B(t) y'(t) + C(t)
accellerazione per massa = forza elastica (campo conservativo) + forze tipo attrito + forze esterne
ha sempre un ' unica soluzione
e qui ci potra' essere risonanza.
**********************RICORDARE**********************************
- Equazioni a variabili separabili y'(x)= f(x) g(y(x))
gli zeri di g sono i valori delle soluzioni costanti
quindi in ricerca di soluzioni che non sono costanti senza entrare nel dettaglio (vedi appunti)
dovra' essere per qualche intervallo U g(y(x)) non 0 per x in U
quindi y'/g(y(x)) =f(x)
se so calcolare una primitiva S di 1/g(p) in qualche intervallo J ove g non si annulla
se so trovare un intervallo I, una primitiva F di f su I
per cui F(x) sta nell'immagine di g su J
allora la soluzione deve avere grafico contenuto in {(x,p) : F(x)=S(p)}
quindi se so disegnare quel sottoinsieme del piano gia' molto ricavo.
se poi ``so calcolare '' l' inversa di S riesco ad esprimere la soluzione con una formula
y(x)= S^{-1}(F(x))
****************RICORDARE ******************************************
Equazioni autonome sono particolare equazioni a variabili separabili: y'(x) = g(y(x))
gli zeri di g sono i valori di soluzioni costanti
quindi trovata una soluzione u(x) con grafico compreso tra le due rette orizzontali alla quota di due tra gli zeri di g
tutti grafici delle altre soluzioni comprese tra questi due zeri si ottengono traslando in orizzontale il grafico dato
quindi data una soluzione u tra due zeri di g tutte le altre tra questi due zeri sono del tipo u(x+c)
infatti d u(t+c)/dt = du/dt (x+c) =g (u(x+c)).
e.g. y'(x) = y(x)(1-y(x)) da terminare.
Riferimenti:
[EB] cap. 11 pagg. 334-352, 361-362, 364-366, 373-375;
[MA1] cap.8 pagg. 340- 343, 347-353, 356-358, 363-364;
[BDM] cap.6 pagg.218-222, cap. 8 pagg. 331-346;
[IRS] cap. 6 pag. 225-228, pagg. 230-232;
[VV] cap.9 pagg. 197-198, 201-208.
9-12-08 lezione 23 recupero (Tortorelli) Nella seguente lezione oltre ad esporre gli schemi teorici si sono svolti quattro esercizi.
Le seguenti note sono in fase di redazione ed esplicative rispetto allo schema presente nel file allegato:
. APPUNTI SU EQUAZIONI DIFFERENZIALI.
1) Variabili separabili: y'(x)=g(y(x)) f(x) f continua su A intervallo, g continua su B intervallo.
- per lo schema metodologico vedere appunti
- gli zeri di g corrispondo a soluzioni costanti
le rette orizzontali di grafici di tali soluzioni costanti nel caso
in cui g abbia derivata continua introno a tali zeri sono
asintoti orizzontali
per le soluzioni non costanti
- Se |g(p)| < a|p| +b intorno a +oo [risp. -oo] allora le soluzioni hanno domini del tipo
semirette illimitate superiormente [risp. inferiormente]
il seguente esempio mostra che le rete orizzontali possono essee toccate da altre soluzioni (mancanza di unicita') quando g non ha derivata limitata, e che le soluzioni non costanti possono non essere definite su tutto R quando |g(p)| si compoorta come |p|^{1+k}
y'(x)=radice quadrata di y(x) (1-y(x)) x^2
2) Equazioni autonome esempio svolto
y'(x)=y(x)(1-y(x))
3) Equazioni differenziali
del secondo ordine
lineari
non omogenee
date a(t), b(t), c(t), f(t) continue su un intervallo I, a(x) mai nulla su I, trovare le funzioni derivabili su I per cui:
a(t)y''(t)+ b(t) y'(t)+ c(t) y(t) =f(t)
Problema di Cauchy: eventualmente dato q in I trovare l'unica tra le soluzioni per cui
y(q) = y_0
y'(q) = y_1
La scaletta e' la solita:
i- trovare tutte le soluzioni dell'omogenea
Teorema: le soluzioni dell'equazione omogenea sono uno spazio vettoriale di dimensione 2
quindi date due di esse linearmente indipendenti (una base dello spazio)
u_1(t), u_2(t), tutte le altre soluzioni u(t) sono del tipo
u(t) =A u_1(t) +B u_2(t) al variare dei numeri A e B
Teorema: se u_1(t), u_2(t) sono una base dello spazio delle soluzioni
la matrice di funzioni con colonne (u_1(t), u_2(t) ) e (u_1 ' (t), u_2 ' (t) )
ha sempre determinante non nullo quindi ha inversa.
ii- soluzione particolare u^*
si trova o per tentativi
o con il metodo delle costanti arbitrarie
o con altri metodi per articolari termini noti
iii- tutte le soluzioni della non omogenea saranno del tipo
y(t) = u^*(t) + A u_1(t) +B u_2(t) al variare dei numeri A e B
solo a questo punto si scelgono le costanti A e B perche' siano soddisfatte le eventuali condizioni del problema di Cauchy
4) Equazioni differenziali
del secondo ordine
lineari
a coefficienti costanti
non omogenee
e' il caso particolare in cui a(t)=a non 0, b(t)=b, c(t)=c costanti.
ay''(t)+ b y'(t)+ c y(t) =f(t)
In questo caso il passo i) cioe' la risoluzione dell'omogenea si puo' fare facilmente e quindi dimostrare il teroema enunciato
a) punto da fare nella pratica:
si prende il polinomio az^2 +bz +c
si trovano le sue radici complesse r_1, r_2 , quindi az^2 +bz +c =a (z-r_1)(z-r_2)
quindi si osserva che
b= - a(r_1 +r_2)
c= a r_1r_2
*************************RICORDIAMO **********************************
per trovare le radici di az^2 +bz +c si usa la solita formula
se w_1 e w_2 sono le due radici quadrate complesse del discriminante b^2- 4ac
allora
r_1 = (-b +w_1)/2a , r_2 = (-b +w_2)/2a
***********************************************************************
b) punto solo teorico:
per cui una funzione u e' soluzione di
a u''(t)+ b u'(t)+ c u(t) =0
se e solo se (si sostituisce a z l'operazione di derivazione)
a u''(t)+ b u'(t)+ c u(t)= (d/dt -r_1)( (d/dt -r_2) u(t))=0
cio' e' equivalente a
u'(t) - r_2 u(t)= v(t)
v'(t) - r_1 v(t) = 0
ma allora dalle formule viste le precedenti lezioni
v(t)= k_1 e^{r_1 t}
u(t) = k_2 e^{r_2 t} + e^{r_2 t} integrale da 0 a t (e^{-r_2 s}k_1 e^{r_1 s})ds
due casi:
c)
*) r_1 =r_2 = r allora l'integrale diventa l'integrale di 1 quindi
u(t) = k_2 e^{rt} + k_1 t e^{rt}
**) r_1 diverso da r_2 l'integrale e ' 1/(r_1-r_2)( e^{(r_1-r_2)t} -1 ) quindi
u(t) = k_2 e^{r_2 t} + k_1e^{r_1t}/(r_1-r_2) - k_1e^{r_2t}/(r_1-r_2) =
= c_1 e^{r_1 t} + c_2 e^{r_2 t}
d) se a , b , c sono numeri reali si desiderano numeri reali
ora
i- az^2 +bz +c o ha due soluzioni reali distinte r_1 non = r_2 (discriminante>0)
tutte le soluzioni reali sono, come detto in **) prendendo i coefficienti reali, del tipo:
A e^{r_1 t} + B e^{r_2 t} , al variare di A e B numeri reali
ii- az^2 +bz +c o ha una soluzione reale ``doppia'' r, cioe' e' a(z-r)^2 (discriminante nullo)
tutte le soluzioni reali sono, come detto in *) prendendo i coefficienti reali, del tipo:
A e^{rt} + B t e^{rt} , al variare di A e B numeri reali
iii- az^2 +bz +c o non zlcuna soluzione reale ``doppia'' r, cioe' ha due soluzioni complesse
una coniugata dell'altra p+ i q e p-iq (discriminante negativo)
in questo caso si usa **) con c_1 e c_2 eguali prima ad A/2 , A/2 e poi - iB/2, i B/2
e soi ottiene che tutte le soluzioni reali sono del tipo
A e^{p t} cos q t + B e^{p t} sin q t , al variare di A e B numeri reali
( e^{ivt}+e^{-ivt} = 2 cos vt , -i e^{ivt}+ie^{-ivt} = 2 sin vt )
5) dimostrazione del metodo della variazione delle costanti
che si applica anche quando i coefficienti non sono costanti quando si sappiano le soluzioni dell'omogenea
data una base dello spazio delle soluzioni dell'omogenea u_1(t), u_2(t)
si cerca una soluzione u^* della non omogenea del tipo c_(t) u_1(t) +c_2(t) u_2(t)
per trovare c_1(t), c_2 (t) si fanno le derivate e si sostituiscono nell'equazione
a(t)y''(t)+ b(t) y'(t)+ c(t) y(t) =f(t)
si ottiene che deve essere
a(t)(( c_1 ' u_1 + c _2 ' u_2 )' +c_1 ' u_1' + c _2 ' u_2 ') + b(t)(c_1 ' u_1 + c _2 ' u_2 ) = f(t)
a questo punto il metodo canonico e' imporre che il coefficiente di b(t) sia nullo per cui si ha il sistema numerico t per t:
c_1 ' u_1' + c _2 ' u_2 ' = f/a
c_1 ' u_1 + c _2 ' u_2 = 0
con incognite c_1 ' (t) e c_2 ' (t) e coefficienti u_1' (t) , u_2' (t) ,u_1(t) ,u_2(t) , f(t)/a(t)
che per quanto detto nel teorema precedente si puo' sempre risolvere
quindi si trovano le derivate dei coefficienti di u^* (t) se si sanno fare le primitive allora
si trova esplicitamente la soluzione particolare
Esempio svolto: y''(t) -y(t) = cos t
la base dell'omogenea e' data dalle funzioni e^t ed e^{-t}
il sistema diventa c_1 ' e^t - c_2 ' e^{-t} = cos t
c_ ' e^t + c_2 ' e^{-t} = 0
per cui c_1' = 1/2 e^{-t} cos t
c_2 ' = -1/2 e^{t} cos t
facendo per ogni eguaglianza due integrazioni per parti si ottiene
c_1 = e^{-t}/4 (sin t - cos t)
c_2 = e^{t} /4 ( sin t + cost)
per cui una soluzione particolare e' u^*(t) = 1/2 sin t
6) nel caso di equazioni a coefficienti costanti si puo' usare anche il metodo dei coefficienti indeterminati per termini noti di tipo particolare (vedere appunti)
Esempio svolto: y''(t) +y(t) = cos t
le radici di z^2 +1 sono i e -i cioe' 0+ i 1 e 0 - i1
il termine noto e' e^{0t} ( 1 cos 1t + 0 sin 1t) quindi la soluzione deve essere del tipo
A cos t + B sint
per trovare A e B si fanno le derivate si sostituisce nell'equazione e si trovano le codnizioni su A e B
Fenomeno di RISONANZA
u''(t) + u(t)=0 ha la sola soluzione limitata u(t) = cos t + sin t
u(0)=1
u'(0)=1
se pero' `` marcio con ritmo pari alla frequenza propria''
y''(t) +y(t) = cos t ottengo che la soluzione che si amplifica sempre di piu'
y(0)=1 y(t) = cos t + sin t +t/2 sin t
y'(0)=1
.l9-12-08 esercitazione 12 recupero (Mauro) Esercizi: integrali di funzioni non limitate su intervalli illimitati, numeri complessi, equazioni differenziali
11-12-08 lezione 24 (Tortorelli) Sommatoria: definizione, esempi, linearita', gli integrali come limiti di sommatorie, le sommatorie come integrali di funzioni costanti su segmenti unitari nel caso finito o nel caso
di segno costante, divergenza della serie armnica con confronto di integrali, serie di ragione 1/n^a.
Breve introduzione:
organizzazione, manipolazione e semplificazione e esposizione di dati ---> statistica descrittiva
semplificare problemi di conteggio ..... ---> calcolo combinatorio
||
operare con rigore su dati e previsioni incerti .... ----> calcolo delle probabilita' nel caso finito
metodi per estrapolazioni da campionature e valutazione del rischio .... ----> statistica inferenziale
dati qualitativi, quantitativi (vettoriali), discreti continui
modalita'
carattere o nel caso discreto e quantitativo variabile aleatoria
dato come realizzazione di un carattere
dati continui
mediana, quantili, range
diagrammi a barre
discretizzazione di caratteri continui
diagrammi (esempio sulle altezze dei presenti in aula)
calcolo della media con le frequenze relative
calcolo della media su dati che non inducono una partizione sulla popolazione (esempio: su un totale di 90 studenti 19 danno il primo esame, 23 il secondo e 54 il terzo: calcolare il numero medio di esami sostenuti per studente)
notazione vettoriale per la media
.l2-12-08 esercitazione 13 (Mauro) Esercizi su integrali ed equazioni differenziali.
15-12-08 lezione 25 (Tortorelli)
Frequenze per relazioni che non sono funzioni (dati che non inducono una partizione sulla popolazione, ovvero dati che non sono la realizzazione di un carattere).
Esempio di dati che permettono di calcolare la media ma non mediana: modifica dell'esempio della precedente lezione su un totale di 61 studenti 19 danno il primo esame, 23 il secondo e 54 il terzo:
si considera la distrubuzione ``cumulativa'' in cui gli studenti che hanno sostenuto un esame hanno sostenuto anche gli esami con maggiori frequenze assolute, la si modifica in maniera compatibile con i dati in modo che la mediana da 1 diventi 2.
Esempio di calcolo della media con frequenze relative (date le percentuali, rispetto alla popolazione incognita dei clienti, dei numeri d'ordine di certi beni, e dati gli importi medi per ordine nelle varie fasce percentuali, calcolare la media di numero d'ordini per cliente, e quindi l' importo medio per ordine sul totale).
Proprieta' astratte della media:
linearita': media (v + p w) = m(v) + pm(w)
in particolare m(x_1+c, x_2+c ... , x_N +c) = m(x_1 ... x_N) + c
Varianza e sua interpretazione geometrica:
Var(x) = m( x_1^2 , ... x_N^2) -(m(x))^2
notazione vettoriale per la varianza Var(x) = 1/N || x- (m, ..., m)||^2 = 1/N somme su i (x_i-m)^2
Scarto quadratico medio o deviazione standard
sigma (x) = radice quadrata di Var(x)
Esempio di dati che permettono di calcolare la media ma non la varianza (dati che non inducono una partizione).
Proprieta' di minimo della media e della varianza:
la media m(x) e' il punto di minimo di V(y)= 1/N somme su i (x_i-y)^2
la varianza Var(x) e' il valore di minimo di V(y) (dimostrazione per quadratura).
Proprieta' astratte della varianza
Var(px) = p^2 Var (x)
Var (v+w) = Var (v) + Var (w) - 2 1/N (v-(m(v), ..., m(v)) ).(v-(m(w), ..., m(w)) )=
= Var (v) + Var (w) - 2 1/N somme su i (v_i - m(v))(w_i - m(w))
in particolare
Var (x_1+c, ..., x_N +c) = Var (x)
Covarianza
Cov(v,w) = 1/N (v-(m(v), ..., m(v)) ).(v-(m(w), ..., m(w)) ) =
= 1/N somme su i (v_i - m(v))(w_i - m(w)) =
= media dei prodotti (v_iw_i) - prodotto delle medie m(v) m(w)
Correlazione: normalizzazione della covarianza Cov(x,y)/ (sigma(x)sigma (y)) grazie all'interpretazione geometrica non e' altro che il coseno dell'angolo tra i vettori dei datI:
x= (x_1 ... x_N) e y= (y_1 ... y_N)
sara' sempre tra -1 e 1.
Minimi quadrati rette di regressione ed interpretazione della dipendenza tra coppie di dati
15-12-08 lezione 26 recupero (Tortorelli)
Non negativita' della varianza dedotta dalla diseguaglianza di Cauchy-Schwarz.
Scala logaritmica e doppiamente logaritmica: rette di regressione per indagare dipendenze di tipo esponenziale e di tipo potenza.
Osservazione su dati negativi per applicare le scale logaritmiche.
Problema non matematico: vi e' un fondamento fisiologico sull'efficacia del metodo dei minimi quadrati rispetto a valutazioni qualitative della retta che ``meglio si adatta'' ad una distribuzione
di punti nel piano? (Invito a fare esperimenti personali ed indagine presso i docenti competenti nel settore).
15-12-08 esercitazione 14 recupero (Tortorelli) Esempio di calcolo di retta di regressione su sei coppie di dati numerici. Commenti relativi ed impostazione del calcolo per scale logaritmiche.
18-12-08 lezione 27 (Tortorelli)
INTRODUZIONE AL CALCOLO DELLE PROBABILITA'
Riferimenti: Si consigliano le letture degli esempi esposti nei vari libri consigliati.
Per quanto riguarda l'approccio e l'impostazione generale, pur avendo delle profonde
differenze sull'ordine di presentazione e sulla rilevanza da dare ai diversi concetti teorici,
senza dubbio e' da preferire per chiarezza e completezza:
[MA1] cap.2 pagg. 35-61, 69-80 , cap. 7 pagg.301-315, 320-326;
Problema
Dare senso rigoroso ed introdurre regole di calcolo per trattare domande del tipo
con che probabilita' un accadimento casuale si realizza con certe modalita'
qual'e' il valore medio di una grandezza casuale ...
Data una grandezza aleatoria Y (concetto intuitivo)
0- per prima cosa individuare dove certamente assume i suoi valori:
rappresentiamo questo ambito di variazione di Y con un insieme V
1- dal singolo problema oggetto di studio saranno di interesse certe eventualita'
esprimibili con frasi del tipo ``Y sta in H'' con H che varia tra certi sottoinsiemi di V
chiamiamo questa famiglia di ``eventaulita''' interessanti H
sembra utile a priori, o per lo meno comodo, avere l'evento impossibile ``Y sta nell'insieme vuoto'' e l'evento sicuro ``Y sta in V''
d'altronde si vuole poter valutare eventualita' composte del tipo ``Y sta in H ma non in K'' eccetera eccetera
Si tratta quindi di trovare una famiglia F di sottoinsiemi di V per cui
i- vuoto e V stanno in F i-bis (ipotesi non matematica ma dettata dal problema) F contiene H
ii- se A e B stanno in F allora AU B, A intersezione B, A\B stanno in F.
iii- (ipotesi decisamente matematica) se A_n n in N e' una successione di elementi di F
allora la loro unione sta in F.
Una famiglia che soddisfa i, ii si dice algebra di sottoinsiemi di V
se verifica anche iii si dice tribu' osigma-algebra .
(V,F) si dice spazio misurabile.
Eventi incompatibili, famigli di eventi esaustivi ed incompatibili, eventi elementari.
Esempi: Y lancio di una moneta, Y lancio di un dado, Y misura dell'altezza di un individuo preso a caso in una popolazione, Y scelta casuale di un punto su un segmento.
Nei casi in cui Y a priori puo' assumere un numero finito di valori F sara' usualmente l'insieme di tutti i sottoinsiemi di V.
Ma non sempre cio' e' ragionevole sia per poter usare strumenti matematici potenti, si per economia concettuale rispetto al problema concreto che stiamo idealizzando: conviene che F sia la piu' piccola tribu' conetnento il dato H.
2- Si vuol dare senso, ed assegnargli un valore numerico,
al termine la ``probabilita' che Y stia in A'' per gli A in F.
Dal singolo problema oggetto di studio per le eventualita' interessanti di H sara' assegnato
un valore d(H) alla ``la probabilita' che Y sta in H'', o comunque si faranno ipotesi su come assegnare queste probabilita' (per esempio basandosi su dati staistici o su leggi precedentemente note etc. etc. salvo poi falsificarle basandosi su nuovi esperimenti etc. etc. siamo al cuore del metodo scientifico poche parole per anni di lavoro).
Comunque il nocciolo matematico e' che tali assegnazioni d(H), per H in H, dovranno
potersi estendere ad F in modo compatibile con le regole che esporremo ora.
Si considera una funzione m : F --> [0;1] per cui
0- 0 <o= m (A) <o= 1
i- m(vuoto)=0, m(V)=1 i-bis m(H)= d(H) per H in H ,
ii- m(AUB)= m(A)+ m(B) -m (A intersezione B)
iii- Se A_n e' una successione di elementi di F a due a due disgiunti dve essere
m(U {A_n : n in N} )=
serie m(A_n) = lim_{N -->+oo} m(A_1) + m(A_2) + ... +m(A_N)
Una tale funzione si dice distribuzione, o misura, o legge di probabilita' su (V, F)
(V, F, m) si dice spazio di probabilita'.
Monotonia rispetto all'inclusione.
Passaggio al limite su successioni monotone rispetto all'inclusione.
Quando il dato H e' abbastanza ricco e d(H) soddisfa le regole date m e' univocamente determinata. In tal caso e' bene chiamarla legge di probabilita' di Y.
Quindi si pone ``probabilita' che Y stia in A''= m(A) per gli A in F.
Tale m e' il principale oggetto su cui fare i calcoli.
Esempi: casi favorevoli su casi possibili, frequenze relative ...
2-bis (Kolmogorv) Per fini molto spesso teorici avendo piu' di un evento aleatorio Y e' comodo rappresentare contemporaneamente diversi eventi aleatori come particolari funzioni definite sullo stesso dominio B.
Si anticipa che in molti casi cio' e' inutile se non dannoso: cio' che serve e' m.
D'altronde in altri casi , specialmente quando V e' un insieme finito, e' comodo solo pensare
a questa base comune, e Y ``sparira' '' diventando la funzione identica su B=V.
Lo si fa usando i seguenti concetti:
(Richiamo delle proprieta' della preimmagine di una funzione rispetto ad unione, intersezione e complemento)
i- Siano (B, G) e (V,F) due spazi misurabili
una funzione X:B--> V si dira' variabile aleatoria se
{ b in B: X(b) in A} brevemente {X in A} sta in G per ogni A in F
ii- Siano (B, G, P) e (V,F, m) due spazi misurabili e X una variabile aleatoria dal primo al secondo.
Diremo che m e' la legge di probabilita' di X (indotta da P) se
P{X in A} = m(A) per ogni A in F.
Quindi sotto opportune condizioni un teorema di Kolmogorov garantisce
che data una famiglia di accadimenti casuali Y
ognuna con le sue leggi di probabilita' m_Y su certi V_Y
si puo' trovare uno stesso spazio di probabilita'
(B, G, P) e una famiglia di variabili aleatorie X_Y a valori ognuna nel rispettivo (V_Y, F_Y)
in modo che le leggi m_Y date dal lavoro scientifico siano le leggi rispettivamente
delle variabili aleatorie X_Y.
In questo senso la variabile aleatoria X_Y :(B, G, P) --> ( V_Y, F_Y , m_Y)
rappresenta l'accadimento casuale Y. Si sottolinea che il fatto notevole
e' farlo in ``blocco'' per intere famiglie (anche infinite) di accidenti Y con uno stesso spazio ``base'' di probabilita' (B, G, P).
Esempi: (dove si vede quanto si trascura (B, G,P) o quanto si trascura Y) lancio di monete,
lancio di dadi, legge di Mendel nel caso di dati genitori e due alleli, distribuzione uniforme sul finito, distribuzione pesata sul finito.
Eventi indipendenti (rispetto ad una legge di probabilita) variabili aleatorie indipendenti.
Schema di Bernoulli
Un po di calcolo combinatorico: unioni disgiunte, prodotti cartesiani, funzioni e disposizioni con ripetizione, funzioni iniettive e disposizioni semplici, coefficienti binomiali e combinazioni senza ripetizione sottoinsiemi di cardinalita' data, combinazioni con ripetizione, binomio di Newton, relazione ricorsiva per i binomiali (metodo del testimone)
Densita' di una variabile aleatoria discreta
Distribuzione binomiale
interpretazione della binomiale:
k successi su n tentativi indipendenti ognuno con probabilita' di successo assegnata p.
numero di sottozone, di una suddivisione di una area in n sottozone,
interessate ad un evento che ha probabilita' p di accadere in una sottozona indipendentemente dalle altre (faccio i tentativi in parallelo invece che uno dopo l'altro).
Media di una variabile aleatoria discreta.
(Varianza)
Convergenza della distribuzione binomiale per np= m (media) costante e n-->+oo.
Distribuzione di Poisson e sua interpretazione: gocce di pioggia e molto altro.
Definizione di variabile aleatoria reale con densita', definizione di media (varianza):
sostituire somme e serie con integrali.
********************************************************************
********************************************************************
I ciclo di ripetizione
.
12-1-09 ripetizione 1.I (Tortorelli) Esercizi sulle proprieta' algebriche di
potenze, esponenziali e logaritmi, e su monotonia di potenze, esponenziali e logaritmi.
Confronto tra numeri espressi con logaritmi e potenzecercando maggioranti o minoranti
per i quali si possono fare delle semplificazioni.
.
13-1-09 ripetizione 2.I (Tortorelli) Esercizi su propagazione degli errori nel prodotto e nella divisione, formula semplificata e formula approssimata dell'errore del prodotto.
Esercizi su moduli. Risoluzione di una diseguaglianza senza soluzioni esplicite. .
14-1-09 ripetizione 3.I (Tortorelli) Formula approssimata dell'errore del reciproco.
Serie geometrica e formula per differenza di potenze ennesime. Limiti notevoli per successioni e funzioni, tasso di interesse composto, limiti di frazioni di somme di infiniti, segmenti e rette come luoghi di zeri e come immagini di funzioni.
Esercizio sul polinomio di Taylor (da rifare la porssima volta).
15-1-09 ripetizione 4.I (Tortorelli) Sviluppi di Taylor di log cos x centro l'origine di grado 2 ed 8. Convergenza della serie di Taylor del coseno. Prodotti scalari, determinanti e funzioni trigonometriche. Piani con condizioni di ortogonalita' e in forma parametrica. Matrici e trasformazioni lineari. Matrici e cambiamenti di base. Distanza di piani da punti. Rotazioni nel piano attorno a punti arbitrari. Rotazioni nello spazio attorno ad un asse per l'origine.
16-1-09 ripetizione 5.I (Tortorelli) Volume tetraedro: sinteticamente e analiticamente, sottografici di rette e di piani, primitive di potenze. Principio di Cavalieri.
Volume cono di base data.
Esempio di estrazioni con ``rimbussolamento'' in confronto ad estrazioni senza ``rimbussolamento''. Distribuzione binomiale e schema di Bernoulli. Eventi
stocasticamente indipendenti. Come in certi casi di eventi dipendenti si possa calcolare la probabilita' di un'intersezione: esempio di applicazione formula di Bayes.
19-1-09 ripetizione 6.I (Tortorelli) Eventi indipendenti, valore atteso o media o speranza.
Ripetizione dell'esercizio probabilita' di estrarre esattamente 3 palline blu in 5 estrazioni da un urna con 2 verdi, 3 gialle e 5 blu.
Caso con ``rimbussolamento'' e caso senza ``rimbussolamento''.
Esercizio 1. Se PA|B=P B|A =1/2, e PA=1/4 dire quale delle seguienti affermazioni e' vera:
Ae B sono indipendenti
PB=PA
Esercizio 2. Un popolazione di H.W. presenta un carattere C nel caso di genotipo aa,
ove il gene presenta i due alleli A (dominante) e a (recessivo). Se la frequenza di a e' 0.2
calcolare.
- la probabilita' che un individuo nella popolazione non presenti C.
-la probabilita' che il figlio presenti C con madre che presenti Ce padre che non lo presenti.
-la probabilita' che almeno uno dei due genitori non presenti il carattere se il figlio lo presenta.
Esercizio 3. Estraendo ``con rimessa '' numeri da 1 a 90 calcolare il numero medio di estrazioni
per ottenere 5.
(impostazione: evento aleatorio N = numero di estrazioni per cui 5 compare solo nell'ultima
il numero medio di estrazioni perche' compaia 5 e' per definizione
somma su k di kP(N=k) = somma valore per probabilita' di assumere quel valore
Calcolo di P(N=k)= 1/90 (89/90)^{k-1}
quindi considerando che la serie
somme su h di (h+1) x^h e' la derivata della serie x somme su h di x^h = x/1-x
si deriva questa funzione si calcola la derivata in 89/90 e la simoltiplica per 1/90)
********************************************************************
********************************************************************
II ciclo di ripetizione
.
28-1-09 ripetizione 1.II (Tortorelli) Allineamenti decimali, prodotti notevoli, serie geometrica, assioma di Archimede, assioma di completezza per successioni, radici aritmetiche, esponenziale logaritmo, campi di definizione, pi-greco, costante e di Nepero e tasso di interesse composto, valore assoluto ed interpretazione geometrica dei numeri reali.
Esericizi crescita costante con decremento costante in percentuale, proprieta' esponenzili e logaritmi.
Errore relativo errore assoluto errore percentuale, valutazione prodotto.
.
29-1-09 ripetizione 2.II (Tortorelli) Esercizio su errore percentuale. Notazione insiemistica e regole formazione insiemi relazioni con le nozioni di base di logica. Concetto astratto di funzione. Grafici fondamentali e operazioni elementari sui grafici
.
2-2-09 ripetizione 3.II (Tortorelli) Coordinate cartesiane e distanze euclidee, grandezze trigonometriche, prodotto scalare ed interpretazione geometrica eproprieta' algebriche, determinate interpretazione geometrica e proprieta' algebriche.
Rette e piani in forma parametrica come immagine di cammini a velocita' costante, e come luoghi di zeri come condizioni di ortogonalita'. Equazione del piano passante per tre punti P, Q, R: det (X-P, Q-P, R-P)=0.
.
3-2-09 ripetizione 4.II (Tortorelli) Area di un parallelogramma nello spazio. Distanza tra un punto e un piano o una retta. Rapporto incrementale. Cambiamenti di base, prodotto righe per colonne, matrice inversa e matrice identica, formula per la matrice inversa, determinante del prodotto di due matrici quadrate. Trasformazioni lineari, associativita' del prodotto tra matrici, rotazioni e riflessioni nel piano. Matrici e sistemi.
.
4-2-09 ripetizione 4.II (Tortorelli) Calcolo differenziale ed integrale: dai rapporti incrementali e convessita' al polinomio di Taylor e al teorema fondamentale del calolo differenziale ed integrale. Esercizi e disegni.
.
5-2-09 ripetizione 4.II (Tortorelli) Moda, mediana, quantili, media esua proprieta' di minimo, varianza, punto di vista con ii pordotti scalari e diseguaglianza di Cauchy-Schwarz, covarianza, correlazione rette di regressione, ortogonalita' e non correlazione. Calcolo della numero medio di esami dati per studente sapendo il totale degli studenti e quanti studenti hanno dato ciascun esame: analisi del problema: la campionatura e' qui incognita si calcola la media ma non la varianza.
Spazi di probabilita' e regole di calcolo delle probabilita', probabilita' condizionata formule di Bayes e delle probabilita' totali. Esercizi. Media o valor atteso o speranza matematica di un numero aleatorio. Esercizi.
Eventi indipendenti: probabilita' di fare esattamente un 6 su 15 lanci di un dado non truccato. Schema di Bernoulli, distribuzione binomiale.
Numero delle funzioni da {1, ..., k} in {1, ..., n}, numero delle funzini iniettive (disposizioni con rimpiazzamento o senza),
cobinazioni e coefficienti binomiali.