http://WWW.dm.unipi.it/didactics/home.html
Elementi di Analisi Matematica II, Anno Accademico 2002-2003, Matematica
http://WWW.dm.unipi.it/didactics/home.html
![]() El. di An. Mat. I e II A.A. 2002/03
El. di An. Mat. I e II A.A. 2002/03
-------------------------------------------------------------
ESERCIZIO n. 1
a - Calcolare i seguenti limiti senza usare le funzioni esponenziali e logaritmiche, cercando di usare la definizione di limite, diseguaglianze e le principali proprietà dei limiti:
![]() ;
;
![]() ,
(si provi inoltre che è
decrescente);
,
(si provi inoltre che è
decrescente);
![]() ;
;
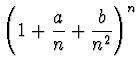 ,
,
![]() ;
;
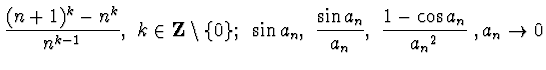
b - Calcolare gli stessi usando gli elementi di calcolo noti.
-------------------------------------------------------------
ESERCIZIO n. 2 Calcolare i limiti delle seguenti successioni
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
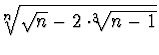 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
-------------------------------------------------------------
ESERCIZIO n. 3 Si provino le seguenti implicazioni, e si mostri che le implicazioni
inverse non sono vere.
a - bn >0,
![]()
![]() esponenzialmente.
esponenzialmente.
b - bn >0,
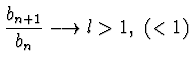
![]() esponenzialmente.
esponenzialmente.
c - an >0,
![]()
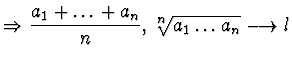 .
.
d - an >0,
![$\displaystyle{\frac {a_{n+1}}{a_n}\longrightarrow l\in [0 ;+\infty ]}$](img24.gif)
![]()
![]() .
.
e -
![]() ,
,
![]()
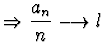 .
.
f * -
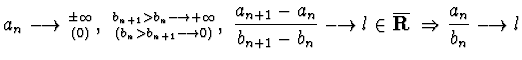 .
.
-------------------------------------------------------------
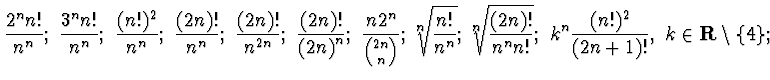
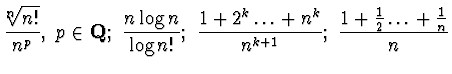
-------------------------------------------------------------
ESERCIZIO n. 5 Si provi che
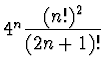 è decrescente
e che il suo estremo inferiore è non nullo.
è decrescente
e che il suo estremo inferiore è non nullo.
-------------------------------------------------------------
ESERCIZIO n. 6
a - Si provi per induzione
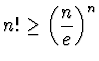 .
.
b - Utilizzando lo sviluppo di
Taylor per
![]() si provi che per ogni
si provi che per ogni
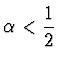 :
:
definitivamente
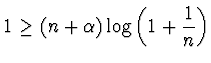 e
quindi definitivamente
e
quindi definitivamente
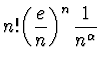 è crescente.
è crescente.
-------------------------------------------------------------
ESERCIZIO n. 7
Si calcoli il limite
![]() di
di
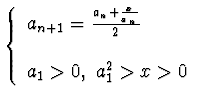 .
Si valuti l'infinitesimo
.
Si valuti l'infinitesimo
![]() .
.
Si provi che
![]() ove:
ove:
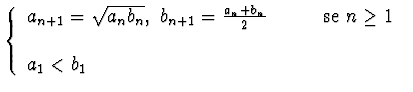
Si provi che la successione
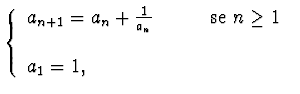 diverge. Si calcoli
diverge. Si calcoli
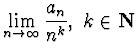
-------------------------------------------------------------
ESERCIZIO n. 8 * Studiare la convergenza della successione:
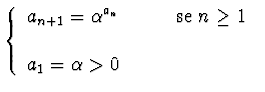
--------------------------------------- ---------------------
ESERCIZIO n. 9
a - Dato M>0, studiare la convergenza
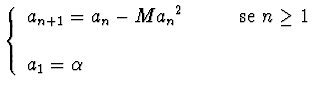
b * - Studiare la convergenza di
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 10 Si consideri la successione
![]() ,
,
![]() .
.
a - Si provi che non converge.
b * - Quali sono tutti i valori limite di sottosuccessioni della successione data?
-------------------------------------------------------------
ESERCIZIO n. 11 Una successione di numeri complessi
![]() ,
,
![]() converge ad un numero complesso
converge ad un numero complesso
![]() se e solo se:
se e solo se:
![]() ,
cioè se e solo se
,
cioè se e solo se
![]() .
Provare:
.
Provare:
a -
![]()
![]()
![]() e
e
![]()
![]()
![]() e
e
![]() .
.
b - se
![]() ,
,
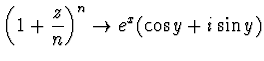 .
(Si
assuma che
.
(Si
assuma che
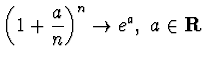 ).
).