http://WWW.dm.unipi.it/didactics/home.html
Elementi di Analisi Matematica II, Anno Accademico 2002-2003,
Matematica
http://WWW.dm.unipi.it/didactics/home.html
![]() El. di An. Mat. I e II A.A. 2002/03
El. di An. Mat. I e II A.A. 2002/03
-------------------------------------------------------------
ESERCIZIO n. 1 Risolvere o provare:
![]()
![]()
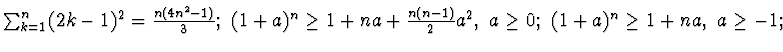
-------------------------------------------------------------
ESERCIZIO n. 2 Calcolare estremo superiore, inferiore, e specificare se sono
valori massimi o minimi dei seguenti sottoinsiemi di ![]() :
:
![$\displaystyle{ ]0;1],~[1;4[\cap (]0;2[\cup ]3;5]),~\bigcup_{n\in{\bf
N}}\left[ ...
...\bigcup_{m\in {\bf N}}\bigcap_{n\in{\bf
N}}\left]\frac 1{n+m} ; m+n\right[, ~ }$](img6.gif)
![]()
![]()
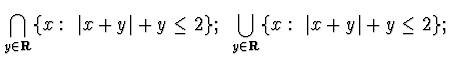
-------------------------------------------------------------
ESERCIZIO n. 3 Calcolare estremo superiore, inferiore, e specificare se sono
valori massimi o minimi delle seguenti funzioni e successioni a valori in
![]() :
:
![]()
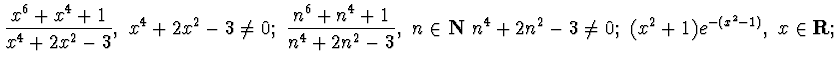
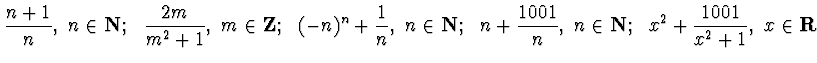
-------------------------------------------------------------
ESERCIZIO n. 4 Calcolare estremo superiore, inferiore, e specificare se sono
valori massimi o minimi delle seguenti funzioni e successioni a valori in
![]() :
:
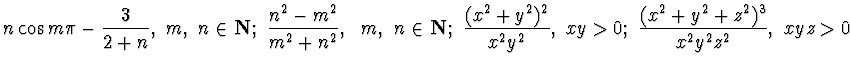
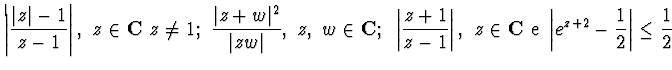
![]() , al variare di u
tra le funzioni per cui
, al variare di u
tra le funzioni per cui
![$\displaystyle{\sup\left\{ \left\vert \frac {du}{dx}(x)\right\vert ;x\in
[0;1]\right\}= 1}$](img16.gif)
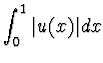 al variare di u tra
le funzioni per cui
al variare di u tra
le funzioni per cui
![]()
NOTAZIONE:
![]() ,
,
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 5 Provare che:
a - se
![]() allora
allora
![]() e
e
![]() ;
;
b -
![]() ,
,
![]() ,
,
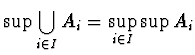 ;
;
c -
![]() ,
,
![]() ,
,
![]() ;
;
d - se
![]() ,
,
![]() allora:
allora:
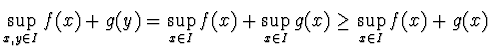 .
.
Si provi che la diseguaglianza è necessaria, e si trovi e provi un analogo enunciato per l'estremo inferiore;
-------------------------------------------------------------
ESERCIZIO n. 6
a - Se ![]() e
e
![]() allora x=0.
allora x=0.
b - Ogni sottogruppo additivo G di ![]() o è un sottoinsieme
denso o ha un minimo elemento positivo g0>0, e tale g0 genera G,
cioè
o è un sottoinsieme
denso o ha un minimo elemento positivo g0>0, e tale g0 genera G,
cioè
![]() .
.
c - Due numeri reali a, b hanno rapporto irrazionale se e solo se
![]() è un sottogruppo denso di
è un sottogruppo denso di ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 7 PRINCIPIO DI INDUZIONE Partendo dagli assiomi di ![]() ed da
quello dell'esistenza di intersezioni infinite si identifica l'insieme dei numeri
naturali come segue:
ed da
quello dell'esistenza di intersezioni infinite si identifica l'insieme dei numeri
naturali come segue:
![]() .
.
a - Si provi con questa definizione di ![]() che se
che se
![]() ,
,
![]() ,
,
![]() allora
allora ![]() .
.
b- Si dimostri che ogni sottoinsieme di ![]() ha minimo.
ha minimo.
-------------------------------------------------------------
ESERCIZIO n. 8
a -
Si provi che per ogni
![]() la funzione
la funzione
![]() ,
,
![]() è bigettiva da
è bigettiva da ![]() in se.
in se.
b - Detta
![]() la sua inversa che
la sua inversa che
![]() .
Il comune valore è indicato con
.
Il comune valore è indicato con
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 9 Dato
![]() e considerati
e considerati
![]() numeri reali non negativi si consideri la diseguaglianza:
numeri reali non negativi si consideri la diseguaglianza:
a - Si provi che se vale per n vale per 2n,
che se vale per n vale per tutti i suoi predecessori e
si concluda provando che è vera per ogni
![]() .
.
b - Fissato n per quali
![]() vi è eguaglianza.
vi è eguaglianza.
-------------------------------------------------------------
ESERCIZIO n. 10 Fissato
![]() ,
si
provi (eventualmente considerando i risultati dei due precedenti esercizi)
che la successione
,
si
provi (eventualmente considerando i risultati dei due precedenti esercizi)
che la successione
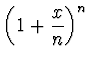 è crescente per
è crescente per ![]() ,
che
,
che
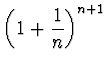 è decrescente, e quindi che la
prima è limitata superiormente.
è decrescente, e quindi che la
prima è limitata superiormente.