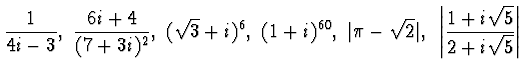
Elementi di Analisi Matematica II, Anno Accademico 2002-2003, Matematica

G. Albert, A. Briani, V.M. Tortorelli

I foglio di esercizi: V.M. Tortorelli

dal 20 febbraio 2003 al 25 febbraio 2003

Programma e materiale relativo ai corsi di Elemnti di Analisi Matematica I e II può essere reperito in rete selezionando nella Pagina del Dipartimento la voce Materiale Didattico (http://WWW.dm.unipi.it/didactics/home.html) e quindi selezionando Elementi di Analisi Matematica Uno e Due A.A. 2002/03.

-------------------------------------------------------------
ESERCIZIO n. 1 Calcolare :   $${\frac1{4i -3},~ \frac {6i+4}{(7+3i)^2 },~ (\sqrt{3}+i)^6 ,~(1+i)^... ...ert \pi - \sqrt{2}\vert,~ \left\vert\frac{1+i\sqrt{5}}{2+i\sqrt{5}}\right\vert}$$

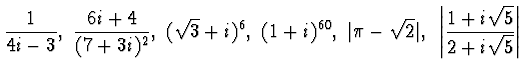
Scrivere in coordinate polari i numeri complessi $${2-i2,~ \sqrt{ 3}+i,~ \left(\frac{1+i}{1-i}\right)^3, (1-\sqrt{3})^{14}}$$

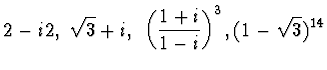
Calcolare :   $${\left((1+i)^n+(1-i)^n\right),~~ \left(\frac{1+i}{1-i}\right)^n }$$

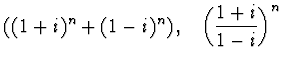
Dimostrare :   $${{\cal I}\! m z=\frac{z-\overline z}{2i},~ {\cal R}\! e z =\frac{z... ...{\overline z}{\vert z\vert^2},~ \vert z+w\vert \le \vert z\vert +\vert w\vert}$$

-------------------------------------------------------------
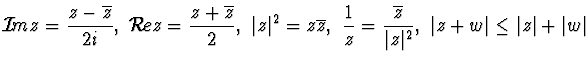
ESERCIZIO n. 2  Risolvere:

$z^5=\sqrt{3}-i,~~z^3 =8,~~ z^4+1=i\sqrt{3}, ~~ z^2+ 5z +8=0,~~z^2 +iz + i-3=0, ~{z^3-3iz^2-4z+2i=0,}~~$

${iz^3=\vert z\vert },~~ z^2+\vert z\vert +1=0,~~z^2+\overline{z}^2=\vert z\vert^2,~~ z^5+z^4+z^3+z^2+z+1=0$

Disegnare le regioni del piano complesso ripettivamente specificate dalle seguenti condizioni: $\vert z-1\vert\le 1-\vert z\vert,~\vert z-\overline{z}\vert\le \vert z+\overlin... ...\left\vert \frac{z-1}{z+1}\right\vert\le 1,~ \vert z\vert^4 =z^2+\overline{z}^2$

-------------------------------------------------------------
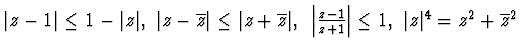
ESERCIZIO n. 3 Dimostrare che se $z_1\cdot \ldots z_n\not=0$ si ha:   $${\vert z_1 +\ldots z_n\vert =\vert z_1 \vert +\ldots \vert z_n \vert \Longleftrightarrow \frac{z_i}{z_j} >0}$$

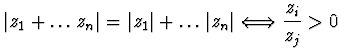
Se ne dia un'interpretazione geometrica.

-------------------------------------------------------------
ESERCIZIO n. 4 Si provi che il prodotto di somme di due quadrati di numeri interi è la somma di due quadrati di numeri interi.

-------------------------------------------------------------
ESERCIZIO n. 5

a- Dati v, z, $w\in {\bf C}$ si provi che l'area del triangolo che li ha come vertici è $\frac12 \left\vert{\cal I}\! m (w-v)\overline{(z-v)}\right\vert$

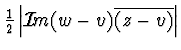
b- Dati due numeri complessi z e w si dia un'interpretazone geometrica a ${\cal R}\! e z\overline{w}$ e a ${\cal I}\! m z\overline{w}$.

-------------------------------------------------------------
ESERCIZIO n. 6 Le soluzioni di zⁿ =1 sono $e_{h+1}=e^{i2\pi \frac hn}$, $0\le h<n$. Per quali h si ha che $\{e_{h+1}, \ldots e_{h+1}^n\} =\{ e_1 ,\ldots e_n \}$?

-------------------------------------------------------------
ESERCIZIO n. 7

a- Si definisce $e^z = e^{{\cal R}\! e z}e^{i{\cal I}\! m z}$. Dato $z\in {\bf C}$ si trovino le soluzoni di w=e^z.

b- Si disegni la regione determinata da $\vert e^z -1\vert \le 1$ e la sua immagine tramite $z\mapsto e^z$.

-------------------------------------------------------------
ESERCIZIO n. 8

a- Si provi che un polinomio con coefficienti reali ha radici non reali complesse coniugate.

b- Si provi che ogni polinomio a coefficienti reali è prodotto di potenze di binomi di primo grado e di potenze di somme di numeri positivi con quadrati di binomi di primo grado.

c- Si trovi una primitiva di $\frac 1{t^4 +1}$ .

-------------------------------------------------------------
ESERCIZIO n. 9 Una funzione da ${\bf R}$ in ${\bf C}$ si dice derivabile se lo sono le sue componenti. In particolare e(t)=e^it lo è ed è l'unica soluzione di $e^\prime (t) =i e(t)$ per cui e(0)=1.

Se $z^2 +bz +c= (z-\mu) (z-\lambda )$, si provi che tutte e sole le soluzioni dell'equazione differenziale $u^{\prime\prime}(t) +bu^\prime (t) +c u(t) =(D^2 +bD +cI)u(t)=0$, sono del tipo $\alpha e^{i\mu t} +\beta e^{i\lambda t}$, o del tipo $\alpha e^{i\mu t} +\beta t e^{i\mu t}$, al variare di $\alpha$ e $\beta$ tra tutti i numeri complessi.

-------------------------------------------------------------
ESERCIZIO n. 10

a- Dati $\alpha$, $\beta\in {\bf C}$ e $\lambda \not= 1$ mostrare che $\vert z-\alpha \vert = \lambda \vert z-\beta\vert$ determina una circonferenza.

b- Cosa determina $\vert z-\alpha \vert= \vert z-\beta\vert$?

c- Le funzioni $z\mapsto \frac{\alpha z+\beta}{\gamma z+\delta}$ o sono costanti o trasformano cerchi e rette in cerchi o rette.

d- Trovare l'immagine del cerchio unitario e della bisettrice pricipale mediante l'applicazione

$z\mapsto \frac 12(z+z^{-1})$.

-------------------------------------------------------------
ESERCIZIO n. 11 a- Identificando ${\bf C}$ con ${\bf R}^2$ e dato $w\in {\bf C}$ l'associazione $z\mapsto w\cdot z$ definisce un'applicazione lineare da ${\bf R}^2$ in se. Si caratterizzino le matrici reali $2\times 2$ che corrispondono alla moltiplicazione per un numero complesso.

b- Da considerazioni elementari si ottiene che una trasformazione del piano in se che mantiene le distanze e ha tre punti fissi non allineati è l'identità.

c- Si provi che tutte e sole le trasformazioni del piano in se che mantengono le distanze e hanno l'origine fissa sono del tipo $z\mapsto w\cdot z$ o $z\mapsto w\cdot \overline{z}$, con $\vert w\vert=1$. In particolare sono lineari.