Complementi di Analisi Matematica

Anno Accademico 2003-2004

Laurea specialistica in Informatica

R.Stasi, V.M. Tortorelli

Soluzioni degli esercizi della I prova in itinere, 31 marzo 2004

-------------------------------------------------------------

1.a- Dire se esiste il limite $(x,y)\to (0,0)$ di $f(x,y)=\frac {\tan (x^2+y^2)}{\sqrt{ x^4 +y^4}}$.

$f(x,0)=\frac {\tan x^2}{x^2}\rightarrow 1$, $f(x,x)=\frac {\tan 2x^2}{x^2\sqrt{2}}\rightarrow \sqrt{2}$

R.: NO

1.b- Si calcoli il differenziale della funzione $\psi(x,y)= g(f(x,y))$ in $(1,1)$,

ove $f(x,y)= (xy, x^2-y^2)$, $g(u,v)= (\sin v, \cos u)$.

Derivando $g(f(x,y))= (\sin (x^2 -y^2), \cos xy )$ e calcolando in $(1,1)$ si ottiene $\psi^1_x = 2$, $\psi^1_y = -2$, $\psi^2_x = -\sin 1$, $\psi^2_y =-\sin 1$.

R.: $\left( \begin{array}{ll} 2 & -2\\ -\sin 1 & -\sin 1 \end{array}\right)$

1.c- Si calcoli il polinomio di Taylor del terzo ordine in 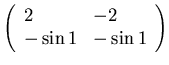$(0,0,0)$ della funzione $(\sin xyz , \cos xyz )$.

Dagli sviluppi in una variabile in $t=0$ $\sin xyz = {xyz}+ o(xyz)$, $\cos xyz= 1 + O(x^2y^2z^2)$. Ma $xyz= O(\vert (x,y,z)\vert^3 )$ per unicità del polinomio di Taylor:

R.: $( xyz , 1)$

2- Si calcolino i punti critici della funzione $f(x,y) = 2x^4-x^2 e^y +e^{4y}$ specificando se si tratta di punti di massimo o minimo relativo o meno.

Imponedo $f_x = 8x^3 -2x e^y=0$, $f_y =-x^2 e^y +4e^{4y}=0$ si ha $4x^2=e^y$ e $x^2 =4e^{3y}$. Quindi $e^y=1/4$, $x^2= 1/16$ e i punti ove si annulla il differenziale sono $(1/4, \log 1/4)$, $(-1/4, \log 1/4)$.

Inoltre $f_{xx}(\pm 1/4 , \log 1/4 )= 24 x^2 -2 e^y = 24/16 -2/4=1>0$, $f_{yy}(\pm 1/4 , \log 1/4 )= -1/16\cdot 1/4 +16/4>3$, $f_{xy}(\pm 1/4 , \log 1/4 )=f_{yx}= -2xe^y= \pm 1/2 \cdot 1/4=\pm 1/8$ per cui sia la traccia che il determinante della matrice Hessiana sono positivi

R.: $(1/4, \log 1/4)$, $(-1/4, \log 1/4)$, p.ti di minimo

3- Si calcoli $\frac{\partial z}{\partial x}_{\vert_{x=1,y=\sqrt{2}}}$ per la funzione definita implicitamente in un intorno di $(1,\sqrt{2}, 1)$ da

$f(x,y,z)=e^{x^2-y^2+z^2} -xz=0$.

Il punto $(1,\sqrt{2}, 1)$ verifica la condizione, $f_z (x,y,z)= 2ze^{x^2-y^2+z^2}-x$ non si annulla nel punto $(1,\sqrt{2}, 1)$ ove $f$ è nulla. Quindi $z=z(x,y)$ è ben definita e