 è sommabile in senso generalizzato si ha:
è sommabile in senso generalizzato si ha:
Concentrazione delle funzioni sommabili Se  è sommabile in senso generalizzato si ha:
è sommabile in senso generalizzato si ha:
 .
.
Per comodità di scrittura si consideri ![]() .
Per definizione
.
Per definizione
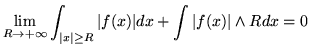 .
.
Se ![]() si ha
si ha
![]() che per
che per
![]() tende a
tende a
![]() .
.
Quindi
![]() .
.
Convergenza uniforme i- Limite uniforme di funzioni continue è continuo.
ii- Limite uniforme di funzioni Riemann integrabili su ![]() è Riemann integrabile su
è Riemann integrabile su ![]() .
.
iii- Se
![]() è uniformemente continua e
è uniformemente continua e ![]() , a valori in
, a valori in ![]() ,
converge uniformemente
ad
,
converge uniformemente
ad  su
su
![]() allora
allora ![]() converge uniformemente a
converge uniformemente a ![]() .
.
In particolare la somma di due successioni uniformemente convergenti è uniformemente convergente alla somma dei limiti.
iv- Se
![]() è solo continua e
è solo continua e ![]() converge uniformemente ad
converge uniformemente ad  limitata su
limitata su
![]() allora
allora ![]() converge uniformemente a
converge uniformemente a ![]() .
.
In particolare il prodotto di di due successioni uniformemente convergenti ed equilimitate è uniformemente convergente al prodotto dei limiti.
ii- Per il secondo asserto si tratta di provare che dato ![]() vi sono due suddivisoni per cui
vi sono due suddivisoni per cui
![]() è minore di
è minore di ![]() .
.
Si osserva che per ogni ![]() -rettangolo
-rettangolo ![]() contenuto in
contenuto in ![]()
![]() e
e
![]() sono minori di
sono minori di
![]() .
Quindi per due suddivisioni G e F si ha:
.
Quindi per due suddivisioni G e F si ha:
![]()
Fissato ![]() si considera
si considera ![]() per cui il primo addendo è minore di
per cui il primo addendo è minore di ![]() .
Per questo preciso
.
Per questo preciso ![]() vi sono due suddivisioni
vi sono due suddivisioni ![]() e
e ![]() per cui il secondo addendo
è anch'esso mionore di
per cui il secondo addendo
è anch'esso mionore di ![]() . Quindi fissato
. Quindi fissato ![]() per queste due suddivisioni
si ha quanto voluto.
per queste due suddivisioni
si ha quanto voluto.
iii- Per il terzo asserto fissato ![]() si considera
si considera ![]() per cui
per cui
![]() quando
quando
![]() . Come secondo passo si considera
. Come secondo passo si considera
![]() per cui se
per cui se
![]() è
è
![]() .
.
iv- Il quarto asserto segue osservando che se  è limitato tutte le
è limitato tutte le ![]() sono limitate
da eguali costanti indipendenti da
sono limitate
da eguali costanti indipendenti da ![]() . Ma allora le loro immagini son in un compatto e
. Ma allora le loro immagini son in un compatto e ![]() ristretta ad esso
è uniformemente continua.
ristretta ad esso
è uniformemente continua.
NOTA: in effetti una successione di funzioni che converge uniformemente è equilimitata se e solo se la funzione limite è limitata. Se invece la funzione limite non è limitata le funzioni della successione da un certo indice in poi non sono limitate.
Limiti di integrali. È immediato verificare che se
1- ![]() converge uniformemente ad
converge uniformemente ad  su
su ![]()
2- non solo le ![]() ma anche
ma anche  è sommabile su
è sommabile su ![]()
3- ![]() ha misura finita
ha misura finita
allora
![]() . Infatti:
. Infatti:
![]()
Continuità degli integrali dipendenti da parametro
Si consideri
![]() per cui:
per cui:
1-
![]() se
se ![]() ,
continuità in
,
continuità in ![]() uniforme rispetto a
uniforme rispetto a ![]() .
.
2- per ogni ![]() la funzione
la funzione
![]() è sommabile su
è sommabile su ![]()
3- ![]() ha misura finita
ha misura finita
allora
![]() è continua in
è continua in ![]() .
.
Per estendere il risultato a domini di misura non finita, se pur misurabili, si introduce la seguente nozione
Definizione: Una famiglia di funzioni sommabili
![]() si dice sommabile uniformemente (rispetto al parametro
si dice sommabile uniformemente (rispetto al parametro ![]() ) se:
) se:
![]() .
.
Ovvero gli integrali delle troncate convergono agli integrali uniformemente rispetto a
![]() .
.
- Famiglie ``equidominate''. Se per ogni ![]() e
e ![]() si ha
si ha
![]() per una stessa funzione sommabile
per una stessa funzione sommabile ![]() (che non dipende da
(che non dipende da ![]() !) allora la famiglia è sommabile uniformemente.
Tipiche funzioni di confronto sono le
!) allora la famiglia è sommabile uniformemente.
Tipiche funzioni di confronto sono le
![]() .
.
Proposizione: Se la successione ![]() è di funzioni sommabili uniformemente
rispetto ad
è di funzioni sommabili uniformemente
rispetto ad ![]() e converge uniformemente ad
e converge uniformemente ad  sui limitati allora
sui limitati allora  è sommabile e il suo integrale
è il limite degli integrali.
è sommabile e il suo integrale
è il limite degli integrali.
La sommabilità di  si deduce dalla R.-integrabilità delle
sue troncate e dal passaggio al limite per gli integrali delle troncate.
Quindi
si deduce dalla R.-integrabilità delle
sue troncate e dal passaggio al limite per gli integrali delle troncate.
Quindi
![]()
![]()
Fissato ![]() per concentrazione e sommabilità uniforme si trova
per concentrazione e sommabilità uniforme si trova ![]() per cui
il primo e l'ultimo addendo siano minori di
per cui
il primo e l'ultimo addendo siano minori di ![]() . Quindi per tale
. Quindi per tale ![]() si trova
si trova ![]() per cui se
per cui se
![]() il secondo addendo è minore anch'esso di
il secondo addendo è minore anch'esso di ![]() (passaggio al limite su domini di misura finita).
(passaggio al limite su domini di misura finita).
In conclusione fissato ![]() si è trovato
si è trovato ![]() t.c. se
t.c. se
![]()
![]()
Corollario Se
![]() è continua in
è continua in ![]() uniformemente rispetto a
uniformemente rispetto a ![]() , per ogni
, per ogni
![]() le
le
![]() sono sommabili,
e se
sono sommabili,
e se
![]() con
con ![]() sommabile su
sommabile su ![]() allora
allora ![]() è continua in
è continua in ![]() .
.
Vi sono i seguenti criteri di convergenza meno impegnativi (e relativi corollari per la continuità) :
Convergenza monotona se una successione crescente di funzioni sommabili non negative
Concentrazione delle funzioni sommabili Se  è sommabile in senso generalizzato si ha:
è sommabile in senso generalizzato si ha:
 .
.
Per comodità di scrittura si consideri ![]() .
Per definizione
.
Per definizione
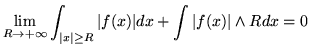 .
.
Se ![]() si ha
si ha
![]() che per
che per
![]() tende a
tende a
![]() .
.
Quindi
![]() .
.
Convergenza uniforme i- Limite uniforme di funzioni continue è continuo.
ii- Limite uniforme di funzioni Riemann integrabili su ![]() è Riemann integrabile su
è Riemann integrabile su ![]() .
.
iii- Se
![]() è uniformemente continua e
è uniformemente continua e ![]() , a valori in
, a valori in ![]() ,
converge uniformemente
ad
,
converge uniformemente
ad  su
su
![]() allora
allora ![]() converge uniformemente a
converge uniformemente a ![]() .
.
In particolare la somma di due successioni uniformemente convergenti è uniformemente convergente alla somma dei limiti.
iv- Se
![]() è solo continua e
è solo continua e ![]() converge uniformemente ad
converge uniformemente ad  limitata su
limitata su
![]() allora
allora ![]() converge uniformemente a
converge uniformemente a ![]() .
.
In particolare il prodotto di di due successioni uniformemente convergenti ed equilimitate è uniformemente convergente al prodotto dei limiti.
ii- Per il secondo asserto si tratta di provare che dato ![]() vi sono due suddivisoni per cui
vi sono due suddivisoni per cui
![]() è minore di
è minore di ![]() .
.
Si osserva che per ogni ![]() -rettangolo
-rettangolo ![]() contenuto in
contenuto in ![]()
![]() e
e
![]() sono minori di
sono minori di
![]() .
Quindi per due suddivisioni G e F si ha:
.
Quindi per due suddivisioni G e F si ha:
![]()
Fissato ![]() si considera
si considera ![]() per cui il primo addendo è minore di
per cui il primo addendo è minore di ![]() .
Per questo preciso
.
Per questo preciso ![]() vi sono due suddivisioni
vi sono due suddivisioni ![]() e
e ![]() per cui il secondo addendo
è anch'esso mionore di
per cui il secondo addendo
è anch'esso mionore di ![]() . Quindi fissato
. Quindi fissato ![]() per queste due suddivisioni
si ha quanto voluto.
per queste due suddivisioni
si ha quanto voluto.
iii- Per il terzo asserto fissato ![]() si considera
si considera ![]() per cui
per cui
![]() quando
quando
![]() . Come secondo passo si considera
. Come secondo passo si considera
![]() per cui se
per cui se
![]() è
è
![]() .
.
iv- Il quarto asserto segue osservando che se  è limitato tutte le
è limitato tutte le ![]() sono limitate
da eguali costanti indipendenti da
sono limitate
da eguali costanti indipendenti da ![]() . Ma allora le loro immagini son in un compatto e
. Ma allora le loro immagini son in un compatto e ![]() ristretta ad esso
è uniformemente continua.
ristretta ad esso
è uniformemente continua.
NOTA: in effetti una successione di funzioni che converge uniformemente è equilimitata se e solo se la funzione limite è limitata. Se invece la funzione limite non è limitata le funzioni della successione da un certo indice in poi non sono limitate.
Limiti di integrali. È immediato verificare che se
1- ![]() converge uniformemente ad
converge uniformemente ad  su
su ![]()
2- non solo le ![]() ma anche
ma anche  è sommabile su
è sommabile su ![]()
3- ![]() ha misura finita
ha misura finita
allora
![]() . Infatti:
. Infatti:
![]()
Continuità degli integrali dipendenti da parametro
Si consideri
![]() per cui:
per cui:
1-
![]() se
se ![]() ,
continuità in
,
continuità in ![]() uniforme rispetto a
uniforme rispetto a ![]() .
.
2- per ogni ![]() la funzione
la funzione
![]() è sommabile su
è sommabile su ![]()
3- ![]() ha misura finita
ha misura finita
allora
![]() è continua in
è continua in ![]() .
.
Per estendere il risultato a domini di misura non finita, se pur misurabili, si introduce la seguente nozione
Definizione: Una famiglia di funzioni sommabili
![]() si dice sommabile uniformemente (rispetto al parametro
si dice sommabile uniformemente (rispetto al parametro ![]() ) se:
) se:
![]() .
.
Ovvero gli integrali delle troncate convergono agli integrali uniformemente rispetto a
![]() .
.
- Famiglie ``equidominate''. Se per ogni ![]() e
e ![]() si ha
si ha
![]() per una stessa funzione sommabile
per una stessa funzione sommabile ![]() (che non dipende da
(che non dipende da ![]() !) allora la famiglia è sommabile uniformemente.
Tipiche funzioni di confronto sono le
!) allora la famiglia è sommabile uniformemente.
Tipiche funzioni di confronto sono le
![]() .
.
Proposizione: Se la successione ![]() è di funzioni sommabili uniformemente
rispetto ad
è di funzioni sommabili uniformemente
rispetto ad ![]() e converge uniformemente ad
e converge uniformemente ad  sui limitati allora
sui limitati allora  è sommabile e il suo integrale
è il limite degli integrali.
è sommabile e il suo integrale
è il limite degli integrali.
La sommabilità di  si deduce dalla R.-integrabilità delle
sue troncate e dal passaggio al limite per gli integrali delle troncate.
Quindi
si deduce dalla R.-integrabilità delle
sue troncate e dal passaggio al limite per gli integrali delle troncate.
Quindi
![]()
![]()
Fissato ![]() per concentrazione e sommabilità uniforme si trova
per concentrazione e sommabilità uniforme si trova ![]() per cui
il primo e l'ultimo addendo siano minori di
per cui
il primo e l'ultimo addendo siano minori di ![]() . Quindi per tale
. Quindi per tale ![]() si trova
si trova ![]() per cui se
per cui se
![]() il secondo addendo è minore anch'esso di
il secondo addendo è minore anch'esso di ![]() (passaggio al limite su domini di misura finita).
(passaggio al limite su domini di misura finita).
In conclusione fissato ![]() si è trovato
si è trovato ![]() t.c. se
t.c. se
![]()
![]()
Corollario Se
![]() è continua in
è continua in ![]() uniformemente rispetto a
uniformemente rispetto a ![]() , per ogni
, per ogni
![]() le
le
![]() sono sommabili,
e se
sono sommabili,
e se
![]() con
con ![]() sommabile su
sommabile su ![]() allora
allora ![]() è continua in
è continua in ![]() .
.
Vi sono i seguenti criteri di convergenza meno impegnativi (e relativi corollari per la continuità) :
Convergenza monotona se una successione crescente di funzioni sommabili converge semplicemente punto per punto ad una funzione anch'essa sommabile allora gli integrali convergono agli integrali del limite.
Questo criterio può essere dimostrato riducendosi a una successione crescente di funzioni, di una variabile, continue su un intervallo chiuso, e convergente ad una costante e quindi usando il seguente:
Lemma del Dini Se
1-
 sono funzioni continue su
sono funzioni continue su 
2- compatto
compatto
3-
![]() per ogni
per ogni ![]()
4-
![]() è continua su
è continua su 
allora la convergenza è uniforme.
Convergenza dominata se una successione equidominata di funzioni sommabili converge semplicemente punto per punto ad una funzione anch'essa sommabile allora gli integrali convergono agli integrali del limite.
La cornice teorica più adatta per provare tale teorema è quella dell'integrazione alla Lebesgue che estende la sommabilità generalizzata alla Riemann. In tale ambito più generale le ipotesi di sommabilità del limite risultano superflue.
Derivata di integrali. Un criterio per derivare un integrale dipendente da parametro si deduce da quanto detto:
sia
![]() per cui
per cui
![]() :
:
1-
![]() sono sommabile in
sono sommabile in ![]() per ogni
per ogni ![]()
2-
![]() uniformemente in
uniformemente in ![]()
3-
![]() sommabile in
sommabile in ![]() ,
,
si ha che
![]() è derivabile e
è derivabile e
![]() .
.
Infatti si scrive il rapporto incrementale di ![]() che è l'integrale del rapporto incrementale
di
che è l'integrale del rapporto incrementale
di
![]() che converge uniformemente a
che converge uniformemente a
![]() . D'altra parte tale
rapporto incrementale
per il teorema di Lagrange è
. D'altra parte tale
rapporto incrementale
per il teorema di Lagrange è
![]() . Ma indipendentemente da
. Ma indipendentemente da ![]() è dominato da una funzione sommabile. Si può quindi
passare al limite.
è dominato da una funzione sommabile. Si può quindi
passare al limite.
Corollario In particolare ciò avviene se
se
![]() : la condizione 2- segue da Lagrange e
dall'uniforme continuità della derivata, la condizione 3- dalla limitatezza della derivata che è continua su un compatto.
: la condizione 2- segue da Lagrange e
dall'uniforme continuità della derivata, la condizione 3- dalla limitatezza della derivata che è continua su un compatto.
Criterio di derivabilità conseguente al teorema di convergenza dominata
Utilizzando il criterio di convergenza dominata la pesante condizione sul limite uniforme può essere omessa e per ``scambiare derivata con integrale'' bastano le seguenti ipotesi:
la funzione è sommabile rispetto alla seconda variabile, la sua derivata rispetto alla prima variabile esiste sempre è non solo sommabile nella seconda variabile ma in modulo minore di una funzione sommabile ed indipendente dalla prima variabile.
la dimostrazione è identica alla precedente: il rapporto incrementale dell'integrale è l'integrale del rapporto incrementale rispetto alla prima variabile della funzione che tende alla derivata parziale. D'altra parte per Lagrange il rapporto è uguale alla derivata rispetto alla prima variabile in un valore intermedio del primo argomento e quindi è dominato indipendentemente dalla prima variabile dalla funzione che maggiora la derivata. Per convergenza dominata si conclude.
Continuità globale di
![]() con
con
![]()
Differenziabilità di
![]() con
con
![]() .
.
Derivata di
![]() , con
, con
![]() e
e
![]() ( limitate tra
( limitate tra ![]() e
e ![]() ):
):
![]()
Formula elementare di Gauss-Green nel piano per integrali non orientati in termini del vettore normale.
Sia ![]() un dominio normale regolare rispetto ad una delle direzioni coordinate. Per esempio
un dominio normale regolare rispetto ad una delle direzioni coordinate. Per esempio
![]() con
con
![]() differenziabili con continuità per cui il
bordo di
differenziabili con continuità per cui il
bordo di ![]() può essere parametrizzato come cammino regolare a tratti semplice e chiuso.
Tranne che nei quattro vertici risulta
può essere parametrizzato come cammino regolare a tratti semplice e chiuso.
Tranne che nei quattro vertici risulta ![]() il vettore unitario normale al bordo di
il vettore unitario normale al bordo di ![]() ed esterno a
ed esterno a
![]() (con seconda componente negativa sul grafico di
(con seconda componente negativa sul grafico di ![]() positiva su quello di
positiva su quello di ![]() ),
che risulta una funzione continua a tratti.
),
che risulta una funzione continua a tratti.
Con questa convenzione se ![]() sono funzioni differenziabili con continuità su
sono funzioni differenziabili con continuità su ![]() si ha
si ha

Estensione La stessa formula vale per domini che sono unioni di domini normali regolari rispetto ad una delle direzioni coordinate con parti interne disgiunte. In effetti gli integrali sui bordi comuni ai vari pezzi si cancellano essendo le normali esterne con direzioni opposte.
Derivabilità del limite di una successione di funzioni. Un criterio elementare è il seguente
I criterio Sia
![]() una successione di funzioni differenziabili con continuità su
una successione di funzioni differenziabili con continuità su ![$[a;b]$](img90.png) per cui:
per cui:
1-
![]() uniformemente su
uniformemente su ![$[a;b]$](img90.png)
2- per un certo ![]() la successioni di numeri
la successioni di numeri ![]() convergea un certo
convergea un certo ![]()
allora
3- la successione di funzioni ![]() converge uniformemente du
converge uniformemente du ![$[a;b]$](img90.png)
4- la funzione limite è derivabile e ha come limite ![]() .
.
La dimostrazione: per il teorema fondamentale del calcolo passando al limite sotto segno di integrale per
convergenza uniforme si ha la convergenza punto per punto delle ![]() :
:
![]()
Tale convergenza è uniforme:
![]()
![$\displaystyle{ \sup_{x\in [a;b]} \left\vert \int_{x_0}^x \vert f^\prime_n (t)-g...
...t)\vert +o(1)\le
(b-a) \sup_{t\in [a;b]}\vert f^\prime_n (t)-g (t)\vert +o(1)} $](img96.png)
Sempre per il teorema fondamentale il limite essendo una funzione integrale di ![]() , che è continua in quanto limite
uniforme di funzioni continue (le
, che è continua in quanto limite
uniforme di funzioni continue (le 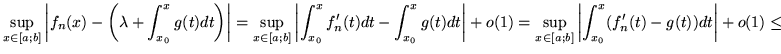 ), ha come derivata l'integranda.
), ha come derivata l'integranda.
Vale un enunciato più forte la cui dimostrazione richiede un minimo approfondimento delle proprietà della convergenza uniforme e si basa solo sul teorema di Lagrange (piuttosto che sul teorema fondamentale del calcolo e sulla continuità delle derivate):
II criterio Sia
![]() una successione di funzioni semplicemente differenziabili su
una successione di funzioni semplicemente differenziabili su ![$]a;b[$](img98.png) per cui:
per cui:
1-
![]() uniformemente sui sottointervalli chiusi di
uniformemente sui sottointervalli chiusi di ![$]a;b[$](img98.png)
2- per un certo ![]() la successioni di numeri
la successioni di numeri ![]() convergea un certo
convergea un certo ![]()
allora
3- la successione di funzioni ![]() converge uniformemente sui sottointervallli chiusi di
converge uniformemente sui sottointervallli chiusi di ![$]a;b[$](img98.png)
4- la funzione limite è derivabile e ha come limite ![]() .
.