-------------------------------------------------------------
Cammini. - Si dirà cammino una funzione continua
![]() , ove
, ove
![]() è un intervallo.
è un intervallo.
- Un cammino si dirà semplice se ![]() è iniettiva.
è iniettiva.
- Un cammino si dirà chiuso se ![]() è un intervallo chiuso
è un intervallo chiuso
![]() e
e
![]() (in altri termini corrisponde ad
una funzione continua dalla circonferenza unitaria in
(in altri termini corrisponde ad
una funzione continua dalla circonferenza unitaria in ![]() , ovvero una funzione
continua su
, ovvero una funzione
continua su ![]() che sia
che sia ![]() periodica).
periodica).
- Un cammino si dirà semplice chiuso se è chiuso ed è iniettivo tranne che negli estermi (la funzione che induce sulla circonferenza è iniettiva) .
- Un cammino si dirà ![]() se è differenziabile con continuità
se è differenziabile con continuità
![]() volte.
volte.
- Un cammino si dirà ![]() -
-![]() se è
se è ![]() e le sue prime
e le sue prime ![]() derivate sono cammini chiusi (ovvero induce una funzione su
derivate sono cammini chiusi (ovvero induce una funzione su ![]() che sia periodica
e
che sia periodica
e ![]() ).
).
- Un cammino si dirà regolare se è differenziabile e
![]()
- Un cammino si dirà ![]() , ovvero regolare, a tratti,
se
, ovvero regolare, a tratti,
se ![]() è unione di un numero finito di intervalli su ognuno dei quali
è unione di un numero finito di intervalli su ognuno dei quali
![]() è
è ![]() , rispettivamente regolare.
, rispettivamente regolare.
Parametrizzazioni. I cammini possono avere la stessa immagine ma rappresentare modi diversi
di ``percorrerla'': e.g.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
tutti hanno come immagine la circonferenza unitaria,
il primo la percorre una volta
con ``velocità '' in modulo costante eguale ad ![]() , il secondo
eguale a
, il secondo
eguale a ![]() , il terzo
la percorre due volte nello stesso senso, il quarto due volte in
senso differente.
, il terzo
la percorre due volte nello stesso senso, il quarto due volte in
senso differente.
- Volendo mettere in evidenza quante volte e in che verso
viene percorsa
l'immagine di un cammino piuttosto che ``quanto velocemente'' diremo
che due cammini
![]() e
e
![]() sono
equivalenti con la stessa orientazione
sono
equivalenti con la stessa orientazione
-------------------------------------------------------------
Cammini. - Si dirà cammino una funzione continua
![]() , ove
, ove
![]() è un intervallo.
è un intervallo.
- Un cammino si dirà semplice se ![]() è iniettiva.
è iniettiva.
- Un cammino si dirà chiuso se ![]() è un intervallo chiuso
è un intervallo chiuso
![]() e
e
![]() (in altri termini corrisponde ad
una funzione continua dalla circonferenza unitaria in
(in altri termini corrisponde ad
una funzione continua dalla circonferenza unitaria in ![]() , ovvero una funzione
continua su
, ovvero una funzione
continua su ![]() che sia
che sia ![]() periodica).
periodica).
- Un cammino si dirà semplice chiuso se è chiuso ed è iniettivo tranne che negli estermi (la funzione che induce sulla circonferenza è iniettiva) .
- Un cammino si dirà ![]() se è differenziabile con continuità
se è differenziabile con continuità
![]() volte.
volte.
- Un cammino si dirà ![]() -
-![]() se è
se è ![]() e le sue prime
e le sue prime ![]() derivate sono cammini chiusi (ovvero induce una funzione su
derivate sono cammini chiusi (ovvero induce una funzione su ![]() che sia periodica
e
che sia periodica
e ![]() ).
).
- Un cammino si dirà regolare se è differenziabile e
![]()
- Un cammino si dirà ![]() , ovvero regolare, a tratti,
se
, ovvero regolare, a tratti,
se ![]() è unione di un numero finito di intervalli su ognuno dei quali
è unione di un numero finito di intervalli su ognuno dei quali
![]() è
è ![]() , rispettivamente regolare.
, rispettivamente regolare.
Parametrizzazioni. I cammini possono avere la stessa immagine ma rappresentare modi diversi
di ``percorrerla'': e.g.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
tutti hanno come immagine la circonferenza unitaria,
il primo la percorre una volta
con ``velocità '' in modulo costante eguale ad ![]() , il secondo
eguale a
, il secondo
eguale a ![]() , il terzo
la percorre due volte nello stesso senso, il quarto due volte in
senso differente.
, il terzo
la percorre due volte nello stesso senso, il quarto due volte in
senso differente.
- Volendo mettere in evidenza quante volte e in che verso
viene percorsa
l'immagine di un cammino piuttosto che ``quanto velocemente'' diremo
che due cammini
![]() e
e
![]() sono
se
sono
se
![]() ,
, ![]() continua, invertibile crescente
e quindi con inversa continua
continua, invertibile crescente
e quindi con inversa continua
- Se non si `einteressati ai versi di percorrenza
si può introdurre una nozione di equivalenza meno stringente
ammettendo riparametrizzazioni ![]() continue e strettamente monotone.
continue e strettamente monotone.
NOTA: se un cammino ![]() a tratti è regolare
sulle parti interne di
un numero finito di intervalli che ricoprono
a tratti è regolare
sulle parti interne di
un numero finito di intervalli che ricoprono ![]() allora è equivalente
a un cammino
allora è equivalente
a un cammino ![]() -regolare a tratti
-regolare a tratti
Curve I cammini solo continui possono avere immagini
non aderenti all'idea intuitiva di curva: si possono trovare cammini
che ricoprono l'intero quadrato
![]() nel piano!
D'altronde un concetto geometrico che riguardi l'immagine di un cammino
se formalizzato in termini di cammini non deve dipendere da
parametrizzazioni equivalenti.
nel piano!
D'altronde un concetto geometrico che riguardi l'immagine di un cammino
se formalizzato in termini di cammini non deve dipendere da
parametrizzazioni equivalenti.
- Quindi in termini di cammini una curva orientata è la classe di equivalenza di cammini con un rappresentante regolare a tratti che tranne per un numero finito di parametri risulti iniettivo (che corrispondono ad un numero finito di ``autointersezioni'' dell'immagine).
Tangente Tranne un numero finito di punti un
insieme che può essere visto come immagine di una
parametrizzazione regolare a tratti del tipo precedente
ha una direzione tangente data dal versore tangente
![]() .
.
In particolare poichè
![]() dalla definizione di differenziabilità e per la diseguaglianza triangolare
si ha:
dalla definizione di differenziabilità e per la diseguaglianza triangolare
si ha:

ovvero l'errore dato dall'approssimazione lineare è infinitesimo relativamente a ciò che si desidera misurare.
![]() -superficie parametrica regolare - Si dice
-superficie parametrica regolare - Si dice ![]() -superficie
(parametrica) regolare una funzione
-superficie
(parametrica) regolare una funzione
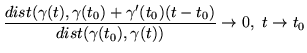 ove
ove
![]() è connesso, e
è connesso, e ![]() ,
per cui:
,
per cui:
i- la ![]() è restrizione di una funzione
è restrizione di una funzione ![]() su una perto
contenente
su una perto
contenente ![]()
ii- i vettori
![]() generano un sottospazio di dimenzione
generano un sottospazio di dimenzione ![]() in
in ![]() : ovvero vi siano
: ovvero vi siano
![]() indici
indici
![]()
per cui
![]()
- Una superficie parametrica si dirà semplice se è iniettiva.
NOTA: una
![]() che sia
che sia
![]() intorno alla chiusura di
intorno alla chiusura di ![]() da naturalmente una
da naturalmente una ![]() -superficie
che parametrizza il suo grafico
-superficie
che parametrizza il suo grafico
![]()
NOTA: il teorema del rango assicura che l'immagine di una superficie semplice è almeno localmente nel codominio un grafico.
- Come per le curve si ha che l'immagine di una
![]() -superficie ha in ogni suo punto
-superficie ha in ogni suo punto
![]() un piano tangente dato da
un piano tangente dato da
![]() al variare di
al variare di
![]() .
.
![]() -varietà I teoremi del Dini e del rango rendono
la seguente definizione naturale, in quanto non tutti i luoghi di zeri possono
essere visti come immagine di una superficie regolare semplice:
-varietà I teoremi del Dini e del rango rendono
la seguente definizione naturale, in quanto non tutti i luoghi di zeri possono
essere visti come immagine di una superficie regolare semplice:
- Un sottoinsieme ![]() di
di ![]() si dice
si dice ![]() -varietà se:
-varietà se:
per ogni ![]() vi è un intorno
vi è un intorno ![]() di
di ![]() e una
e una
![]()
i- ![]() e: o
e: o
![]()
ii- ![]() è
è ![]() ed iniettiva
ed iniettiva
iii- ![]() è
è ![]()
- La famiglia
![]() si dice sistema
di coordinate locali per
si dice sistema
di coordinate locali per ![]() , mentre le
, mentre le ![]() parametrizzazioni
locali.
parametrizzazioni
locali.
NOTA: ogni ![]() risulta una
risulta una ![]() -superficie parametrica semplice:
il suo differenziale ha rango massimo poichè composto con quello
di
-superficie parametrica semplice:
il suo differenziale ha rango massimo poichè composto con quello
di ![]() deve dare l'applicazione identica di
deve dare l'applicazione identica di ![]() .
.
Lunghezza - Si dice lunghezza di un cammino
![]()
- La lunghezza di un cammino è eguale per cammini equivalenti.
- Un cammino si dice rettificabile se ha lunghezza finita.
NOTA: intuitivamente la lunghezza defita non corrisponde alla misura dell'immagine ma alla misura del percorso fatto: ciò accade per cammini semplici.
Teorema Se
![$\gamma: [a;b] \to {\bf R}^n$](img57.png) è
è ![]() a tratti
a tratti
|
|
Integrazione non orientata di funzioni su superficie parametrica
Sulla falsariga del teorema di cambiamento di variabile negli integrali multipli,
considerando la corrispondenza tra somma dei determinanti minori ![]() di
di ![]() vettori in
vettori in ![]() e
e ![]() -volume del
-volume del ![]() -parellepipedo da essi generato
sembra naturale definire per una
-parellepipedo da essi generato
sembra naturale definire per una ![]() -superficie
-superficie ![]() il suo
il suo ![]() volume
come ``somma infinita'' dei
volume
come ``somma infinita'' dei ![]() -volumi dei parellelpipedi ``infinitesimi''
dati dall'approssimazione lineare
-volumi dei parellelpipedi ``infinitesimi''
dati dall'approssimazione lineare

NOTA: per una superficie semplice in effetti ciò corrisponde all'dea intuitiva di misura della sua immagine. Altrimenti tale nozione tiene conto delle diverse ``sovrapposizioni'' (su sottoinsiemi di misura non nulla del dominio) date dalla parametrizzazione.
- Data una funzione continua 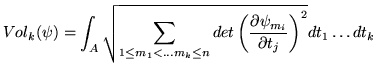 sull'immagine di una
sull'immagine di una
![]() -superficie
-superficie ![]() condominio misurabile si definisce
condominio misurabile si definisce
- Nel caso di ipersuperficie che sia un grafico
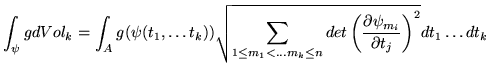 ovvero
ovvero ![]() e
e
![]() , si ottiene:
, si ottiene:
![]()
- Nel caso di cammini, per i quali la definizione si estende direttamente
nel caso ![]() a tratti, si ottiene:
a tratti, si ottiene:

Propopsizione
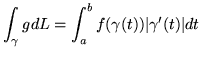 .
.
- Se
![]() è un cambiamento di variabile
regolare (con
è un cambiamento di variabile
regolare (con ![]() e
e ![]() misurabili e
misurabili e ![]() iniettiva con differenziale invertibile )
dal teorema di cambiamento di variabile per gli integrali multipli segue
che gli integrali rispetto a una superficie
iniettiva con differenziale invertibile )
dal teorema di cambiamento di variabile per gli integrali multipli segue
che gli integrali rispetto a una superficie
![]() su
su ![]() sono eguali a quelli
rispetto alla superficie
sono eguali a quelli
rispetto alla superficie
![]()
NOTA: in particolare l'integrazioni di funzioni su un cammino non dipendono dall'orientazione relativa di riparametrizzazioni.
- Nel caso di un insieme ![]() paramettrizzato da (che è immagine di ) una
paramettrizzato da (che è immagine di ) una ![]() -superficie semplice
ha senso scrivere
-superficie semplice
ha senso scrivere
![]()
Integrazione su varietà Per integrare una funzione su una varietà
si espime questa come unione di immagini di parametrizzazioni locali,
ovvero si scrive la funzione come somma di funzioni nulle fuori dagli intorni in
cui la varietà è immagine di una parametrizzazione locale, si integra su queste
e si somma.
Volumi e aree di figure di rotazione: formule di Guldino
Domini semplicemente connessi cfr. app. seconda parte lez. X.