 a tratti, definiti su
a tratti, definiti su
Lunghezza d'arco Richiamando le nozioni della sesta lezione
si introduce per cammini  a tratti, definiti su
a tratti, definiti su ![]() ,
la nozione di parametro di lunghezza d'arco che parametrizza in modo non arbitrario
l'immagine in funzione della lunghezza del percorso che si fa ``allontanandosi''
dal suo ``punto iniziale''
,
la nozione di parametro di lunghezza d'arco che parametrizza in modo non arbitrario
l'immagine in funzione della lunghezza del percorso che si fa ``allontanandosi''
dal suo ``punto iniziale''
il cammino
![]() per
cui
per
cui
![]() è equivalente a
è equivalente a ![]() e percorre la sua immagine
con ``velocità '' in modulo unitaria:
e percorre la sua immagine
con ``velocità '' in modulo unitaria:
![]() ma
ma
![]() .
.
Ciò è particolarmente significativo per quelle che si sono
chiamate curve orientate:
![]() da il versore
tangente.
da il versore
tangente.
Insiemi semplicemente connessi Si ricorda la nozione introdotta
nella sesta lezione che formalizza nel caso di sottoinsiemi del piano
la nozione intuitiva di ``non aver buchi''. Un sottoinsieme ![]() di
di ![]() si dice semplicemente connesso se è connesso (per archi)
e per ogni cammino
chiuso a valori in
si dice semplicemente connesso se è connesso (per archi)
e per ogni cammino
chiuso a valori in ![]() ,
,
![]() vi è
vi è
![]() ,
,
![]() ,
,
![]() ,
,
![]() è costante,
è costante,
![]() è un cammino chiuso
(
è un cammino chiuso
(
![]() )
)
intuitivamente: ![]() si deforma con continuità ad un punto
rimanendo in
si deforma con continuità ad un punto
rimanendo in
Lunghezza d'arco Richiamando le nozioni della sesta lezione
si introduce per cammini  a tratti, definiti su
a tratti, definiti su ![]() ,
la nozione di parametro di lunghezza d'arco che parametrizza in modo non arbitrario
l'immagine in funzione della lunghezza del percorso che si fa ``allontanandosi''
dal suo ``punto iniziale''
,
la nozione di parametro di lunghezza d'arco che parametrizza in modo non arbitrario
l'immagine in funzione della lunghezza del percorso che si fa ``allontanandosi''
dal suo ``punto iniziale''
il cammino
![]() per
cui
per
cui
![]() è equivalente a
è equivalente a ![]() e percorre la sua immagine
con ``velocità '' in modulo unitaria:
e percorre la sua immagine
con ``velocità '' in modulo unitaria:
![]() ma
ma
![]() .
.
Ciò è particolarmente significativo per quelle che si sono
chiamate curve orientate:
![]() da il versore
tangente.
da il versore
tangente.
Insiemi semplicemente connessi Si ricorda la nozione introdotta
nella sesta lezione che formalizza nel caso di sottoinsiemi del piano
la nozione intuitiva di ``non aver buchi''. Un sottoinsieme ![]() di
di ![]() si dice semplicemente connesso se è connesso (per archi)
e per ogni cammino
chiuso a valori in
si dice semplicemente connesso se è connesso (per archi)
e per ogni cammino
chiuso a valori in ![]() ,
,
![]() vi è
vi è
![]() ,
,
![]() ,
,
![]() ,
,
![]() è costante,
è costante,
![]() è un cammino chiuso
(
è un cammino chiuso
(
![]() )
)
intuitivamente: ![]() si deforma con continuità ad un punto
si deforma con continuità ad un punto
![]() .
.
Operazioni con cammini e curve - Dati due cammini ![]() su
su ![]() e
e ![]() su
su
![]() per cui
per cui
![]() si definisce il cammino giustapposizione o somma dei due
si definisce il cammino giustapposizione o somma dei due
![]() per
per ![]()
![]() per
per
![]()
- In maniera simile dato un cammino su ![]() si definisce il
cammino opposto
si definisce il
cammino opposto
![]()
Si ha
![]() , per cui
si scriverà
, per cui
si scriverà
![]() intendendo
intendendo
![]() qualora
sia definita.
qualora
sia definita.
- Queste operazioni sono compatibili con la relazione di equivalenza di cammini orientati: ovvero somme e opposti di cammini equivalenti sono equivalenti. Per questo motivo nella pratica spesso non conviene riparametrizzare il risultato su un unico intervallo ma mantenerlo definito a pezzi. Nella teoria queste operazioni si estendono a tali classi di equivalenza.
In particolare le classe dei cammini orientati chiusi (che iniziano da un prefissato punto) a valori in un dato insieme connesso per archi, con queste operazoni formano un gruppo (chiaramente non commutativo), che è indipendente dal punto di base prescelto (punti diversi sono collegati da un camino e dal suo opposto), chiamato gruppo dei lacci.
Omotopia di cammini con estremi fissati Due cammini
![]() e
e ![]() su
su ![]() a valori in
a valori in ![]() (connesso per archi),
per cui
(connesso per archi),
per cui
![]() e
e
![]() ,
ovvero hanno lo stesso punto iniziale e lo stesso punto finale,
si dicono omotopi in
,
ovvero hanno lo stesso punto iniziale e lo stesso punto finale,
si dicono omotopi in ![]() se esiste
se esiste
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() è un cammino con i prefissati estremi
(
è un cammino con i prefissati estremi
(
![]() )
)
- Questa nozione si estende di equivalenza di cammini orientati in quanto: cammini equivalenti a cammini omotopi sono omotopi, e inoltre due cammini possono essere riparametrizzati in modo lineare e crescente affinchè abbiano lo stesso dominio.
Si osserva che due cammini sono omotopi in ![]() se e solo se
il cammino chiuso
se e solo se
il cammino chiuso
![]() è omotopo in
è omotopo in ![]() ad un cammino costante.
In particolare un dominio
ad un cammino costante.
In particolare un dominio ![]() è semplicemente connesso
se e solo se cammini con gli stessi estremi sono omotopi in
è semplicemente connesso
se e solo se cammini con gli stessi estremi sono omotopi in ![]() .
.
- L'omotopia in ![]() risulta a sua volta una relazione di equivalenza
tra (classi di equivalenza di ) cammini orientati a valori in
risulta a sua volta una relazione di equivalenza
tra (classi di equivalenza di ) cammini orientati a valori in ![]() .
Inoltre giustapposizione e opposto di cammini omotopi sono omotopi al risultato
rispettivo delle operazioni.
.
Inoltre giustapposizione e opposto di cammini omotopi sono omotopi al risultato
rispettivo delle operazioni.
- Ne segue che in un dominio ![]() connesso per archi
l'equivalenza data dall'omotopia proietta il gruppo dei lacci su un gruppo
relativamente più semplice daa studiare chiamato primo gruppo di omotopia
dello spazio
connesso per archi
l'equivalenza data dall'omotopia proietta il gruppo dei lacci su un gruppo
relativamente più semplice daa studiare chiamato primo gruppo di omotopia
dello spazio ![]() in questione ed è uno strumento algebrico per studiare proprietà
geometriche di
in questione ed è uno strumento algebrico per studiare proprietà
geometriche di ![]() (e.g. un dominio semplicemente connesso ha primo gruppo di omotopia
di un solo elemento, se un dominio piano ha primo gruppo di omotopia isomorfo
ai numeri interi ha esattamente un ``buco'' etc.).
(e.g. un dominio semplicemente connesso ha primo gruppo di omotopia
di un solo elemento, se un dominio piano ha primo gruppo di omotopia isomorfo
ai numeri interi ha esattamente un ``buco'' etc.).
Integrazione orientata di campi ed ![]() -forme: lavoro Un concetto
fondamentale in fisica
è quello di lavoro di una forza lungo un cammino:
l'idea intuitiva di ``somma infinita'' del prodotto tra
la componente tangenziale di una forza applicata in un punto
-forme: lavoro Un concetto
fondamentale in fisica
è quello di lavoro di una forza lungo un cammino:
l'idea intuitiva di ``somma infinita'' del prodotto tra
la componente tangenziale di una forza applicata in un punto ![]() per lo spostamento ``infinitesimo'' lungo la traiettoria
per lo spostamento ``infinitesimo'' lungo la traiettoria
![]() nello stesso punto.
nello stesso punto.
Da un punto di vista matematico avanzato lo studio di proprietà geometriche tramite il gruppo dei lacci risultano spesso impegnative: estensioni del concetto di ``lavoro lungo una curva'' sono la base per studiare proprietà geometriche meno impegnative ma decisamente più maneggevoli da analizzare.
- Su ![]() in
prima istanza un campo vettoriale (vettori applicati in punti) su
in
prima istanza un campo vettoriale (vettori applicati in punti) su
![]() è indotto
da una funzione
è indotto
da una funzione
![]() continua.
continua.
- Un cammino ![]() in
in ![]() definisce in ogni punto
definisce in ogni punto
![]() della sua immagine un vettore tangente
della sua immagine un vettore tangente
![]() . Un cammino
differenziabile con continutà individua un campo di vettori sulla sua
immagine.
. Un cammino
differenziabile con continutà individua un campo di vettori sulla sua
immagine.
PROBLEMA: se in un aperto di ![]() di
di ![]() è definito un campo
esiste una famiglia di curve che ricopre l'aperto e ognuna di esse
ha come tangente il campo stesso?
è definito un campo
esiste una famiglia di curve che ricopre l'aperto e ognuna di esse
ha come tangente il campo stesso?
- Se ![]() è un campo su
è un campo su ![]() ,
, ![]() un cammino
un cammino  a tratti
a valori in
a tratti
a valori in ![]() e definito su
e definito su ![]() ,
si dice lavoro di
,
si dice lavoro di ![]() su
su ![]() :
:
NOTA: a ![]() si
può rimpiazzare il campo tangente a
si
può rimpiazzare il campo tangente a ![]() otteneuto dalla proiezione ortogonale di
otteneuto dalla proiezione ortogonale di 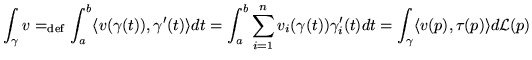 su
su ![]() .
.
- Tenendo presente che le coordinate cartesiane
permettono di identificare punti, vettori e funzionali lineari
concettualmente diversa è la nozione di ![]() -forma differenziale
su
-forma differenziale
su ![]() che in prima istanza viene individuta da una funzione continua
che in prima istanza viene individuta da una funzione continua ![]() da
da ![]() in
in ![]() :
:
![]() . In tale contesto è comodo
denotare
. In tale contesto è comodo
denotare ![]() con
con ![]() .
.
Analogamente si definisce l'integrale
(il lavoro) di una ![]() -forma
-forma ![]() su
su ![]() lungo un a cammino in
lungo un a cammino in ![]() come l'integrale
rispetto la lunghezza d'arco della funzione ottenuta applicando la forma nel punto al vettore unitario
tangente alla curva nel punto
come l'integrale
rispetto la lunghezza d'arco della funzione ottenuta applicando la forma nel punto al vettore unitario
tangente alla curva nel punto
Se si vuole identificando i vettori con spostamenti o velocità, in assenza di di sistemi di riferimento una forza non può che essere un funzionale lineare.
NOTA: l'integrazione di campi o forme lungo cammini si differenzia da quella di funzioni in quanto non è invariante rispetto all'inversione del cammino:
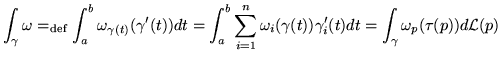
mentre, come per l'integrale di funzioni, per l'integrale di forme vale
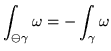
- Tipici esempi di campo vettoriale e di ![]() - forma differenziale
sono il gradiente e la funzione differenziale di una funzione
- forma differenziale
sono il gradiente e la funzione differenziale di una funzione  su un aperto
su un aperto
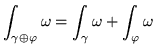
- La ![]() -forma differenziale costantemente eguale alla
-forma differenziale costantemente eguale alla ![]() proiezione coordinata
proiezione coordinata
![]() , i.e.
, i.e.
![]() , viene indicata con
, viene indicata con ![]() :
e questo è coerente
con il fatto che l'applicazione lineare
:
e questo è coerente
con il fatto che l'applicazione lineare ![]() ha come differenziale in ogni punto se stessa.
ha come differenziale in ogni punto se stessa.
Le ![]() -funzioni che identificano una froma differenziale
-funzioni che identificano una froma differenziale
![]() non sono altro che i coefficienti della forma
espressa come combinazione dei differenziali delle coordinate:
non sono altro che i coefficienti della forma
espressa come combinazione dei differenziali delle coordinate:
- D'altra parte fissato
![]() e un vettore
e un vettore ![]() (un campo su un punto)
per ogni funzione regolare in un intorno di
(un campo su un punto)
per ogni funzione regolare in un intorno di ![]() è definita
è definita
![]() . Quindi (indicata con
. Quindi (indicata con ![]() la funzione di valutazione in
la funzione di valutazione in ![]() :
:
![]() ) un campo si identifica
con ``un'operatore di derivazione'' puntulale, e i campi che danno in ogni
punto i vettori coordinati con i rispettivi operatori di derivazione parziale
nel punto:
) un campo si identifica
con ``un'operatore di derivazione'' puntulale, e i campi che danno in ogni
punto i vettori coordinati con i rispettivi operatori di derivazione parziale
nel punto:
Differenza tra funzioni e campi o forme. È bene osservare
che sebbene a livello introduttivo si siano presentati i campi e le forme
proprio come ![]() -ple di funzioni i concetti sottointesi sono molto diversi:
quando con le
-ple di funzioni i concetti sottointesi sono molto diversi:
quando con le ![]() -funzioni si intende un campo o una forma differenziale si considera
una diversa legge di cambiamento di questa rapprasentazione quando cambino
in maniera generale le coordinate del dominio.
-funzioni si intende un campo o una forma differenziale si considera
una diversa legge di cambiamento di questa rapprasentazione quando cambino
in maniera generale le coordinate del dominio.
La situazione è analoga a quella di un ![]() -pla di numeri
che rappresenta sia un vettore che un funzionale lineare: la differente denotazione
si caratterizza nel diverso modo in cui cambia la
-pla di numeri
che rappresenta sia un vettore che un funzionale lineare: la differente denotazione
si caratterizza nel diverso modo in cui cambia la ![]() -pla cambiando semplicemente
in modo lineare le coordinate.
1
-pla cambiando semplicemente
in modo lineare le coordinate.
1
- Nel caso in questione, invece di semplici cambiamenti di
coordinate lineari, si
considerano cambiamenti di coordinate  : si considera un
: si considera un ![]() aperto di
aperto di ![]() e una sua ``riparametrizzazione''
e una sua ``riparametrizzazione''
![]() una funzione
una funzione  bigettiva con inversa
bigettiva con inversa  , le nuove funzioni coordinate saranno appunto date
, le nuove funzioni coordinate saranno appunto date
![]() .
.
Questo sistema di coordinate da in ogni punto di ![]() una diversa
base di vettori dello ``spazio tangente'' in
una diversa
base di vettori dello ``spazio tangente'' in ![]() che nel caso è
che nel caso è ![]() .
Per maggior chiarezza si indichi la
.
Per maggior chiarezza si indichi la ![]() -pla di
-pla di ![]() composta da zeri tranne che
un
composta da zeri tranne che
un ![]() all'
all' posto con
posto con ![]() se si pensa come vettore applicato in un
punto di
se si pensa come vettore applicato in un
punto di ![]() e con
e con ![]() se si pensa come vettore applicato in un punto
se si pensa come vettore applicato in un punto ![]() .
.
Nelle coordinate rispetto
![]() la nuova base è
la nuova base è
 ,
che corrispondono alle ``velocità '' delle curve immagine mediante
,
che corrispondono alle ``velocità '' delle curve immagine mediante ![]() delle direzioni coordinate cartesiane in
delle direzioni coordinate cartesiane in ![]() parametrizzate linearmente:
parametrizzate linearmente:
![]() .
.
- Una ![]() -pla di funzioni
-pla di funzioni ![]() definite in
definite in ![]() se considerata come
funzione si trasforma semplicemente in
se considerata come
funzione si trasforma semplicemente in
![]() .
Quando si considera la
.
Quando si considera la
![]() -pla di funzioni come forma differenziale la trasformazione
`` diretta'' per la regola della catena sui differenziali
-pla di funzioni come forma differenziale la trasformazione
`` diretta'' per la regola della catena sui differenziali
![]() è
è
in effetti come funzione lineare che agisce sulle nuove coordinate
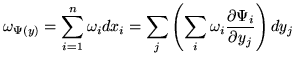 si ottine semplicemente:
si ottine semplicemente:
quindi alla ![]() -pla
-pla
![]() corrisponde
la
corrisponde
la ![]() -pla
-pla
![]()
- Nel caso in cui la forma è il differenziale di una funzione ![]() da
da ![]() in
in ![]() si ha in effetti per l a regola della catena
si ha in effetti per l a regola della catena
![]() . Quindi il differenziale
rispetto alle nuove variabili è proprio l'esperssione della forma nelle nuove
variabili.
. Quindi il differenziale
rispetto alle nuove variabili è proprio l'esperssione della forma nelle nuove
variabili.
-
Se si considera invece una ![]() -pla come
campo di vettori e si vogliono le sue coordinate
rispetto alla base indicata si ottengo le
-pla come
campo di vettori e si vogliono le sue coordinate
rispetto alla base indicata si ottengo le ![]() -funzioni
-funzioni
![]() : ovvero le coordinate
di
: ovvero le coordinate
di ![]() rispetto al riferimento cartesiano
rispetto al riferimento cartesiano
![]() di
di ![]() : se
: se
![]() applicando
applicando ![]() si ottiene
si ottiene
![]() .
.
- La nozione di campo come derivazione giustifica
la richiesta di questa trasformazione:
se si considera la derivazone definita da ![]() rispetto
alle variabili
rispetto
alle variabili ![]() essa espressa come derivazione
rispetto alle variabili
essa espressa come derivazione
rispetto alle variabili ![]() , avendo per la regola della catena
, avendo per la regola della catena
![]()
da luogo ad una diversa ![]() -pla di funzioni:
-pla di funzioni:
![]()
- Ancor di più si apprezza questa differenza considerando il caso
in cui ![]() è una
è una ![]() -superficie regolare parametrizzata da qualche
-superficie regolare parametrizzata da qualche
![]() e la funzione
e la funzione ![]() dia un vettore
tangente nel punto in cui la si calcola. In questo caso la base dello spazio
tangente in
dia un vettore
tangente nel punto in cui la si calcola. In questo caso la base dello spazio
tangente in ![]() disponibile è
disponibile è
![]() .
.
Un cambiamento di coordinate su ![]() :
: ![]() da
una riparametrizzazione di
da
una riparametrizzazione di ![]() ,
,
![]() , e quindi
una nuova base del tangente in ogni punto.
, e quindi
una nuova base del tangente in ogni punto.
- Nel caso in cui il campo sia una gradiente
![]() con
con
![]() la sua espressione nelle nuove coordinate
la sua espressione nelle nuove coordinate
![]() non è il gradiente rispetto
ad esse della
non è il gradiente rispetto
ad esse della
![]() .
.
![]()
Rimontato (pull-back)di una forma
Più in generale se
![]() è una mappa
è una mappa  ed
ed ![]() una forma differenziale su
una forma differenziale su ![]() si definisce la forma differenziale rimontata (pull-back)
di
si definisce la forma differenziale rimontata (pull-back)
di ![]() mediante
mediante
![]() su
su ![]() come
come
![]() . Essa viene denotata
con
. Essa viene denotata
con
![]() .
.
- Se ![]() è una funzione definita su
è una funzione definita su ![]() si indicherà
ancora con
si indicherà
ancora con
![]() la funzione composta
la funzione composta
![]() . Chiaramente per la regola della catena:
. Chiaramente per la regola della catena:
- Se ![]() è una funzione a valori in
è una funzione a valori in ![]() si indicherà
con
si indicherà
con
![]() la sua immagine
la sua immagine
![]() .
.
- Infine tale trasformazione è esattamente quello che ci aspetta dall' ``azione'' delle funzioni vettoriali sui cammini: il lavoro non deve cambiare cambiando sistema di coordinate
I principali teoremi: caratterizzazione forme esatte e campi conservativi, forme chiuse e forme localmente esatte, Teorema di Poincarè , invarianza per omotopia regolare dell'integrale di una forma chiusa o localmente esatta, esattezza delle forme e integrabilità di campi chiusi su domini semplicemente connessi. Cfr. C.J e F.M.S.
Formula di Gauss-Green mediante integrazione orientata
![]() -forma dell'area
-forma dell'area