Presentazione del corso e dei docenti :
breve commento sui prerequisiti auspicabili al corso e sugli obiettivi formativi da raggiungere.
(Per qualche esercizio
- oltre a quelli distribuiti per le prove di ammissione e di verifica vedere,
- quelli relativi agli argomenti prerequisiti accennati nei testi consigliati o altri testi di vostro gradimento,
(per esampio [VV] cap. 4 pagg. 55-69),
-tra quelli a cura del Dottor Jmmy Mauro per il corso dello scorso anno i seguenti:
esercitazione I sistemi di disequazioni di razionali, equazioni e disequazioni per trinomi in una variabile,
esercitazione III la seconda parte da pag. 3 in poi, disequazioni irrazionali e logaritmiche,
esercitazione IV-1 diseguaglianze per determinare ove hanno senso alcune espressioni,
esercitazione VI-3
-le prime domande dei testi di esame dello scorso anno ,
-tra quelli del materiale didattico nel sito del corso dello scorso anno della Prof.ssa P.Cerrai,
-tra quelli del materiale didattico nell'archivio didattico del Prof. G.Alberti, in particolare quello dello scorso anno e tra le esercitazioni a cura di V.M.Tortorelli allo stesso corso
esercitazione II
esercitazione III )
Riferimenti (per la lezione in oggetto):[EB] cap. 1 pagg. 1-10 pagg. 13-14, [MA1] cap. 1 pagg. 1-10, [BDM] cap. 1 pagg. 23-25.
1- Confronto : minore e ``minore o uguale'', le regole degli ordinamenti totali (cenno alle scale nominali, ordinali e rapportali)
(piu grande in senso stretto: >)
a non e' piu' grande di a
se a e' piu' grande di b e be' piu' grande di c allora a e' piu' grande di c
dati a e b si ha che o a e' eguale a b, o a e' piu' grande di b, o b e' piu' grande di a
- Il confronto di numerosita' e l'astrazione del concetto di numero: rappresentazioni simboliche e posizionali in data base.
-Il sistema dei numeri naturali: le regole della somma e del prodotto, 0,1, le regole della somma e del prodotto e l'ordinamento dei numeri naturali (si ricordi che 3 e' maggiore o eguale a 3).
-La regola teorica del principio di induzione:
ogni famiglia di numeri naturali, che abbia almeno qualche elemento, ha un suo elemento che e' piu' piccolo di tutti gl altri elementi della famiglia.
Un asserto equivalente e' :
data una proprieta' P
se 0 verifica P
e
se dal fatto che un numero naturale x verifica P si riesce a dedurre che x+1 verifica P
(la proprieta' passa al successore)
allora
ogni numero naturale verifica P
(Che siano asserti equivalenti si puo vedere per esempio come segue [argomento non svolto lezione]:
se F e' una famiglia di numeri che in effetti ha qualche numero come suo elemento si considera la proprieta' P di ``non essere membro della famiglia insieme ai numeri che lo precedono''. Se F non avesse l'elemento piu' piccolo allora: in particolare 0 verificherebbe P, ed inoltre se x fosse un numero che verifica P, cioe' che non sta nella famiglia insieme ai suoi predecessori, anche x+1 verificherebbe P . Ma allora tutti i numeri la verificherebbero
cioe' non starebbero in F, che pero' dovrebbe avere qualche numero e quindi l'assunzione
che F non abbia un numero piu' piccolo e' in contraddizione con l'assunzione che abbia almeno un numero.
Viceversa data la proprieta' P valida per 0 e che `passa al successore' se non fosse valida per tutti i numeri la famiglia F dei numeri che non soddisfano P avrebbe qualche numero: se x e' il suo numero piu' piccolo sara' diverso da 0, quindi x=y+1 per qualche numero y che non puo' stare in F, in quanto piu' piccolo di x, cioe' y verifica P. Ma allora anche y+1=x verificherebbe P cioe' x non sarebbe in F pur essendo il piu' piccolo dei numeri di F.)
Questa proprieta' astratta piu' che essere applicata e' ispirata dalla pratica di ragionamenti e calcoli elementari. E' lo strumento teorico per dimostrare asserti su quantita' Q(x) dipendenti da un numero naturale x che si calcolino con x e i suoi predecessori e Q(x-1) , ... , Q(0).
-Esemplificazione (vedi esercizi svolti) e definizione di fattoriale e suo significato
n! il prodotto dei primi n numeri naturali diversi da 0 (se n e' diverso da 0)
0! per convenzione e' 1.
usando solo i termini dei numeri si definisce la quantita' in questione ``per ricorrenza''
(n+1)!= (n+1) x n!
0! = 1
NOTA: l'uso dei puntini nelle due situazioni seguenti
n! =1x 2x ... x n
`` consideriamo i numeri 2 ... 14''
e' sostanzialmente diverso la prima e' una suggestiva notazione della definizione di fattoriale sopra data, la seconda una semplice abbreviazione.
-Il simbolo e la definizione di sommatoria e di `produttoria'
data una successione di numeri a(1), a(2), ... a(n) ...
S(N+1)= S(N) + a(N+1)
S(1)= a(1)
S(N)= a(1)+ ...+a(N)
P(N+1)= P(N)x a(N+1)
P(N)= P(1)x...xP(N)
1-10-09 esercitazione 1 (Tortorelli 30 min.) Esercizi ed esempi svolti: situazione artificiale in cui confrontando tre corpi X, Y, Z con una bilancia bracci se X>Y, Y>Z, si ha Z>X,
scrivere i primi dieci numeri in base 2,
scrivere 37 in base 12,
somme `in colonna' in base 2,
in quanti modi M(5) con 5 etichette diverse si etichettano 5 barattoli diversi
(il principio di induzione in pratica: ho cinque possibilta'
per etichettare uno in particolare dei barattoli, per ognuna di queste 5 scelte ho da calcolare in quanti modi si etichettano 4 barattorli con 4 etichette, ne prendo un'altro ho 4 possibilita', e per ognuna di queste ho da calcolare in quanti modi si etichettano 3 barttoli con tre etichette ... M(5)=5 x M(4)= 5 x 4 x M(3)= ...=5x4x3x2x1=120),
anagrammi della parola `sei'.
- Esercizi lasciati: in quanti modi si scambiano le magliette 42 studenti?
quanti sono gli anagrammi della parola `sette'?
5-10-09 lezione 2 ( ore 1 e 30 min.)
Riferimenti (per la lezione in oggetto): [EB] cap. 1 pagg. 12 pagg. 15-20, cap. 81 pagg. 202-203, cap. 13.7 pagg. 423-431, [MA1] cap. 2.4 pagg. 58-59 cap. 2.9 pagg. 81-91, [BDM] cap. 1 pagg. 25-39 , [VV] cap 11 pagg. 239-240 cap 11.5 pagg 269-271.
Disposizioni (estrazioni) semplici e con ripetizione, combinazioni, fattore binomiale e formula di ricorrenza con il metodo del testimone, formula di Newton per la potenza di un binomio,
multinomiali ed anagrammi, formula per la potenza di un ``multinomio''.
Significato combinatorico di somma e prodotto.
Numeri interi (relativi).
Numeri primi e divisibilita'.
Teorema di fattorizzazione unica (commento sulla potenza di codifica dei numeri naturali).
Teorema di divisibilita' tra numeri interi.
Commensurabilta' di grandezze frazioni, rapporti e numeri razionali:
- criterio di commensurabilita' di segmenti: due segmenti sono commensurabili (vi e' un eventuale terzo segmento che ripetuto ricopre esattamente oognuno dei due) se e soltanto se riportando il piu' corto sul piu' lungo e fermandosi il passo prima di ricoprire quest'ultimo e ripetendo la procedura con il resto al posto del segmento piu' corto e questi al posto del piu' lungo il proceesso ha termine;
- la grandezza lineare della diagonale del quadrato non e' commensurabile con quella del lato: provando a riportare il lato sulla diagonale e continuando a cercare di ricoprire con il resto il resto precedente si ottiene una ``costruzione geometrica che non termina'' perche' in due passi ci si riconduce ancora a riportare il lato di un quadrato (parallelo al primo e piu' piccolo) sulla sua diagonale:
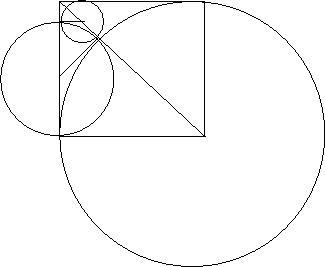 .
. - Considerando il lato del quadrato unitario, la misura numerica x della lunghezza della diagonale non potra' essere razionale. In effetti per il teorema di Pitagora dovrebbe essere x^2=2. Si e' appena visto che questa equazione non puo' avere soluzioni razionali con una costruzione geometrica che prescinde dai numeri. Si puo' facilmente trovare una prova algebrica di questo fatto:
se x fosse la frazione ``irriducibile'' m/n si avrebbe m^2= 2 n^2 , ma allora m sarebbe pari (un dispari per se stesso e' dispari! fattorizzazione unica), m=2k, e quindi 4k^2= 2n^2 cioe' 2k^2=n^2 ma allora anche n sarebbe pari come m, mentre la frazione m/n era irriducibile.
-Proprieta' teorica dei numeri razionali la densita':
tra due numeri razionali vi e' sempre un numero razionale diverso da essi
(basta prendeere la media aritmetica dei due).
-L'idea di numero come scala universale per far confronti: con i numeri si devono poter confrontare tutte le altre grandezze astratte che si usano nella pratica, anche le diagonali dei quadrati.
-Numeri reali come astrazione di successioni di misure razionali sempre piu' ``precise'' ed ``accurate''.
- Le proprieta' teoriche dei numeri reali
La completezza per successioni dei numeri reali.
dati dei numeri M1 M2, ... Mk ... al variare di k tra i naturali
1-se per ogni soglia di errore E>0 vi e e' n naturale per cui se h, k> n allora -E< Mk-Mh<E
allora vi e' un reale L per cui
2- per ogni errore E'>0 vi e' m naturale per cui se k>m allora -E'< Mk -L<E'
(qualitativamente si puo' dire che:
comunque dati infiniti numeri M1 M2, ... Mk ...
1'- che si avvicinano tra loro sempre di piu'
allora vi e' un numero L
2'- a cui si avvicinano sempre piu')
Le successioni che soddisfano la condizione 1 si dicono di Cauchy.
La condizione 2 e' la definizione della convergenza della successione a L per n che tende all'infinito, si dice anche che L e' limite della successione Mn per n che tende all'infinito.
In altre parole la proprieta' e' ogni successione di Cauchy di numeri reali converge a qualche numero reale.
La proprieta' di Archimede:
per ogni numero reale x vi e' un numero naturale n >x.
e' equivalente a: tra due numeri reali vi e' sempre un numero razionale diverso da essi
(i numeri razionali sono densi nei reali),
e' equivalente a :1/n converge a 0 per n che tende all'infinito.
5-10-09 esercitazione 2 (30 min.) Soluzione degli esercizi lasciati la precedente esercitazione.
Semifattoriali ed anagrammi. Probabilita' di avere servito un poker d'assi. Un esercizio del test di ingresso del 30/09 (altezza di una piramide a base quadrata di lato due e facce triangoli equilateri).
I numeri triangolari e la somma dei primi numeri.
6-10-09 lezione 3 ( 1 ora e 30 min.)
Riferimenti (per la lezione in oggetto): [EB] cap. 14.1 pagg. 495-498 pagg. 501-502, [MA1] cap. 3.1 pagg. 120-124 cap. 10 pagg. 525-535, [BDM] cap. 1.6 pagg. 48-56 cap 2.1-2.2 pagg. 59-71, [IRS] cap. 5
pagg.163-168 pag. 171, [VV] cap.5 pagg. 75-76.
1) Quadro dei fatti teorici enunciati:
Assiomi delle relazioni d'ordine totale.
Assiomi dei numeri naturali principio di induzione.
Numeri interi.
Teorema di fattorizzazione unica (commento sulla potenza di codifica dei numeri naturali).
Teorema di divisibilita' tra numeri interi.
Numeri razionali e densita'.
Numeri reali: completezza per successioni e proprieta' di Archimede.
Definizione di successione di numeri reali convergente ad un numero reale.
2) Interpretazione geometrica del sistema dei numeri reali:
la retta il ``continuo geometrico unidimensionale''.
Quindi le due astrazioni si fanno usualmente coincidere e si identificano i numeri reali con la retta munita di un sistema di riferimento:
- si fissa un 'origine O (lo 0)
- un verso di crescita (usualmente da sinistra a destra cosicche' un punto della retta a destra di un altro rappresenta un numero maggiore)
- un unita' di misura (il numero 1) .
Le somma tra numeri p+v si puo' identificare con un percorso lungo v a partire da p: a destra se p e' positvo a sinistra se p e' negativo.
Nota : e' importante notare che in questo caso il numero p fa le veci di un punto di partenza mentre il numero v quelle di uno spostamento o vettore.
La moltiplicazione mp nel considerare il segmento Op allungato di un fattore m, se m e' positivo, mentre se m e' negativo nel suo simmetrcio rispetto ad O.
Le proprieta' fondamentali dei numeri reali si traducono nel fatto intuitivo che la retta non ha ``buchi'' e quindi ogni numero reale e' rappresentato da qualche punto della retta, e che ogni punto della retta e' approssimabile de punti dicoordinata razionale e quindi ogni punto della retta e' associato ad un numero reale.
Appunto si dice che costituisce un continuo per cui se infiniti punti si accumulano vi deve essere un punto loro limite.
Con queste identificazioni si parlera' di retta reale.
3) Il piano e gli spazi cartesiani
Coppie, terne ordinate, ``n-ple'' ... :
(a,b)=(c,d) vuol dire a=c e b=d, analogamente per le terne ordinate etc. ...
Le coppie ordinate di numeri reali, le terne ordinate, erc. si identificano con il piano, rispettivamente con lo spazio, lo spazio n-dimensionale, muniti di un sistema di coordinate ovvero:
- fissare un punto di origine O a cui si associano le coordinate (0,0);
- fissare due rette passanti per tale punto, gli assi del sistema, e due unita' di misura su ognuna di esse;
- fissare un verso di crescita su ognuna delle due rette, semiassi positivi, e quale delle due e' la prima quale la seconda: si fissa cosi' la classe di orientamento del sistema (e.g. intuitivamente il primo semiasse positivo ruota sul secondo spazzando l'angolo convesso tra i due in senso orario piuttosto che antiorario)
quindi da un punto del piano si tracciano le parallele ai due assi e calcolando su ciascuno degli assi a che numero reale corrispondono le intersezioni si ottengono le coordinate del punto nel sistema dato;
viceversa date le coordinate si tracciano su ogni asse dalla rispettiva coordinata le parallele all'altro asse
la cui intersezione identifica un punto del piano.
Analogamente per gli spazi a piu' dimensioni
(a,b)+(c,d)= definizione (a+c, b+d)
regola del parallelogramma per la somma di vettori,
la somma con un dato vettore geometricamente rappresenta una traslazione,
Nota: quindi una coppia ordinata di numeri reali rappresenta rispetto ad un sistema di riferimento
sia un punto del piano sia una traslazione (vettore).
se r e' un numero reale r (a,b)=def. (ra , r b)
il prodotto di un vettore per un dato numero reale non negativo rappresenta una dilatazione con quel fattore,
il prodotto per -1 rappresenta la simmetria rispetto all'origine,
Usualmente un sistema di coordinate si pensa e si rappresenta pittoricamente come ``Cartesiano'':
gli angoli tra le rette siano retti,
il primo asse orizzontale ed orientato da sinistra a destra,
il secondo verticale orientato dal basso verso l'alto.
Si parlera' nel caso di spazi cartesiani.
4) Moduli, distanze e norme euclidee e distanze astratte.
- Sulla retta reale e' ragionevole definire la distanza tra due punti come la differnza tra il numero reale piu' grande con quello piu' piccolo che corrispondono ai punti
***************************************************** x- y quando x>o= y
dist(x,y)= massimo tra x e y - minimo tra x e y = ************** oppure
***************************************************** y-x quando x<o= y
si definisce quindi
|x|= dist(x,0)=massimo tra x e -x
per cui
dist(x,y)=|x-y|=|y-x|
Se pur intuitivamente ovvia e' fondamentale la seguente
|x - y| <o= |x| +|y|
(la distanza da x a y e' piu' piccola della distanza da x a 0 sommata a quella da y a 0)
equivalente a
|x+y| <o= |x| +|y| Diseguaglianza Triangolare .
- Nello spazio cartesiano ispirandosi al teorema di Pitagora si defnisce la distanza euclidea tra due punti
P di coordinate (x,y) e Q di coordinate (a,b)
dist(P,Q) = radice quadrata( (x-a)^2 + (y-b)^2)
Analogamente nello spazio cartesiano o nello spazio a piu' dimensioni
la distanza euclidea sara' la radice della somma dei quadrati delle differenze tra le coordinate omologhe.
La distanza dall'origine si dice norma euclidea e si indica come il modulo, al piu' con un indice che dichiari la dimensione:
|(x,y ... )|n = radice quadrata( x^2 + y^2 ...)
La distanza euclidea soddisfa le seguenti proprieta' generali:
dist(P,Q) > o = 0,
dist(P, Q) =dist(Q,P)
dist(P,Q) < o = dist (P,R) + dist (R , P)
dist(P,Q)=0 solo se P=Q
Distanza astratta : se in un ambiente M ad ogni coppia P e Q di elementi di M
si associa un numero dist(P,Q) in modo che queste quattro proprieta' siano soddisfatte si dice
che e' stata definita una distanza su M.
La dimostrazione della diseguaglianza triangolare per le distanze euclidee in piu' dimensioni
e' un po piu' complicata di quella per il modulo di numeri reali, pur essendo nel piano ancor piu'
trasparente il suo significato (si fa piu' strada ad andare da P a Q se si passa da un punto R, ovvero in un triangolo la somma delle lunghezze di due lati e ' maggiore della lunghezza del terzo).
Le distanze euclidee negli spazi cartesiani non sono qualsiasi distanze astratte, ma soddisfano le seguenti proprieta', rispetto alle operazioni algebriche introdotte sulle coppie, che hanno un solido corrispettivo geometrico:
dist(r P, r Q)= |r| dist (P, Q) se r e' un numero (positiva omogeneita', teorema di Talete)
dist(P+V, Q+V)= dist (P,Q) se V e' un vettore (invarianza per translazioni).
6-10-09 esercitazione 3 (30 min.)
Dimostrazione algebrica della diseguaglianza triangolare. Esercizi 1-6 test di ingresso del 8/9/09.
Esercizio lasciato: in quanti modi si scelgono k elementi tra n in modo che tra questi k ce ne siano 3 prefissati?
8-10-09 lezione 4 ( 45 min.)
Riferimenti (per la lezione in oggetto): [EB] cap. 1 e cap 2 pagg. 17-45, 55-57 , cap. 3 pagg. 59-65, 70-89, cap. 9 pagg. 234- 242, [MA1] cap. 1 pagg. 10-12, 14-20, 29-33, 42-42 1/2, 44, 47 cap. 4 pagg. 153-158 cap. 6 pagg.297-301 , [BDM] cap. 1 pagg. 11-22, 48-58, cap. 2 pag. 92, cap. 5 pagg. 179-192, cap. 8 pagg.297-301 , [IRS] cap. 2 pagg 47-52, [VV] cap. 5 pagg. 77-81, cap. 7 pagg. 48-149 .
Definizione di rapporto incrementale tra due punti (x, y) e (a, b):
il rapporto tra la differenza delle seconde coordinate b-y e la differenza delle prime coordinate a-x.
una regione del piano cartesiano in cui i rapporti incrementali tra coppie di suoi punti
sono tutti eguali e' una retta
Definizione di coefficiente angolare (o pendenza relativa) di una retta in un sistema di riferimento: e' il rapporto incrementale di una qualsiasi coppia di suoi punti.
Osservazione:
se una curva del piano cartesiano e' data implicitamente da una condizione F(x,y)=0 (per esempio x^2+y^2=9) che devono soddisfare le coordinate dei punti che stanno su di essa, per capire il suo andamento nel riferimento e' utile capire come sono messe le rette tangenti (nel caso ci siano):
retta tangente a una curva in un punto P=(a,b) come
retta la cui pendenza e' limite delle pendenze delle secanti per P=(a,b) e Q=(x,y) alla curva
quando (x,y) tende ad (a,b) rimanendo sulla curva.
Il calcolo differenziale, tra le altre cose, permette in un certo contesto di ``calcolare'' con semplici regole tali pendenze di (eventuali) tangenti.
Definizione di radice aritmetica k-esima di un numero reale x con k numero naturale non nullo:
si dice che y e' radice aritmetica k-esima di x se sono verificate le due condizioni
1)y >o= 0
2) y^k=x
Metodo di bisezione: rudimentale strumento pratico e utile ausilio teorico con il quale, grazie al postulato di Archimede e alla completezza, abbiamo accennato alla dimostrazione del seguente:
Teorema: (esistenza delle radici aritmetiche):
Se k e' un numero naturale dispari ogni numero reale x ha un'unica radice k-esima .
Se k =2m ogni numero reale non negativo ha un'unica radice radice k-esima .
Definizioni di sottinsieme limitato negli spazi euclidei e negli spazi muniti di distanza.
Definizioni di sottinsieme di R limitato inferiormente in R,
di sottinsieme di R limitato superiormente in R.
Notazione insiemistica
insieme vuoto
appartenenza e non appartenenza
due insiemi sono eguali se e solo se hanno gl istessi elementi
specificazione di un sottoinsieme { x in A : p(x) (e' vera)}
notazione per insiemi finiti {a}, {a, b}, {a_1 ... a_n}
intersezione
unione
differenza tra due insiemi
differenza simmetrica
N, Z, Q, R,
prodotto cartesiano di due o piu' insiemi
M^n (insieme delle n-ple (x_1, x_2 ... , x_n) in cui tutte le componenti sono elementi di M)
Corrispondenza tra operazioni insiemistiche e operazioni logiche : e, o , non .
Segmenti e semirette in R.
8-10-09 esercitazione 4 (45 min.) Valutare la radice quadrata di 134 con il metodo di bisezione.
Calcolare la distanza tra (1,2,3) e (7, 9 ,10).
Provare che 2^n > n.
La successione 1/2^n tende a 0 per n --> + oo.
Provare che per n abbastanza grande 2^n > 1000 n +10^9.
Provare che al variare di n e m tra i numeri naturali non nulli l'insieme dei valori
mn/(m^2+n^2) e' limitato.
Esercizi lasciati: al variare di x e y tra i numeri reali positivi trovare il miglior limite superiore
e il miglior limite inferiore all'iniseme dei valori xy/(x^2+y^2).
12-10-09 lezione 5 ( ore 1 e 15 min. )Riferimenti: [EB] cap. 1 pagg. 17-45 , cap. 6 pagg. 143-147, 152-162, [MA1] cap. 4 curiosita' 4.1 pag. 160, cap. 1 pag. 9-11, cap.5 pagg. 232, 240- 242, 244-245,
[BDM] cap. 1 pagg. 37-38, 40, cap. 6 pagg. 215-235, [VV] cap. 4 pagg. -70 , cap. 6 pagg. 102-119.
Notazione per la relazione di inclusione (contenuto o eguale) tra insiemi.
Estremo superiore, estremo inferiore versus massimo e minimo
La completezza sequenziale ``piu' '' il postulato di Archimede
sono equivalenti al seguente enunciato
ogni sottoinsieme di R
non vuoto e limitato
ammette in R
estremo superiore ed estremo inferiore
Potenze frazionarie
Definizione, esistenza, proprieta' algebriche e di ordinamento di
esponenziale e logaritmo
12-10-09 esercitazione 5 (45 min.) Svolgimento dell'esercizio lasciato, disequazioni con trinomi di secondo grado, esempio di sistema di diseguaglianze.
13-10-09 lezione 6 ( ore 1)
Riferimenti: [EB] cap. 3 pagg. 70-89, cap.5 pagg. 111-113, 116, [MA1] cap. 6 pagg. 298-300, cap.5 pagg. 257-258, [BDM] cap. 2 pag. 67, 75-78, 92-95, cap. 4 pagg. 152-155 cap.5 pagg. 179-192, [VV] cap. 4 pagg. 77-80.
- Misure matematiche
Pseudoanello di insiemi: un insieme M di sottoinsiemi di un insieme M per cui
A) vuoto sta in M
B) se A e B stanno in M anche le loro: unione, intersezione e differenza stanno in M .
Proprieta' di una misura m (finitamente) additiva su uno pseudoanello di insiemi
1) m(A) e' un numero reale non negativo
2) m(vuoto)=0
3) m(AUB) =m(A) +m(B)- m(A intersezione B)
di conseguenza
4) se A e' contenuto in B si ha m(A) =o< m(B)
Intervalli = segmenti, semirette, rette
Lunghezza di segmenti: la differenza tra estremo superiore ed estremo inferiore del segmento.
n-rettangoli cartesiani: in R^n un n rettangolo cartesiano e' il prodotto di insiemi di n segmenti
quindi e' il sottoinsieme di R^n i cui elementi hanno i-esima coordinata nell'i-esimo segmento
Misura elementare di n-rettangoli cartesiani: il prodotto delle lunghezze dei ``lati''
Per un sottoinsieme A, di uno spazio cartesiano, limitato e non vuoto si definiscono
``misura superiore'' di Peano Jordan
m^* (A) = inf{ somme delle misure degli n-rettangoli R_1 ... R_k
al variare di k in N e di R_1 ... R _k in modo che la loro unione contenga A}
``misura inferiore'' di Peano Jordan
m_*(A)= sup{ somme delle misure degli n-rettangoli Q_1 ... Q_h
al variare di h in N e di Q_1 ... Q _h in modo che la loro unione sia contenuta A
e le loro intersezioni a due a due siano di dimensione minore}
I misurabili di Peano Jordan sono i sottoinsiemi A per cui m^*(A) = m_* (A).
Formano uno pseudoanello di sottoinsiemi degli spazi cartesiani
Nel caso il valore comune si dice misura di Peano Jordan n-dimensionale di A: m_n(A).
Imponendo che la misura di Peano-Jordan del vuoto sia nulla si ha che
la misura di Peano-Jordan e' una misura, inoltre non solo verifica 1),2), 3), 4) ma anche
ulteriori proprieta' (geometriche) della misura di Peano-Jordan n-dimensionale
5) m({ tv: v in A}) = |t|^n m(A) (positiva omogeneita' della misura)
6) se R(A) e' il ruotato di A allora m(R(A))=m(A) (invarianza per rotazioni)
7) m({ v+w: v in A}) =m(A) (invarianza per traslazioni)
Misura di insiemi non limitati:
si devono poter misurare le intersezioni dell'insieme non limitato con palle di raggio R
quindi si fa il limite di tali misure per R-->+oo.
Definizione:
Pigreco (pig) e' la misura bidimensionale di Peano-Jordan di un cerchio di raggio 1.
La lunghezza di un arco di circonferenza di raggio R e' eguale
a 2R per l'area del settore delimitato.
- Retta passante per un punto e coefficiente angolare dato (insieme dei punti le cui coordinate
hanno rapporto incrementale con il punto dato eguale al coefficiente angolare dato)
Forma generale di una retta.
Grandezze trigonometriche:
- dal punto divista geometrico sintetico :
descrizione di sottoinsiemi mediante condizioni che devono essere soddisfatte dalle coordinate
complementarieta' della dimensione di un sottoinsieme dello spazio cartesiano
e del numero di condizioni ``indipendenti'' necessarie a descriverlo.
primo cenno alla descrizione di una regione (unidimensionale) come cammino
e.g.
semicirconferenza x tra 0 e 1 ---> (x, radiceq{ 1-x^2})
semipiani ed angoli nel piano definiti tramite diseguaglianze.
-seno e coseno di un numero reale:
se x e' tra 0 e pigreco:
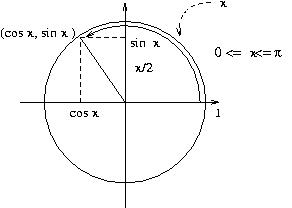
(cos x, sin x) sono le coordinate del secondo estremo Q dell'arco,
a partire da P(1,0) sulla circonferenza unitaria di centro l'origine
percorso in senso antiorario, che sottende un settore di area x/2 (di lunghezza x)
se x e' tra -pigreco e 0: cos x=cos (-x), sin x=-sin(-x)
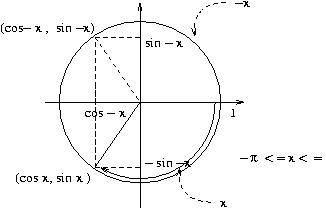
per gli altri x in R :
sia k in Z per cui -pigreco <=o x - 2kpigreco <o= pigreco
cos x =cos (x- 2kpigreco), sin x =sin (x- 2kpigreco)
NOTA aggiunta: andrebbe provato che per ogni numero reale x tra 0 e pig vi e' l'arco,
a partire da P(1,0) sulla circonferenza unitaria di centro l'origine
percorso in senso antiorario, che sottende un settore di area x/2 (di lunghezza x).
13-10-09 esercitazione 6 (ore 1) strisce nel piano, rettangoli cartesiani, diseguaglianze per definire un semipiano, diseguaglianze per definire un angolo, la misura bidimensionale di un segmento e' nulla, la lunghezza di una arco di circonferenza unitaria e' il doppio del settore circolare da esso delimitato.
Esercizio lasciato trovare le coordinate del punto di intersezione delle rette definite dalle equazioni y=-x-4
e y=3x+5
15-10-09 lezione 7 ( ore 2) Riferimenti: [EB] cap.5 pagg. 113,-130, 139-141, cap 14 pagg. 498-511, [MA1] cap.5 pagg. 262-266 cap. 10 pagg. 535-541, [BDM] cap. 2 pagg. 75-79, 81-87, 95-99 cap.5 pag. 198 cap. 6 pagg. 235-244, 246-251, [IRS] cap.5 pagg. 169-174, 177, [VV] cap. 4 pagg. 77-80 cap. 6 pagg. 119-128.
NOTA : questa lezione contiene un argomento presumibilmente nuovo per gli studenti del corso, e che e' di fondamentale importanza:
nozione significato geometrico e proprieta' algebriche del prodotto scalare
Proprieta' delle grandezze trigonometriche:
Definizione di tangente: tan x = sin x / cos x
per x diverso da pigreco/2 + k pigreco per tutti i k in Z .
La tangente di x e' quindi la pendenza della semiretta dall'origine (0,0) al punto di coordinate
(cos x , sin x), pertanto e' anche la seconda coordinata del punto di intersezione di questa con la retta
verticale per (1,0) (tangente alla circonferenza).
Radianti e gradi (cenno)
Formule trigonometriche PDF :
In margine a quanto allegato nel link vale la pena sottolineare quanto osservato a lezione:
- si ha sempre -1 < o = cos x <o= 1 e -1 < o = sin x <o= 1
come conseguenza della prima formula cos^2 x+sin^2 x=1
che esprime il fatto che (cos x,sin x) sono le coordinate di un
punto sulla circonferenza unitaria di centro (0,0)
- si ha sempre cos (x +2k pig) =cos x , sin (x+2k pig ) =sin x
come conseguenza diretta della definizione
- e dalla caratterizzazione geometrica tan x = tan ( x + k pigreco) per tutti i k in Z .
- Oltre quanto detto a lezione e' importante notare
se a^2 +b^2= 1 allora vi e' x per cui a =cos x , b = sin x
se a^2 +b^2= 1 allora vi e' un unico x nell'intervallo [q ; q+2 pig[ per cui a =cos x , b = sin x
-Si riporta, per completezza, la dimostrazione delle formule di addizione, non svolta a lezione, nel caso particolare illustrato dalla figura (x+y < pig /2 ) e del seno:
cos (x+y)=cos x cos y - sin x sin y, sin (x+y)= sinx cos y+cos x sin y

osservando che il triangolo di altezza H=sin (x+y) sul lato z e'
il triangolo di altezza h sul lato b
imponendo che le aree siano eguali si ha Hz= hb cioe' H =hb/z
osservando inoltre che h =cos y= z cos x e b= sin y + z sin x
si ottiene quanto desiderato:
sin (x+y)=(sin y + z sin x) cos x = sin y cos + z cos x sin x = sin y cos x + cos y sin x.
Definizione: una grandezza F che dipende da una grandezza descritta la variare di x in R
si dice periodica di periodo T se F(x+T)=F(x)
Problema: esprimere mediante le coordinate di due vettori v=(x_1, ... , x_n), w=(y_1, ... , y_n),
le grandezze trigonometriche relative all'angolo che essi formano con l'origine O= (0, ..., 0)
Prodotto scalare
Espressione del coseno dell'angolo vOw in termini delle coordinate
Preliminari
rette in forma parametrica [lineare] (come percorso di un cammino rettilineo [a velocita' costante])
- per una retta nel piano cartesiano passante per l'origine r={(x,y): a x + by=0}:
si considera un vettore w le cui coordinate sono di un punto sulla retta
(per esempio w=(-b, a))
tutti i punti t(-b,a) al variare di t in R stanno sulla retta;
viceversa ogni punto per cui ax+by=0 e' del tipo t(-b,a) (x= -bt, y= ta) per qualche t in R.
quindi r={ tw : t in R}
cioe' una retta per l'origine e' data dai multipli reali delle coordinate di un qualsiasi vettore w
le cui coordinate soddisfano la condizione ax +by=0:
il vettore puo' essere interpretato come velocita' costante (in verso e intensita') con cui si percorre la retta data a partire da O (vettore dall'origine)
-per una retta non passante per l'origine r={(x,y): a x + by +c=0} c non 0:
si considera r' parallela ad r passante per O per esempio l'insieme dei punti t (-b,a), al variare di t in R
si considera un punto P che sta sulla retta (per esempio P=(0, -c/b))
quindi r= r'+P = { tw +P: t in R}= { t(-b,a) +(0, -c/b): t in R}= { (-tb , ta -c/b): t in R }
cioe' una retta non per l'origine e' data dai multipli reali delle coordinate di un qualsiasi vettore ad essa parallelo sommate alle coordinate di un qualsiasi punto appartenente alla retta
il vettore puo' essere interpretato come velocita' costante (in verso e intensita') con cui si percorre la retta data a partire da P (vettore ``applicato a P'').
- Quindi dato un vettore w=(y_1, ... , y_n) e un punto P =(q_1, ... , q_n)in R^n l'insieme
r={ tw +P: al variare di t in R}={ (ty_1+q_1, ... , ty_n + q_n) : al variare di t in R}
rappresenta una retta parallela a w e passante per P
w puo' essere interpretato come velocita' costante (in verso e intensita') con cui si percorre la retta data a partire da P.
il valore minimo di un trinomio di secondo grado:
(dimostrazione leggermente diversa, per semplicita' di edizione dattilografata, rispetto a quanto svolto a lezione)
Dati A>0, B e C in R
si consideri l'insieme dei numeri {z: z= At^2 +B t +C per qualche t in R}
in forma abbreviata si considera l'insieme dei valori At^2 +B t +C: t in R
ci si chiede se vi e' un t per cui la grandezza assuma un valore minimo e nel caso
quali siano i t per cui cio' avviene e quale sia il valore minimo
si procede come segue si cerca di scrivere la grandezza come (at+b)^2 +c
nel caso c'e' il valore minimo =c e vi e' un unico t per cui si assume questo valore t = -b/a
per determinare a, b, c
si impone (at+b)^2 +c = At^2+Bt +C per ogni t in R
per t =0 si ottiene la relazione b^2 +c =C cioe' c= C-b^2
svolgendo il quadrato e utilizzando questa relazione la condizione da verificare diventa
a^2 t^2 +2abt = At^2 +Bt p.o. t
considerando t non nullo e dividento si ha a^2 t +2ab =At+B p.o. t non 0
cioe' (a^2- A)t =B-2ab p.o. t non 0
ma uno dei due termini dell'identita' non dipende da t mentre l'altro e' un multiplo di t
quindi perche' l'identita' si valida per ogni t non 0 devono essere entrambi nulli
a^2= A
B=2ab
da cui si ricava a= radiceq( A ) , b= B/2radq(A) e dalla prima c= C- B^2/4A
e quindi vi e' valore minimo di At^2+Bt +C eguale a C-B^2/4A assunto per t =-B/2A
Espressione del coseno dell'angolo vOw con le coordinate di v=(x_1, ... , x_n) e w=(y_1, ... , y_n)
(si propone una dimostrazione leggermente diversa e piu' completa di quanto svolto a lezione)
per comodita' se u ha coordinate (z_1, ... , z_n) indichiamo con
|u| = distanza dall'origine = radice della somma dei quadrati delle coordinate
= radiceq(z_1^2 + ... z_n^2)
- ci si mette nel piano individuato da O, v=(x_1, ... , x_n) e w=(y_1, ... , y_n)
- sia D la minima distanza di v dalla retta tw, t in R,
sia P il punto di minima distanza di v dalla retta tw, t in R
in particolare P ha coordinate del tipo L w
dato che su una circonferenza di raggio R la proiezione perpendicolare di un estremo di una corda sul raggio (orientato positivamente) dal centro all'altro estremo e' R cos (angolo al centro)
considerando R=|v|
|v| cos vOw = L|w|, cioe' cos vOw = L|w|/ |v|
- d'altra parte D=distanza(v, P) =distanza (v , Lw) = Minimo {distanza w, tw); al variare di t in R}
per esprimere esprimere cos vOw con le coordinate dei due punti basta
esprimere L in termini di essi
ma D^2 e' il minimo di una grandezza del tipo At^2+Bt +C vediamo:
D^2= (Minimo {distanza(v, tw): al variare di t in R})^2= [il quadrato del minimo e' il minimo dei quadrati]
= Minimo { (distanza (v,tw))^2 : t in R} =
= Minimo { |v-tw|^2 : t in R}=
= Minimo { (x_1 -ty_1)^2 ... ,+ (x_n -t y_n)^2 : t}=
= Minimo { x_1^2 + t^2y_1^2 - 2 tx_1 y_1 + ... + x_n^2 + t^2y_n^2 - 2 tx_n y_n : t}=
= Minimo { t^2 somme y_i^2 - 2 t somme x_i y_i + somme x_i^2 : t}=
= Minimo {t^2 |w|^2 - 2 t somme x_i y_i + |v|^2 : t } = [A=|w|^2, B=-2 somme x_i y_i , C=|v|^2]
= C-B^2/4A = |v|^2 - 4 (somme x_i y_i )^2 /4|w|^2
valore assunto come ben sappiamo per t=T = -B/2A =somme x_i y_i / |w|^2
quindi Lw= P= Tw e L = somme x_i y_i / |w|^2
da cui si deduce la relazione cercata: cos vow= L|w|/|v|= somme x_i y_i / |w||v|
x_1 y_1 + ... + x_n y_n
cos vow = ---------------------------------------------------------------------------------- radq( x_1^2 +...+ x_n^2) radq( y_1^2 +...+ y_n^2)
NOTA: come si vedra' il coefficiente di correlazione in statistica descrittiva e' proprio il coseno di un angolo espresso con questa relazione.
Definizione:
Prodotto scalare, o prodotto (vettoriale) interno, cartesiano o euclideo
tra v=(x_1, ... , x_n) e w=(y_1, ... , y_n):
e' il numero reale dato dalla somma dei prodotti delle coordinate di stesso posto
x_1y_1 + ... + x_ny_n
esso si indica con v.w = x_1y_1 + ... + x_ny_n o con (v|w ) o con <v,w>
Riassumendo quanto descritto si ha quindi
(v|w )
cos vow = ---------------- |v| |w|
il coseno dell'angolo tra due vettori non nulli di R^n e' il rapporto tra loro prodotto scalare e prodotto delle loro norme.
Due vettori saranno ortogonali se il loro prodotto scalare si annulla.
Quindi due vettori sono tra essi perpendicolari se e solo se il prodotto scalare tra di essi si annulla
Piani nello spazio e rette nel piano
L'equazione di una retta ax+by+c=0 oltre ad esser interpretata come fatto la lezione scorsa
come condizione che garantsce che i rapporti incrementali di coppie di punti su di essa siano costanti
ora ha un trasparente significato come condizione di ortogonalita'
(x,y) per cui ax+by=(a,b).(x,y)=0 sono i punti il cui vettore e' ortogonale ad (a,b)
quindi la retta {(x,y): ax+by =0 } e' la retta dei ``multipli reali'' di (-b,a) (vettore ortogonale a (a,b))
quindi
se ap +bq +c =0 cioe' c=-ap-bq cioe' se (p,q) sta sulla retta
i punti (x,y) della retta per cui ax+by+c =0 sono quelli per cui (x-p, y-q) e' ortogonale ad (a,b)
quindi la retta {(x,y): ax+by+c=0} e' la retta parallela a t(-b,a), t in R passante per (p,q)
Cio' considerato l'insieme N={(x,y,z): ax +by +cz +d =0} se (p,q,r) e' un suo elemento
N={(x,y,z) : (abc). (x-p, y-q, z-r)=0}
non e' altro che l'insieme dei punti (x,y,z) per cui (x-p, y-q, z-r) e' ortogonale a (a,b,c)
e quindi e' il piano ortogonale ad (a,b, c) passante per (p,q,r).
In generale in R^n l'insieme N={(x_1, ... , x_n) : a_1 x_1+ ... + a_n x_n +k=0}
se P=(y_1, ... , y_n) e' un suo punto
N={(x_1, ... , x_n) : (a_1, ... ,a_n) . (x_1-y_1, ... , x_n - y_n) =0}
puo' essere interpretato come piano (n-1)-dimensionale ortogonale
a (a_1, ... , a_n) e passante per P (y_1, ... ,y_n): iperpiano= piano con una diemnsione in meno rispetto allo spazio ambiente.
Proprieta' algebriche del prodotto scalare
Una grandezza che a due vettori cartesiani v e w fa corrispondere un numero reale B(v,w)
si dice bilineare se
B(v+u , w) = B(v, w) + B(u, w)
B(v , u+w) = B(v, u) + B(v, w)
B(tv , w) = B(v,t w) = t B(u, w) se t e' un numero reale
si dice simmetrica se
B(v , w) = B(w,v)
si dice semidefinita positiva se
B(v , v) > o= 0
si dice definita positiva se
e' semidefinita positiva e B(v , v)= 0 se e solo se v=O
Direttamente dalla definizione e dalle proprieta' di somma e prodotto di numeri reali
il prodotto scalare B(v,w)= v.w e' una grandezza
bilineare
simmetrica
definita positiva
si noti ancora che v.v = |v|^2
Con queste prooprieta' e' agevole il calcolo simbolico che coinvolge norme al quadrato prodotti scalari
senza coinvolgere le coordinate
(l'unica accortezza e' tener presente che il prodotto scalare di due vettori e' un numero reale)
per esempio: utilizzando la bilinearita' e la simmetria si ottiene subito la formula per la norma al quadrato
della somma di due vettori
|v+w|^2 = (v+w).(v+w) = v.v + 2 v.w + w.w = |v|^2 + 2 v.w + |w|^2
del tutto analoga alla formula valida per due numeri
Definizione:
una grandezza vettoriale L(v) che dipende da v vettore si dice
lineare se
L(v+t w) = L(v) + t L(w) per ogni numero reale t.
Esercizio lasciato:
Esprimere seno, coseno, tangente di x in termini del seno di x/2
19-10-09 lezione 8 ( ore 1)
Riferimenti: [EB] cap.5 pag. 137, 138, cap. 14 pag. 480, (pagg. 498-551 gia' segnalato) pagg.522-524,
problemi 14.2.1-2, 14.2.5-10, 14.2.29-30, 14.4.1-5.4, 14.8.1-6, [MA1] cap.5 267-268, cap.10 (pagg. 525-541 gia' segnalate) pagg. 542-545, 550-552 ed esercizi relativi, [BDM] cap.2 (pagg. 92-97 gia' segnalate) esercizi 2.1--18, cap. 6 pagg. 247-251 esercizi 6.1-6, 6.10-15, 6.18, [IRS] cap.5 (pagg. 165-174 gia' segnalate) pagg. 177-178, pagg.188-190, [VV] cap. 4 (pagg. 62-70 gia' segnalato) cap. 5 pag. 77, cap. 6 pag. 124.
Diseguaglianza di Cauchy-Schwarz: nel caso del prodotto scalare cartesiano direttamente dalla sua interpretazione geometrica:
|(v|w )|_1 < o = |v|_n |w|_n
( | x_1 y_1 + ... + x_n y_n| < o = rad( x_1 ^2 + ... + x_n ^2) rad( y_1 ^2 + ... + y_n^2) )
Dimostrazione della diseguaglianza triangolare per le distanze euclidee.
Iper-piani espressi con condizioni di ortogonalita'.
Come cambiano le coordinate cambiando l'origine:
formula per calcolare la distanza di un iperpiano, espresso con una condizione di ortogonalita' x.A=c
, da un punto Q (in grassetto i vettori):
|Q.A - c|_1
--------------------------
| A |_n
Giacitura di un (iper-)piano nello spazio (n dimensionale).
Scrittura parametrica, non unica, di un (iper-)piano nello spazio (n-dimensionale):
t_1 u_1 + t_2 u_2 + ... + P, al variare di t_1, t_2 ... in R,
(in grassetto i vettori)
se la condizione di definizione del piano e' x.A=c
fissate le coordinate di un punto P del piano
P.A=c
fissate le direzioni non allineate (``indipendenti'') ortogonali all'ortogonale del piano, ovvero a lui parallele,
u_1 .A=0 , u_2.A=0 ,...
si ha sul piano in questione un sistema di riferimento i parametri (t_1, t_2 ... ) che descrivono gli altri punti del piano sono le coordinate, rispetto a tale sistema,
cioe'
le ``lunghezze con segno'' (avendo come unita' di misura |u_1|, |u_2| ...) dei lati (paralleli a u_1, u_2 ... ) delle spezzate per raggiungere il punto del piano a partire da P.
Interpretazioni geometriche dei ``sistemi di primo grado con k e quazioni e n incognite''
1-interpretazione: intersezione in R^n di (al piu') k iperpiani
se k < o= n, e le k condizioni sono ``indipendenti'' si otterra' un oggetto n-k dimensionale
2-interpretazione: il vettore in R^k dei termini noti in che modi puo' essere espresso come somma di multipli degli n vettori di R^k dati dalle ``k-puple'' dei coeffcienti di ognuna delle n variabili
ovvero
come raggiungere (ordine dei lati a parte) il vettore dei termini noti muovendosi su una spezzata con lati paralleli ai vettori dati dai coefficienti di ciascuna variabile
N.B. vi saranno altre interpretazioni geometriche dei sistemi del primo ordine.
La nozione di ``indipendenti''
che nel caso di due vettori si riduce a quella di essere non paralleli, cioe' non essere uno multiplo
dell'altro,
sara' specificata nelle lezioni seguenti e sara' una nozione fondamentale.
19-10-09 esercitazione 7 (ore 1)
Scritture in forma parametrica della retta specificata da 3x+2y=151.
Distanza dell'origine dalla retta specificata dalla condizione 3x+2y=151 usando la perpendicolarita'.
Distanza del punto (1,2) dalla stessa idem.
Considerazioni teoriche per arrivare alla formula generale.
Scritture in forma parametrica del piano specificato da 3x+2y+5z=151.
Filosofia: dal procedimento in cui si ha una intuizione condivisible e diretta (geometrica in dimensione bassa) si passa ad una formula che ha validita' in ambito piu' astratto e generale ove potrebbe
esser difficoltoso avere un'intuizione condivisibile (spazi a piu' dimensioni anche infinite).
Cenno: certi spazi a dimensione infinita si possono trattare con questi metodi cartesiani
a patto che le coordinate abbiano serie dei quadrati dei coefficienti finite.
20-10-09 lezione 9 ( 45 min.)
Riferimenti: per questa lezione, che espone le nozioni astratte che danno ``il consuntivo'' di quanto esposto in precedenza, conviene basarsi su quanto di seguito esposto. Qulche nozione si trova [MA1] cap. 10 pag. 528 curiosita' 10.1, pag. 538 cur. 10.2, pag. 553 cur. 10.4, pag. 571.
Spazio vettoriale su R astratto:
in un insieme V si ha una struttura di spazio vettoriale su R se si definiscono due operazioni
1- la prima che trasforma una coppia di elementi di V in un elemento di V
usualmente indicato e chiamato somma dei due: (u,v) in VxV -----> u+v in V
2- la seconda che trasforma una coppia (numero reale, elemento di V) in un elemento di V
usualmente indicato e chiamato prodotto dei due: (r, v) in RxV -----> r.v in V
per cui:
la somma e'
commutativa: u+v=v+u
associativa: u+(v+w)=(u+v)+w
ha elemento neutro in V, che si indica con 0_V : u+ 0_V = u
ogni elemento u ha un opposto v, indicato con -u, per tale somma : u+(-u) = 0_V ;
il prodotto e'
associativo rispetto al prodotto di numeri reali: (rs). v=r.(s.v)
distributivo rispetto alle somme: r.(u+v)= r.u +r.v, (r+s).v= r.v + s.v
ha come elemento neutro 1: 1.v=v
Si deducono direttamente ``usuali'' regole di calcolo: (-1)u= -u, 0.u =0_V ...
L'idea e' quella di R^2:
lo stesso oggetto, coppia di numeri reali u=(a,b), indica sia una posizione nel piano, rispetto ad un sistema di coordinate, sia una traslazione di punti del piano (x,y)----->(x+a,y+b).
La nozione astratta di spazio vettoriale con questo principio individua una classe particolare di strutture ove la situazione piu' generale
uno spazio di posizioni P ,
un ``gruppo '' T di traslazioni di elementi di P,
un ``campo'' D di dilatazioni (di dato centro) di elementi di P,
si semplifica identificando l'azione degli elementi di T su P mediante la ``somma'' tra elementi di P, e D con i numeri reali.
Esempio: oltre agli spazi cartesiani R, R^2, ... , R^n, i polinomi di una variabile a coefficineti in R con le usuali regole di calcolo su di essi, sono una struttura di spazio vettoriale reale che si indica con R[x].
Osserviamo, per ora intuitivamente, che tale spazio dei polinomi ha dimensione infinita, contrariamente agli spazi cartesiani.
Identificando un polinomio con la ``ennnupla'' dei suoi coefficienti, ordinati per esempio secondo il grado
della variabile che moltiplicano, R[x] e' (a meno di identificazioni) l'unione di tutti gli R^n.
Prodotti scalari astratti.
In uno spazio vettoriale, come vedremo sara' agevole parlare di rette parallele, piani, ``piani '' di dimensione k etc. .
Ma, come si vede gia' dall'arbitrarieta' di identificare, come uso, R^2 con il piano cartesiano ad assi perpendicolari e eguali unita' di misura su di essi, ``l'alfabeto'' degli spazi vettoriali non permettere di
esprimere nozioni di distanza che siano indipendenti dalla direzione, ne, tanto meno una nozione di misura dell'angolo tra vettori.
Per ottenere cio' va aggiunta alla struttura di spazio vettoriale la nozione di prodotto scalare astratto che si ricava dalle proprieta' di calcolo del prodotto scalare cartesiano tra elementi di R^n.
Definizione :
su uno spazio vettoriale V si ha un prodotto scalare se
a ogni coppia v e w di elementi di V si fa corrispondere un numero reale B(v,w) = v._B w in modo che
tale associazione sia:
bilineare B(v+u , w) = B(v, w) + B(u, w) (distribuitvo rispetto alla somma)
B(v , u+w) = B(v, u) + B(v, w)
B(tv , w) = B(v,t w) = t B(u, w), t in R (omogeneo, associativo con il prodotto per numero)
simmetrica B(v , w) = B(w,v)
semidefinita positiva B(v , v) > o= 0
definita positiva B(v , v)= 0 se e solo se v=O_V
Un prodotto scalare astratto ha quindi tutte le regole di calcolo usuali del prodotto tra numeri utili come visto nel caso del prodoto scalare cartesiano.
L'accortezza e' che i fattori sono vettori mentre il risultato e' un numero.
Diseguaglianza di Cauchy-Schwarz in astratto: se v._B w e' un prodotto scalare su V si ha
| v._B w |^2 < o = ( v._B v) (w._B w )
inoltre l'eguaglianza si ha solo nel caso in cui v e' multiplo di w .
La dimostrazione non puo' essere quella mostrata per il prodoto scalare cartesiano che usava l'eguaglianza del rapporto dei termini della diseguaglianza con il coseno al quadrato. Si usano direttamente le prorpieta' di un prodotto scalare:
se v e' multiplo di w si ha l'eguaglianza
altrimenti per ogni numero reale t si ha
0 < (definito positivo) (v+tw)._B (v+tw) = (distibutivita') v._B (v+tw) + (tw)._B (v+tw)
= (distribuitvita') v._B v + v._B (tw) + (tw)._B v + (tw)._B (tw) =
= (omogeneita') v._B v + t (v._B w) + t( w._B v )+ t^2(w._B w) =
= (simmetria) (w._B w)t^2 + 2 (v._B w) t + v._B v
ma un trinomio di secondo grado e' sempre (per ogni t) positivo solo se il suo discriminante e' negativo
4 (v._B w)^2 < 4 (w._B w) ( v._B v )
Se, infine, si ha l'eguaglianza, cioe' il discriminante e' nullo, (v+tw)._B (v+tw) si annulla per t eguale
a -2 (v._B w)/(w._B w).
Distanza derivata da un prodotto scalare :
Se v._B w e' un prodotto scalare su V allora: dist_B (v,w)=rad((v - w)._B ( v-w))
e' una distanza su V:
dist(u,v) > o = 0,
dist(u, v) =dist(v,u)
dist(u,v) < o = dist (u,w) + dist (w , v)
dist(u,v)=0 solo se v=u
invariante per traslazioni: dist(u,v) = dist(u+w, v+w) = dist (u-v, O_V )
e positivamente omogenea: dist(tu, tv) = |t| dist(u,v)
Con |v|_B si indica dist_B( v, O_V) = rad(v ._B v) chiamata norma relativa al prodotto scalare.
Il calcolo piu' impegnativo e' quello relativo alla verifica della diseguaglianza triangolare, essendo
gli altri conseguenze dirette delle proprieta' del prodotto scalare. Per avere la diseguaglianza triangolare
vista l'invarianza per traslazioni, e ' sufficiente mostrarla per la distanza dall'origine quindi basta provare
|v +w|_B < o = |v|_B + |w|_B
essendo i termini della diseguaglianza non negativi e' equivalente provare la diseguaglianza per i loro quadrati, utilizzando le proprieta' del prodotto scalare che permettono di usare l'usuale formula del quadrato di una somma, il quadrato del primo termine e'
v._B v + w._B w + 2 v._B w
mentre il quadrato del secondo termine e': |v|_B ^2 + |w|_B ^2 + 2|v|_B |w|_B,
quindi semplificando i quadrati grazie alla diseguaglianza di Cauchy-Schwarz si ottiene quanto desiderato.
Definizione: in un spazio vettoriale V munito di prodotto scalare v._B w si definisce
il coseno (relativo al prodotto scalare dato) tra u e w con il rapporto tra
v._B w e |v|_B |w|_B.
Identita' del parallelogramma: in un spazio vettoriale V munito di prodotto scalare v._B w
si ha
|v + w|_B ^2 + |v-w|_B ^2 = 2 ( |v|_B ^2 + |w|_B^2 )
si ripropone in astratto il teorema di geometria euclidea che stabilisce
che la semisomma dei quadrati delle diagonali di un parallelogramma e' eguale alla somma dei quadrati dei lati.
Questa e' una condizione necessaria affinche' una distanza invariante per traslazioni ed omogena derivi da un prodotto scalare.
In effetti vale il viceversa
Teorema: una distanza invariante per traslazioni ed omogenea deriva da un prodotto scalare se vale l'eguaglianza del parallelogramma.
Nel caso il prodotto scalare non puo' che essere: 1/4 ( |v + w|_B ^2 - |v-w|_B ^2 ).
Definizione: una trasformazione T tra due spazi vettoriale V e W si dice lineare se
T(u +_V v) =T(u) +_W T(v) (additiva, si distribuisce sulla somma,)
T(r._V u ) = r._W T(u) (omogenea, commuta con il prodotto per un numero)
In particolare si ha T(O_V)= O_W , cioe' l'origine di V viene trasformata nell'origine di W.
Teorema fondamentale dell'algebra lineare: in uno spazio vettoriale V che abbia due vettori non paralelli,le trasformazioni lineari per cui ogni punto e' il trasformato di un solo altro punto
sono tutte e sole
le trasformazioni per cui: ogni punto e' il trasformato di un solo altro punto, l'origine rimane fissa, ogni retta viene trasformata in una retta.
.
20-10-09 esercitazione 8 (ore 1 e 15 min.)
- date le coordinate di tre punti in R^4 calcolare l'area del triangolo che li ha come vertici
area triangolo di vertici u, v, w = 1/2 rad{ |v-u|^2 |w -u|^2 - ((v-u).(w-u))^2 }
-quanti sono i piani (bidimensionali) coordinati in R^4
quanti sono gli spazi k-dimensionali coordinati in R^n
-calcolare l'area e perimetro del triangolo isoscele di lato 2 e angolo al vertice pig/4
calcolare l'area del triangolo inscritto nel settore circolare di ampiezza pig/6 e raggio 3
calcolare l'area di tale settore circolare e la lunghezza dell'arco di circonferenza da esso determinato
-risolvere sin (3x) > 1/2
-si consideri nel piano cartesiano il nuovo sistema di riferimento con egual origine, avente primo asse e relativa unita' di misura determinati dal vettore (2,2), e secondo asse e relativa unita' di misura determinati dal vettore (3,1). Calcolare le coordinate di un punto (a,b) nel nuovo sitema di riferimento.
Si esprima il nuovo prodotto scalare cartesiano dato dalle nuove coordinate mediante le vecchie.
-Si provi che dist((a,b), (x,y))= |a-x|+|b-y| e' una distanza su R^2 invariante per traslazioni e positivamente omogenea.
-Si mostri che tale distanza non deriva da nessun possibile prodotto scalare.
21-10-09 esercitazione 9 (ore 2)
-esercizi n. 7-10, 12-17 test di ingresso ``linguaggio matematico di base, modllizzazione, ragionamento''
-risoluzione grafica di diseguaglianze
26-10-09 lezione 10 ( 45 min.) In questa lezione si sono introdotti degli elementi teorici utili per gli esercizi svolti nella esercitazione odierna.
Riferimenti per logica: [EB] cap. 2 pagg.45-58; [MA1] cap.1 pagg. 33-37, 47-48;
Riferimenti per i primi elementi di calcolo delle probabilita':
[EB] cap.13 pagg.401-412, pagg. 419-423
le pagine 413-419 convien leggerle ora anche se alcuni concetti verranno spiegati in successive lezioni,
pagg. 431-439;
[MA1] cap.2 pagg.49-69, 91-101, 106;
[BDM] cap.10 pagg.391-396, 399-407, 422-426
ancora legger ora pagg.413-422 che in parte sono state spiegate e lo saranno completamente in seguito,
cap.11 pagg.427-434;
[IRS] cap 1.5 pagg. 13-24,
legger ora 1.5.2 pag. 19 di cui si si parlera' ancora in seguito
cap. 1.6.5 pagg. 37-39;
[VV] cap. 11 pagg. 239-249
legger ora cap. 11.2 pagg. 249-259 la cui spiegazione in classe sara' ripresa in seguito.
-Calcolo proposizionale: in quest'ambito non ci interessa cosa sia una proposizione ma come si trasformano i valori di verita' con i connettivi logici ``e, o, non , =>''
Calcolo proposizionale e tavole di verita'
proposizione | P | non P|
----------------------
valore di verita' | Vero | Falso |
| F | V |
| P | Q | P e Q |
|V | V | V |
|V | F | F |
|F | V | F |
| F | F | F |
| P | Q | P o Q |
|V | V | V |
|V | F | F |
|F | V | F |
| F | F | F |
ex falso sequitur quodilibet: se P allora Q
| P | Q | P => Q |
|V | V | V |
|V | F | F |
| F | V | V |
| F | F | V |
``P=> Q'' e' equivalente a
``(non P) o anche Q'' equivalente a
``(non P) o(non (non Q))'' equivalente a
``(non Q) => (non P)''
Calcolo proposizionale e aritmetica ``modulo 2''
(un numero vale quanto il suo resto nella divisione per 2 in particolare x+x= 0, - x= x, x^2=x)
al posto di Vero mettiamo 1 (dispari) al posto di Falso 0 (pari), confondiamo ogni proposizione con il rispettivo valore di verita' assegnatole, si ha:
non P = P + 1 = 1 - P
P e Q = P Q
P o Q = P + Q +PQ = P + Q - PQ
P=>Q = P + 1 + PQ = - P +1 + PQ= - P +1 +Q -Q +PQ = (1-P) + Q - (1-P)Q =(non P ) o Q
ovvero le formule proposizionali con i connettivi si comportano come i polinomi a coefficienti 0 , 1
calcolati considerando il risultato 0 se vien pari , e il risultato 1 se vien dispari, ovvero
come polinomi a coefficienti 0, 1, -1 che calcolati danno solo 0 o 1 come risultati.
Calcolo proposizionale e operazioni insiemistiche
come gia' osservato se B={y in Y: P(y) e' vera} C={ y in Y : Q(y) e' vera}
B intersezione C = { y : P e Q }
B U C = { y : P o Q }
Y \ B = { y : non P }
Leggi di De Morgan per operazioni insiemistiche
Y \ (B intersezione C)= (Y\B) U (Y\C)
Y \ ( B U C) = (Y\B) intersezione (Y\C)
Leggi di De Morgan per connettivi proposizionali
non(P e Q ) = (non P) o (non Q)
non(P o Q ) = (non P) e (non Q)
-Algebra di insiemi:
Conviene mettere in risalto la struttura con le operazioni insiemistiche che riflette i connettivi logici fondamentali non , e , o:
un insieme M di sottoinsiemi di M si dice algebra se
A) tutto M sta in M
B) se A e B stanno in M allora anche : unione, intersezione e differenza stanno in M
In altre parole e' uno pseudoanello che ha come elemento anche tutto l'insieme ambiente M.
-Predicati e quantificatori
Notazioni di ``per ogni'' (A capovolta) e di ``esiste'' (E riflessa)
per ogni x( se x in A allora q(x)) in forma abbreviata per ogni x in A q(x)
esiste x( x in A e q(x)) in forma abbreviata esiste x in A : q(x)
Unioni ed intersezioni arbitrarie
Dato un iniseme di insiemi A l'insieme
Intersezione_ A = {y : per ogni a elemento di A y e' elemento di a}
si dice intersezione su A
i cui soli elementi sono quelli che sono elementi di tutti gli elementi di A
se per esempio A={Ai : i in I} l'intersezione e'
Intersezionei in I Ai ={y: per ogni i in I y e' elemento di Ai}
Dato un insieme di insiemi A vi e' l'insieme unione su A
che ha come soli elementi gli elementi di elementi di A:
U_A = {y : esiste a elemento di A per cui y e' elemento di a}
se per esempio A={Ai : i in I} l'unione e'
Ui in I Ai ={y: esiste i in I e y e' elemento di Ai}
Nel caso in cui A e' finito per esmpio A={A_1, A_2} , A_1=B e A_2 = C
U_A = Ui in {1,2} Ai = B U C e Intersezione_ A= Intersezionei in {1,2} Ai = B intersezione C
quantificatori ed operazioni insiemistiche
{y: per ogni x in X si ha P(x, y) } = Intersezionex in X { y : P(x,y)}
{y: esiste x in X per cui P(x,y) } = Ux in X { y : P(x,y)}
Leggi di De Morgan per unioni e intersezioni arbitrarie
Y\ Intersezionei in I Ai = Ui in I ( Y\Ai )
Y\ Ui in I Ai = Intersezionei in I (Y \Ai )
Leggi di De Morgan per i quantificatori
non (per ogni x P(x)) = esiste x (non P(x))
non (esiste x P(x)) = per ogni x (non P(x))
- Probabilita' prime considerazioni astratte
Si e' considerato a livello intuitivo la probabilita' come rapporto tre numero di casi favorevoli su numero di casi possibili. In tal caso la probabilita' risulta essere quello che si era chiamato una misura finitamente additiva. Una misura per cui la misura di tutte le possibilita' deve essere 1.
In astratto su un insieme X, detto spazio degli eventi elementari, (in molti casi sconosciuto ) i cui elementi si dicono appunto eventi elementari, si dice che
una probabilita' e' una misura matematica su X con valore ``del tutto'' eguale ad 1.
Alcuni sottoinsiemi di X saranno gli eventi (composti) di cui si vuole valutare la probabilita',
costituiscono l'algebra degli eventi per cui si calcola la probabilita'.
In quasi tutti i casi quello che conta e' come si fanno i calcoli con la probabilita' , non tanto X o l'algebra (dovendo essere suo elemento X) degli eventi di interesse.
Di questa basta quasi sempre sapere quali sono solo alcuni tra
suoi elementi e il loro valore di probabilita': la cosa di interesse e' quindi riuscire a calcolare la probabilita' degli eventi ottenuti da questi usando le operazioni insiemisiche (corrisponednti a quelle logiche non, e, o).
In particolare se A e B sono sottoinsiemi di X disgiunti P(A U B)= P(A) + P(B)
ovvero se R e Q sono eventualita' che si escludono P({ R o Q} ) = P({ x per cui R}) + P({x per cui Q})
definizione di eventi indipendenti: P(A intersecato B) = P(A) P(B)
ovvero R e Q sono eventulita' indipendenti se P({R e Q})= P({x: R}) P({x: Q})
Schema successo-insuccesso di Bernoulli
se il successo ha probabilita' p e l'insuccesso probabilita' q (quindi q=1 -p)
Distribuzione (o legge) binomiale di (esattamente) k succesi su n tentativi indipendenti:
P( di k successi su n tentativi (indipendenti)) =
[visto che non dipende dall'ordine dei diversi tentativi]
= fattore binomiale n su k P(nei primi k tentativi successo e negli ultimi n-k insuccesso)=
= fattore binomiale n su k P(successo primo tentativo e ... e insuccesso (k+1)-esimo tentativo e ...)=
[e' l'intersezione di n eventualita' indipendenti per ipotesi]
= fattore binomiale n su k P(successo primo tentativo) P ... P(insuccesso (k+1)-esimo tentativo) P... =
[i successi hanno probabilita' p gli insuccessi 1-p]
= fattore binomiale n su k p^k (1-p)^(n-k)
26-10-09 esercitazione 10 (ore 1 e 15 min.)
esercizi 6-10 test di ingresso ``matematica e problemi''
- Date tre proposizioni P, Q, R si sa che se Q e' vera ed R falsa allora P e' vera.
Se P e' falsa cosa si puo' dedurre? [Q falsa o R vera; R vera; Q falsa e R vera; Q ed R false]
- Si lancia una moneta non truccata quattro volte. Con che probabilita' esce testa almeno tre volte?
[5/16; 1/8; 1/4; 9/16]
-Su tre specie di pasci A, B, C, in un anno il rapporto tra numero di A e numero di B e' aumentato del 50%.
Quello tra numero di B e numero di C del 20%. Di quanto e' aumentato il rapporto tra numero di A e numero di C? [ 35%; 70%; 80%; 100%]
-Nel piano cartesiano si considera la semicirconferenza sopra la retta y=-2 di raggio 1 e centro (1,-2).
Di quali delle seguenti funzioni e' grafico?
[f(x)= 2 -radq(2x - x^2); radq(4x - x^2 - 3) -1; 1 - radq( 4x - x^2 -3); radq(2x - x^2) -2]
-Due angoli di un triangolo son eguali ad A con sen A= 0.8.Allora il seno del terzo angolo e':
[0.48; 0.64; 0.72; 0.96]
27-10-09 lezione 11 ( 30 min.) Ripetizione delle prime considerazioni astratte sul calcolo delle probabilita'.
27-10-09 esercitazione 11 (ore 1 e 30 min.)
esercizi 18- 20 test di ingresso ``linguaggio matematico di base, modellizzazione, ragionamento''
esercizi 11-15 test di ingresso `` matematica e problemi''
i testi sono reperibili nel sito http://www.testingressoscienze.org .
NOTA: nella lezione 6 del 13-10 invece del termine semianello si usa correntemente tra i matematici il termine pseudoanello, analogamente nella lezione 10 di ieri 26-10 invece che il termine anello si usa il termine algebra.
Si e' provveduto a mettere in risalto la definizione di algebra di insiemi per rilevanza del collegamento tra le operazioni insiemistiche e i connettivi logici non, e , o.
29-10-09 lezione 12 (ore 2)
Riferimenti:[EB] (coordinate polari) cap. 5 pagg 114- 115, 119-129, 140-142, cap. 6 pagg. 162-165, 169;
[EB] cap . 14 pagg. 509-511 esempio 14.5.7; [MA1] (coordinate polari) cap. 5 pagg. 266-268;
[BDM] (polari e sferiche) cap.2 pagg. 79-81; [IRS] (polari) cap. 5 pagg.179-180; [VV] pag. 87
Riferimenti numeri complessi:
[EB] cap.15 pagg.547-558; [MA1] cap. 9 pagg. 505-506 curiosita' 9.6;
[BDM] cap.1 pagg.40-42, pag. 54, cap.6 pagg.252-253, ;
[IRS] cap 5.6 pagg.180-183.
Coordinate affini: come gia' piu' volte osservato dati due vettori u e v non paralleli nel piano con origine, per ogni punto P vi sono solo due numeri reali a eb P=a u+bv : costruzione geometrica corrispondente: per il punto P si tracciano le due parellele a v e u le loro intersezioni con tu , t in R e rispettivamente con tv , t in R son i punti
au rispettivamente bv
Coordinate polari nel piano e arcotangente:
intersezione tra semirette dall'origine e circonferenze ivi centrate:
P=(r cos t, r sin t) = (x, y), x=r cos t , y= r sin t
r distanza dall'origine r= radq( x^2 +y^2 )
t misura in radianti dell'angolo in [0; 2 pig [ ``percorso in senso antiorario'' dalla semiretta dell'asse orizzontale {(x,0): x >o= 0} alla semiretta dall'origine al punto dato,
ovvero l'arco tra 0 e 2 pig la cui tangente e' la pendenza, nel sistema di coordinate cartesiano , della semiretta dall'origine al punto P
t =arctan y/x se x > 0 e y >o= 0 primo quadrante senza semiretta coordinate verticale positiva
t= pig/2 se x = 0 e y >o= 0 semiretta verticale positiva
t =pig + arctan y/x se x < 0 secondo e terzo quadrante senza semiratta verticale negativa
t=3/2 pig se x = 0 e y<o= 0 semiretta verticale negativa
t= 2pig + arctan y/x se x > 0 e y<o= 0 quarto quadrante senza semiretta verticale negativa e senza semiretta orizzontale positiva
quindi il piano cartesiano privato dell'origine si rappresenta in coordinate polari con ``la striscia''
{(r, t) : r>0 e 0 =o< t < 2 pig } = ]0; +oo[ x [0; 2pig [
per definizione la seconda coordinata polare e' sempre non negativa e strettamente minore di 2 pig
L' arcotangente di un numero reale d e' per definizione compresa tra - pig /2 e pig /2
e' la misura in radianti dell'unico arco in questo intervallo che ha tangente eguale a d .
spirale di Archimede
spirale logaritmica
Coordinate cilindriche nello spazio: intersezione di un piano orizzontale con un semipiano verticale contenente l'asse verticale e con un cilindro circolare con asse quello verticale
P= ( r cos t , r sin t , z) x = r cos t , y = r sin t , z=z
r>0 , t in [0, 2pig[ , z in R .
r= radq (x^2 +y^2) = distanza di P dall'asse verticale
t coordinate polare angolare della proiezione ortogonale di P sul piano delle prime due coordinate
z quota di P sull'asse verticale
si descrive in modo univoco R^3 \ {(0,0, z); z in R}
doppi coni di rotazione come luoghi di zeri
Coordinate sferiche nello spazio tridimensionale: intersezione di una semiretta con una sfera, ovvero intersezione di una sfera con un semipiano verticale contenente l'asse verticale e con un piano orizzontale,
P= (R sin s cos t, R sin s sin t , R cos s) x = R sin s cos t , y = R sin s sin t , z= R cos s
R>0 , t in [0; 2 pig [ , -pig < s < pig
R= radq( x^2+ y^2 + z^2) = distanza di P dall'origine
s misura in radianti tra il semiasse verticale positivo e la semiretta dall'origine a P
(latitudine)
t coordinata polare angolare della proiezione ortogonale di P sul piano delle prime due coordinate
(longitudine a meno di un angolo piatto)
R sin s=r coordinata polare radiale della proiezione ortogonale di P sul piano delle prime due coordinate
si descrive in modo univoco lo spazio cartesiano tridimensionale meno l'asse verticale
Numeri complessi.
ALTRI APPUNTI SU NUMERI COMPLESSI
Tra i numeri reali l'equazione x^2=-1 non ha soluzioni, essendo i quadrati di un numero non negativi.
La si aggiunge e la si chiama i: i^2= -1 e si opera normalmente con le operazioni tenendo presente questa identita' per ridurre a 0 o a 1gli esponenenti di i;
in altri termini:
si considerano i polinomi a coefficienti reali in una variabile che si denota usualmente con i, R[i] si opera normalmente con essi con moltiplicazione e addizione di polinomi, e si riduce il risultato a un binomio di primo grado usando la relazione i^2=-1.
Quindi i numeri complessi sono la struttura, indicata con C, dei binomi di primo grado in una variabile i a coefficienti reali, con la regola di calcolo aggiuntiva i^2+1=0
Chiaramente a in R si identifica con a +i0.
Per i numeri complessi si sono introdotte le nozioni:
- somma e prodotto di numeri complessi
(quelle dei polinomi con la regola cha al posto di i^2 si mette -1)
formula per il prodotto (a+ib)(x+iy)= ax-by + (ay+bx)i
- parte reale di z il termine noto: indicato con Re z
- parte immaginaria il coefficiente reale del termine di primo grado: indicato con Im z
ovviamente z = Re z + i Im z
- inverso z^{-1}di un numero complesso z non nullo, e relativo calcolo
- coniugato ``z sopralineato'' = x- i y di un numero complesso z= x+i y
- modulo |z| di un numero complesso z
ottenendo 1/z = (coniugato z) /|z|^2 , |zw|=|z||w| , con(zw)=con(z)con(w), con(z+w)=con(z) +con(w)
quindi un numero complesso z e' in R se e solo se z= coniugato(z)
Si sono messe in rilievo le prime proprieta' geometriche dei numeri complessi
identificandoli con le coppie di numeri reali (a,b) = a +i b
si ribadisce che, come le cordinate cartesiane, due numeri complessi sono eguali se e solo se
hanno la stessa parte reale e la stessa parte immaginaria
e.g. 1/(3+i) = a +i b deve essere (a+ib) (3+i)=1 svolgendo il primo termine dell'equazione
deve essere 3a- b + (3b +a)i =1 = 1 +0 i e quindi
deve essere 3a-b =1 e 3b+a =0
e quindi risolvendo il sistema 1/(3+i) = 3/radq(10) - i/radq (10)
- la somma corrisponde alla traslazione
- il coniugato corrisponde al riflesso rispetto all'asse ``reale'' delle ascisse
- il modulo alla distanza dall'origine
- coordinate polari e numeri complessi
z=r( cos t + i sin t) quindi z^2 = r^2 (cos 2t + i sin 2t)
si nota |z|=r e che t differisce per la coordinata polare eventualmente di un multiplo di 2pig
- piu' in generale se z=r( cos t + i sin t) e w = R(cos s + i sin s) allora dalle formule di addizione
si ha
zw = rR( cos (s+t) + i sin (s+t) )
ove s+t eventualmente differisce per un multplo di 2 pig dalla coordinata angolare polare di zw.
quindi la coordinata angolare polare di un prodotto
e' la somma (a meno di multipli di 2 pig) delle coordinate angolari dei due fattori
le coordinate angolari si comportano come degli esponenti.
- quindi il prodotto per un prefissato numero complesso w di un altro numero complesso z
corrisponde a
i- ruotare ``in senso antiorario'' z attorno all'origine di un angolo pari alla coordinata angolare di w
ii- quindi dilatare con centro l'origine di un fattore |w| (coordinata polare radiale di w)
Forma esponenziale di un numero complesso
se si scrive |z| = e^p (e costante di Nepero di cui si parlera' in seguito per ora basta che e >1)
allora z= e^p (cos t + i sin t)
si osserva che i numeri complessi cos t + i sin t sono di modulo 1, descrivono la circonferenza unitaria di centro l'origine
vista la proprieta' delle coordinate angolari si definisce
e^{i t } = cos t + i sin t
e quindi per ogni numero complesso u si ha l'esponenziale complesso
e^u = e^{Re u} e^{i Im u}
si osserva quindi che
coordinata radiale di e ^u = |e^u| = e ^{Re u}
coordinata angolare polare di e^u = Im u + 2k pig per qualche k in Z
Il fatto notevole e' che aggiungendo ai numeri reali le radici di z^2=-1, cioe' i e -i, si recuperano tutte le radici di ogni polinomio: e' il
TEOREMA fondamentale dell'algebra
ogni polinomio a coefficienti complessi di grado n ha esattamente n radici complesse contate con molteplicita'
ovvero se P(z)= a_0 +a_1 z + ... +a_n z^n, con a_n non 0 , e i coefficienti complessi
allora P(z) = a_n prodotti di (z-c)^k
ove la somma dei k e' n, e c sono i numeri complessi per cui P(c)=0.
In particolare un polinomio a coefficienti reali se ha una radice complessa ha anche la coniugata di questa come radice e con la stessa molteplicita'.
ESERCIZI lasciati
trovare data la forma polare di un numero complesso le sue radici terze sempre in forma polare.
2-11-09 lezione 13 (ore 1)
Riferimenti:
[EB] cap.15 pagg.559-560, 569-570;
[IRS] cap 5.6 pagg.184-185.
Riassunto della precedente lezione
Altre relazioni elementari interessanti tra numeri complessi
1/i = - i = i^3
i^n e' periodico di periodo 4 : i^0 = 1, i^1=i, i^2 =- 1 , i^3 = - i
z+ con(z) = 2 Re z, z - con (z) = 2 i Im z
cos a = 1/2( e^{ia} + e^{-ia}) , sin a = - i/2 ( e^{ia}- e^{-ia})
con (e^z) = e^{con z}
Definizioni:
Argomento principale di un numero complesso z non nullo
l'unico numero a in [0; 2 pig[ per cui z=|z| (cos a + i sin a)
Argomento naturale di un numero complesso z non nullo
l'unico numero a in ]- pig; pig] per cui z=|z| (cos a + i sin a)
Quindi vale la relazione: Arg(zw) = Arg z + Arg w + 2 k pig per qualche k in Z.
Arcotangente di x : artan x = y
per definizione compreso strettamente tra - pig /2 e pig /2
dell'unico numero y in questo intervallo per cui tan y =x .
Arcoseno di x : arcsin x = y
per definizione compreso tra, eventualmente eguale, - pig /2 e pig /2
dell'unico numero y in questo intervallo per cui sin y =x .
Arcocoseno di x : arcos x = y
per definizione compreso tra, eventualmente eguale, 0 e pig
dell'unico numero y in questo intervallo per cui cos y =x .
Radici n-sime di un numero complesso:
si tratta di risolvere dato w l'equazione z^n= w
conviene scrivere il termine noto in forma polare w = r ( cos a + i sin a) con 0 <o= a < 2 pig
quindi l'incognita z = R (cos b + i sin b) con R e cos b e sin b da calcolare in termini delle quantita' note
r, cos a, sin a
per quanto visto z^n = R^n (cos nb + i sin nb)
considerando che:
- due numeri complessi sono eguali nel caso in cui
hanno lo stesso modulo e angoli che differiscono per un multiplo di 2 pig
- delle varie misure angolari che individuano le radici ennesime di w ci interessano
solo quelle tra 0 e 2 pig
dall'equazione iniziale z^n = w si ottiene il sistema
R^n = r
nb = a + 2 k pig per qualche k in Z ,
0 <o= b < 2 pig
quindi R= r^{1/n} , per poi risolvere il sistema nb = a + 2 k pig per k in Z e 0 <o= b < 2 pig
tra le infinite misure angolari b = a/n + 2 k/ n pig , k in Z ottenute dalle prime equazioni
si usa la diseguaglianza per determinare qualle diverse che individuano diversi numeri
poiche' si e' scelto a tra 0 e 2 pig anche
a/n e' tra 0 e 2 pig (k=0)
a/n + 2/n pig e' tra 0 e 2 pig (k=1)
.
.
.
a/n + 2(n-1)/n pig e' tra 0 e 2 pig (k= n-1)
prendendo k maggiori si ottengono gli stessi valori con aggiunto un multiplo di 2 pig e quindi si individua lo stesso numero complesso ( a/n + 2n/n pig = a/n + 2 pig (k=n), a/n 2 pig + pig/n (k=n+1) ... ).
Quindi le radici ennesime di w= r (cos a + i sin a) sono esattamente n:
z_1 = r^{1/n} ( cos a/ n + i sin a/n)
z_2 = r^{1/n} ( cos (a/ n + 2 pig/n) + i sin( a/n +2 pig/n))
.
.
.
z_{k+1} = r^{1/n} ( cos (a/ n + 2 k/n pig) + i sin( a/n +2 k/n pig))
.
.
.
z_n = r^{1/n} ( cos (a/ n + 2 (n-1)/n pig) + i sin( a/n +2 (n-1)/n pig )
se inoltre (come nel calcolo esposto) a e' in [0, 2 pig[ allora z_1 e' la radice ennesima di argomento principale minimo
NOTAZIONE: con la notazione della radice ennesima di un numero complesso spesso conviene denotare l'insieme delle sue n radici distinte.
Quindi piuttosto che scrivere z= w^{1/n}
si scrive z in w^{1/n}
Alcune volte invece (per esempio parlando della radice aritmetica di un numero reale) e' conveniente indicare con w^{1/n} la radice ennesima di argomento principale minimo.
Interpretazione geometrica delle radici complesse :
- le radici complesse ennesime di w corrispondono a punti sulla circonferenza di centro l'origine e raggio
|w|^{1/n}
-gli argomenti delle radici ennesime complesse ordinati differiscono uno dal successivo per 2/n pig
quindi le radici ennesime complesse di w
sono i vertici dell'ennagono regolare inscritto nella circonferenza di raggio |w|^{1/n}
a partire dal vertice di argomento principale minimo
OSSERVAZIONE: nella pratica volendo le radici complesse nella forma x + i y (se non si vogliono fare calcoli approssimati per ricavare dal termine noto w dato come u + i v il suo argomento principale a) conviene ricavare x = r^{1/n} cos a/n e y = r^{1/n} cos a/n della radice di argomento minimo:
usando le relazioni trigonometriche al contrario si ricavano relazioni del tipo
u/|w| = cos a = cos (n a/n) = cos a/n cos ( a (n-1) /n) - sin a/n sin ( a (n-1)/n) = ....
espressione solo con cos e sin a/n
v/|w| = sin a = sin ( n a/n) = sin a/ n cos (a(n-1)/n) + cos a/n sin (a (n-1)/n) = .....
espressione solo con cos e sin a/n
quindi un sistema con incognite ( cos a/n , sin a/ n ) di cui serve trovare solo le soluzioni di argomento minimo (in particolare maggiori di 0 e minori di 2 pig/ n se a era l'argomento principale di w)
ovvero sin a/n tra 0 e sin 2pig /n e cos a/n tra cos 2 pig/n e 1.
Le altre radici si ricavano usando in modo diretto le formule di addizione, poiche' le radici ``successive'' hanno argomenti che differiscono di 2 pig/n.
Questo approccio e' comodo quando: n non e' molto grande, o n e' una potenza di 2.
Radici quadrate di un numero complesso
basta trovare la radice di argomento minimo z_1
l'altra sara' -z_1
Radici di trinomi di secondo grado:
per trovare le soluzioni complesse u e v di Az^2 +B z + C= 0 , dati A, B, C in C
vale la solita formula
{ u, v}= 1/(2A) ( - B + radq( B^2- 4AC)) (eguaglianza di insiemi se con radq
si intende l'insieme di tutte le radici quadrate)
oppure
{ u,v} = 1/(2A)( - B + o - radq( B^2- 4AC)) ( se, come quando B^2-4AC e' reale non negativo, con radq
si intende la radice di argomento minimo)
In particolare, con quest'ultima convenzione, il caso B^2 -4AC reale negativo si ha la scrittura piu' suggestiva
{u, v} = 1/(2A)( - B + o - i radq|B^2- 4AC |)
Fattorizzazione di polinomi a coefficienti reali:
si ricorda il
TEOREMA fondamentale dell'algebra
ogni polinomio a coefficienti complessi di grado n ha esattamente n radici complesse contate con molteplicita'
ovvero se P(z)= a_0 +a_1 z + ... +a_n z^n, con a_n non 0 , e i coefficienti complessi
allora P(z) = a_n prodotti di (z-c)^k
ove la somma dei k e' n,
e c sono i numeri complessi per cui P(c)=0.
Ora se i coefficienti del polinomio P sono tutti reali si osserva che
-se c = a + ib e radice di P anche con (c) = a-i b e' radice di P
infatti
P(c) = 0= con(0) = con(P(c)) =
poiche' i coniugati di somma e prodotto sono rispettivamente la somma e il prodotto dei coniugati e coniugato di ogni coefficiente e' eguale al coefficiente stesso perche' e' reale
= P(con(c))
- se si esegue il prodotto (z-c)(z- con(c))= (z- (a+i b))(a-(a-ib)) = ((z-a) - ib ) ((z-a) +i b)
usando la formula della diffrenza di due quadrati si ottiene
(z-a)^2 - (i b)^2 = (z-a)^2 +b^2
Quindi ogni polinomio P, di grado n con coefficiente di grado massimo a_n non nullo, a coefficienti reali si scrive
P(x) = a_n prodotto di termini del tipo (x- r)^h prodotto di termini del tipo ((x-a)^2 +b^2) ^k
ove
r sono le radici reali
a+ib e a-ib sono le radici non reali (b diverso da 0)
e la somma degli h e dei 2k e' eguale ad n.
.2-11-09 esercitazione 12 (ore 1)
- Calcolare in forma cartesiana le radici quadrate di 3+2i
- trovare gli zeri (complessi) di un trinomio di secondo grado a coefficienti complessi.
- Fattorizzare con polinomi a coefficienti reali non ulteriormente scomponibili x^4 +1
- Fattorizzare con polinomi a coefficienti reali non ulteriormente scomponibili x^8+1
3-11-09 lezione 14 (ore 1)
Riferimenti (relativi ai nuovi argomenti introdotti): [EB] cap. 8 pag 213, cap. 14 (non vi e' interpretazione geometrica del determinante) pagg. 511, 515-516, [MA1] cap. 5 pag. 281, Esempio 5.31, pag. 283 Esempio 5.32, cap. 10.8 pagg. 579-580, 583 (tabella) , [BDM] cap.7 Esempio 7.33 pagg.279-280, cap. 3.4 pagg. 124 , 129-129, [IRS] cap. 3.3.1 pagg.123-124, cap. 5 (no int.geo.) pag. 201 ,[VV] cap. 3 pagg. 38-45, cap. 4 (non vi e' interpretazione geometrica) pag. 72.
Ripetizione di alcuni temi affrontati nella precedente lezione:
- l'argomento di un prodotto di numeri complessi e' la somma a meno di multipli di 2 pig degli argomenti dei fattori;
- radici ennesime di un numero complesso ed interpretazione geometrica;
- teorema fondamentale dell'algebra e fattorizzazione di polinomi a coefficienti reali:
i trinomi di secondo grado a coefficienti reali con discriminante negativo sono somma del quadrato di un binomio di primo grado e di un numero positivo.
Differenza di potenze
A^2-B^2= (A-B)(A+B)
A^3-B^3=(A-B)(A^2 + AB+B^2)
A^4-B^4=(A^2-B^2)(A^2+B^2)=(A-B)(A+B)(A^2+B^2)=(A-B)(A^3+ A^2B +AB^2 +B^3)
Piu' in general si ottiene per ogni esponente naturale n
A^n -B^n = (A-B)( A^(n-1) + A^(n-2) B + ...+ AB^(n-2) +B^(n-1))
si osserva che ogni addendo del secondo membro ha somma degli esponenti eguali ad n-1
infatti
(A-B)( A^(n-1) + A^(n-2) B + ...+ AB^(n-2) +B^(n-1))=
= A ( A^(n-1) + A^(n-2) B + ...+ AB^(n-2) +B^(n-1))
- B ( A^(n-1) + A^(n-2) B + ...+ AB^(n-2) +B^(n-1)) =
= A^n + A^(n-1) B + A^(n-2) B^2 + ... + A^2B^(n-2) +AB^(n-1)
- B A^(n-1) - A^(n-2) B^2 - ... - AB^(n-1) - B^n
Nel caso in cui n=2m+1 e' dispari se al posto di B si mette -B si ottiene:
A^n + B^n = (A + B)( A^(n-1) - A^(n-2) B + ... - AB^(n-2) +B^(n-1))
gli addendi del secondo fattore son a segni alterni avendo il meno le potenze dispari di -B
Per A=1 si ottiene un fattore che e' la somma delle potenze crescenti da 0 a n-1 di B
1-B^n=(1-B)(1+B+...+B^(n-1)), il secondo fattore si chiama polinomio ciclotomico (quando n e' un numero primo).
Determinante di matrici due righe e due colonne:
significato geometrico, caratterizzazione algebrica, legame con il prodotto di numeri complessi
z= a + i b, w= A + i B , con(w)= A - i B
per calcolare l'area P del parallelogramma di vertici 0, z, w e z+w usando il teorema dei seni si ha
P= |z||w| |sin w0z |
ma l'angolo da w a z (orientato ovvero con segno) w0z = Arg z - Arg w= Arg z+ Arg (con(w))
quindi tale area e' il modulo dalla parte immaginaria del seguente prodotto
z con(w) = |z||w| cos (Arg z+ Arg con (w)) + i |z||w| sin (Arg z + Arg con(w))
= |z||w| cos (Arg z - Arg w) + i |z||w| sin (Arg z - Arg w)
= |z||w| cos (w0z) + i |z||w| sin (w0z)
= aA + bB + i ( Ab -Ba)
Definizione: det ((A,B)(a,b)) = Ab-aB determinante della matrice di prima colonna (A,B) e seconda (a,b)
= (A,B). (a,b) + i det( (A,B), (a,b))
Il determinante di una matrice permette di esprimere due cose:
-il suo segno l'orientazione (relativamente al sistema di coordinate cartesiano)
-il suo modulo l'area del parallelogramma di vertici l'origine, i punti che hanno come coordinate le colonne e la loro somma:
Area parallelogramma di vertici (0,0), v, w, v+w = | det (v, w)| = |v||w|radq( 1- [v .w /(|v||w|)]^2)
in particolare permette un'espressione diretta del seno cosi come il prodotto scalare permetteva quella del coseno:
v.w det (v, w )
cos vow = ---------------- sin vow = ----------------
|v| |w| |v| |w|
se v=(a,b), w=(A,B)
|v||w| cos vow = aA+ bB |v||w| sin vow = aB - bA
Definizione orientazione relativa al riferimento cartesiano in R^2:
due vettori u e v ordinati in coppia ordinata (u,v) si dicono
avere la stessa orientazione dei vettori coordinati cartesiani in coppia ordinata ((1,0),(0,1))
ovvero avere orientazione positiva
se det(u,v) >0
si dicono avere orientazione negativa
se det(u,v) <0
Definizione orientazione relativa (equiorientazione):
due coppie di vettori ordinate (u,v) e (P, Q) hanno la stessa orientazione ovvero sono equiorientate
se det(u,v) e det(P,Q) hanno lo stesso segno non nullo
cioe'
det(u,v) det(P,q) >0
OSSERVAZIONE: l'orientazione e' un concetto relativo come quello di percentuale.
Proprieta' algebriche del determinante che lo caratterizzano:
Piuttosto che dedurre algebricamente le proprieta' algebriche (il che e' tutto sommato somma-mente noioso) si deducono dall'interpretazione geometrica come area orientata:
a livello intuitiuvo l'area orientata A(v,w) di un parallelogramma di vertici (0,0), v, w e v+w soddisfa
1) A(v,w) = -A(w,v) (definizione di area orientata),
2) A(tv, w) = tA(v,w) per t in R (vedere prima figura: se una sola dimensione aumenta di un
fattore cosi l'area)
3) A(v+tw, w) = A(v,w) per t in R (vedere seconda figura: i parallelogrammi O,v,w, v+w e O, v+tw,w,
v+tw+w hanno stesse base ed altezza)
4) A((1,0), (0,1)) = 1 (l'area di un quadrato di lato unitario orientato con prima base quella orizzontale)
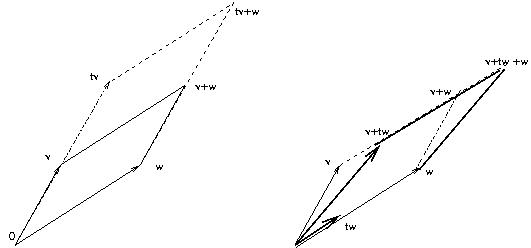
- Da 1), 2), 3) segue
3 bis) A(v+V,w) = A(v,w) +A(V,w)
(infatti: se v e w sono paralleli v=sw e quindi da 3) A(sw+V,w)= A(V,w) = sA(w,w)+ A(V,w) da 1); se invece v e w non lo sono ogni V=sv +tw e si usano 3) 2) da sinistra a destra e poi da destra a sinistra)
- TEOREMA 1 sul determinante:
Vi e' un solo modo di associare ad una matrice M n per n un numero A(M) in modo che
1) se N e' ottenuta da M scambiando di posto due colonne: A(M) = - A(N) (alternante)
2) se N e' ottenuta da M moltiplicando una colonna per t in R: A(N) = t A(M)
3bis) A(M^1 +V, M^2 ... ) = A(M) + A(V, M^2, ... ) (multilineare)
4) se M e' fatta con 1 sulla diagonale discendente e 0 altrove : A(M)= 1
- TEOREMA 1 bis sul determinante: sviluppo per colonne del determinante
Nel caso due colonne per due coordinate si procede come segue
A((p,q),(h,k))=
A( p(1,0) + q(0,1), (h, k))=
[3 bis) e 2)]
pA((1,0), (h,k)) +qA((0,1), (h,k)) =
pA((1,0), h(1,0)+ k(0,1)) +qA((0,1), h(1,0)+ k(0,1)) =
[su ogni addendo1), 2), 3 bis) e ancora1)]
phA((1,0),(1,0)) + pkA((1,0),(0,1)) + qhA((0,1),(1,0)) + qkA((0,1),(0,1)) =
[per 1 A(v,v)=0]
pkA((1,0),(0,1)) + qhA((0,1),(1,0)) =
[1)]
(pk - qh)A((1,0),(0,1))=
[4)]
pk - qh.
e quindi si ottiene proprio il determinante!
Mettiamo in risalto una proprieta' che e' utile in piu' dimensioni.
Ora se due punti sono allineati con l'origine nel piano, ovvero due vettori sono paralleli, il parallelogramma da essi generato e' un segmento di area nulla: quindi due vettori sono paralleli se e solo se il determinante della matrice che ha come colonne le loro coordinate e' nullo:
TEOREMA
v(a,b) e w(A,B) in R^2 sono paralleli se e solo se sv + tw = O per qualche s e t in R non entrambi nulli
se e solo se
det(v,w)=0, cioe' aB=Ab
.3-11-09 esercitazione 13 (ore 1)
- calcolare le soluzioni u complesse di 2u +6/u =5
e' equivalente a 2u^2 -5u +6=0 e u non 0
le soluzioni sono
1/4( 5 +o- i radq(23)) giustamente complesse e coniugate.
- non necessita' in molti casi del calcolo dell'argomento principale a di w, dato in forma cartesiana u+ i v, per ricavarne le radici ennesime:
basta infatti determinare
cos a/n e sin a/n in funzione di cos a = u/rad(u^2+v^2) e sin a =v/rad(u^2+v^2) noti
usando ``all'indietro'' le relazioni
cos a = cos (n (a/n)) = cos((n-1) a/n ) cos a/n - sin ((n-1) a/n ) sin a/n = ...
sin a = sin (n (a/n)) = sin ((n-1) a/n ) cos a/n + sin ((n-1) a/n ) cos a/n = ...
- calcolare le soluzioni
(2 + i)u^2 -5 u+ 6=0
si usa la solita formula 1/2A( -B +o- radq(B^2 - 4AC))
ove A=2+i, B= -5 , C=6, radq e' la radice quadrata di argomento principale minimo
1/(2A)= (2-i)/10
radq(B^2 - 4AC) =radq(- 23 - 24 i)
il modulo r delle radici quadrate di -23 -24 i e' (23^2 +24^2)^(1/4)
per calcolare le coordinate delle radici bisogna calcolare cos a/2 e sin a/2
nel caso non si calcola direttamente l'argomento a del numero complesso -23 -24 i in forma cartesiana
ma il suo coseno e il suo seno
cos a = cos Arg(-23 - 24i) = - 23/radq(23^2+24^2)
sin a = sin Arg(-23-24i ) = - 24/radq(23^2+24^2)
quindi come osservato in generale
- 23/radq(23^2+24^2) = 2 [cos (a/2)]^2 -1 per cui
[cos (a/2)]^2 = 1/2(1- 23/radq(23^2+24^2) )
[sin (a/2)]^2 = 1- [cos (a/2)]^2 = 1/2(1+23/radq(23^2+24^2))
ora per sapere che segno hanno rcos (a/2) e rsin (a/2), considerando che sono le coordinate della radice di argomento minimo poiche' -23- i24 sta nel terzo quadrante il suo argomento principale a deve essere tra pig e 3/2 pig, quindi a/2 tra pig/2 e 3pig /4 cioe' nel secondo quadrante:
quindi il suo
coseno dev'essere negativo
mentre il seno positivo (questo sempre per il seno dell'argomento minimo di una radice quadrata!)
per cui
radq(-23-24 i)=
(23^2 +24^2)^(1/4) {- radq[1/2(1- 23/radq(23^2+24^2) )] + i radq[1/2(1- 23/radq(23^2+24^2) )] }
da cui si ricavano le agognate soluzioni.
- fattorizzare x^4+1
- fattorizzare x^9+1 (non ultimato)
5-11-09 lezione 15 (ore 1 e 30 minuti)
Riferimenti : [MA1] cap. 10.8 pagg. 580-583 , [BDM] cap. 3.4 pagg. 125-129.
-Un segmento tra due punti P e Q puo' essere descritto come insieme dei punti del tipo
P+ t(Q-P) per qualche t in [0,1],
ovvero come cammino di velocita' costane Q-P, dal tempo t=0 in P sino al tempo t=1.
Definizione di sottoinsieme convesso di R^n
un sottoinsieme C e' convesso se contiene i segmenti interi con estremi suoi elementi
ovvero
se i punti P e Q sono in C allora per ogni t in [0,1] il punto (1-t)P+ tQ e' in C
Come visto nella precedente lezioni quattro semplici proprieta' che intuitivamente deve soddisfare la nozione di ``area orientata '' ne permettono il calcolo con le coordinate delle colonne, cio' e' vero per la nozione intuitiva di n-volume orientato:
- TEOREMA 1 sul determinante:
Vi e' un solo modo di associare ad una matrice M n per n un numero A(M) in modo che
1) se N e' ottenuta da M scambiando di posto due colonne: A(M) = - A(N) (alternante)
2) se N e' ottenuta da M moltiplicando una colonna per t in R: A(N) = t A(M)
3bis) A(M^1 +V, M^2 ... ) = A(M) + A(V, M^2, ... ) (multilineare)
4) se M e' fatta con 1 sulla diagonale discendente e 0 altrove : A(M)= 1
Definizione: si definisce cosi il determinante di M: A(M) = det M
NOTA: il pararelleo intuitivo tra determiante ed area o volume orientato non e' perfetto, sarebbe meglio pensare il determinante come rapporto di arre.
Definizione orientazione relativa al riferimento cartesiano in R^n:
Si dice che n vettori ordinati hanno la stessa orientazione dei vettori coordinati cartesiani, ordinati come uso, ovvero avere orientazione positiva se il determinante della matrice che li come colonne e' > 0.
Si dice che hanno orientazione negativa se il determinante della matrice che li come colonne e' < 0.
Definizione orientazione relativa (equiorientazione):
Due n-ple ordinate di vettori hanno la stessa orientazione se il prodotto dei determinanti delle due matrici che rispettivamente li hanno come colonne e' strettamente maggiore di zero.
-TEOREMA 1 bis sul determinante:
sviluppo rispetto alla k-esima colonna del determinante di M=(M_i^j), i e j tra 1 ed n
det M = somma per i tra 1 ed n di (-1)^{i+k} M_i^k det(sottomatrice ottenuta cancellando la riga i e la colonna k)
permette di calcolare il determinante di una matrice n righe e n colonne calcolando determinanti di matrici n-1 righe ed n-1 colonne
Riassumendo
det matrice di prima colonna (a,b) e seconda (A, B)= aB-bA
det matrice di prima colonna (a,b,c) seconda (p,q,r) e terza (A,B,C)=
a(qC-Br) - b(pC -Ar) + c(pB-Aq)
det matrice di colonne M^1 ... M^n =(sviluppo rispetto alla prima colonna)
M^1_1 det (della matrice senza la prima colonna e la prima riga) +
- M^1_2 det (della matrice senza la prima colonna e la seconda riga) +
...
(-1)^(1+i) M^1_i det (della matrice senza la prima colonna e le i-esima riga) +
...
AGGIUNTA RISPETTO A QUANTO DETTO A LEZIONE:
Notazione: se s_1, .... s_n e' una permutazione di 1 ... n e si chiama N(s) il numero di scambi che ci vuole per riordinarla in modo crescente, si pone e(s)=(-1)^N(s) = segno dei prodotti di (s_j - s_i ) con i<j
-TEOREMA 1 ter sul determinante:
det M = somma al variare della permutazione s dei primi n numeri di e(s) M_s(1)^1 x... x M_s(n)^n
Definizione: se M e' una matrice con m righe ed n colonne M=(M_i^j) i tra 1 ed m, j tra 1 ed n
si dice trasposta di M indicata con t^M la matrice ottenuta da M
scambiando ordinatamente le righe con le colonne
t^M e' una matrice con n righe ed m colonne (t^M)_i^j =M_j^i, j tra 1 ed m, i tra 1 ed n
FINE AGGIUNTA
Dalla seconda formula per il detrminante si ottiene immediatamente
-TEOREMA 2 sul determinante: det ( M ) = det ( t^M )
Considerando a livello intuitivo che il volume n dimensionale e' nullo per sottoinsiemi di dimensione minore e' ragionevole il seguente importante teorema
-TEOREMA 3 sul determinante:
det M = 0 se e solo se i vettori colonna sono in un iperpiano n-1 dimensionale passante per l'origine
se e solo se i vettori riga sono in un iperpiano n-1 dimensionale passante per l'origine
nel caso di tre vettori u=(a,b,c,), v=(p,q,r), w=(A,B,C) in R^3 se M e' la matrice con colonne le loro coordinate M= (u,v, w)
det M = 0
se e solo se u, v, w sono complanari con O
se e solo se uno dei tre vettori e' congiunto all'origine con una spezzata a lati paralleli agli altri due
se e solo se uno dei tre vettori e' somma di multipli degli altri due
se e solo se vi sono tre numeri x, y, z non tutti nulli per cui eu+f v,+g w = O
cioe' il sistema xa +yp +zA=0, xb+fyq+zB= 0 , xc+ yr+zC=0 ha una soluzione (x,y,z) non nulla.
Prodotto esterno o prodotto vettoriale in R^3 :
Definizione: se v=(p,q,r), w=(A,B,C) non sono paralleli si definisce v x w il vettore per cui:
- ortogonale al piano per l'origine, v e w,
- il sistema di coordinate (v x w , v , w ) e' con orientazione relativa positiva,
- il suo modulo e' eguale all'area del parallelogramma di vertici O, v, w, v + w
ovvero | v| | w| |sin v O w |
Altrimenti v x w =O.
***UN CALCOLO NON SVOLTO A LEZIONE
Troviamo le coordinate (x,y,z) di v x w a partire da quelle di v e w:
x p + yq + zr = 0
xA + yB + zC = 0 sono le condizioni di ortogonalita' da queste si otterranno infinite soluzioni tutta la
retta per l'origine ortogonale al piano per l'origine ove stanno v e w:
se p ed A son diversi da 0 si moltiplca la prima per A la seconda per p e si sottraggono
(se A o p son nulli le si moltiplica ripettivamente per B e q o per C e r e almeno una di queste coppie e' di numeri non nulli oppure v e w son paralleli)
yqA +z rA- yBp - zCp =z(rA-Cp) - y(pB-qA) =0 cioe' z(rA-Cp) = y(pB-qA)
si moltiplica la prima equazione per pB-qA o per rA-Cp e si sostituisce
xp(pB-qA) + z(rA-Cp)q +zr(pB-qA)= xp(pB-qA) - zp(Cq - rB)=0 cioe' x(pB-qA) = z (Cq - rB)
quindi i vettori del tipo t (Cq - rB, rA-Cp,pB-qA) soddisfano tutti queste relazioni.
Poiche' det (v x w , v , w ) = x(qC-Br) - y(pC -Ar) + z(pB-Aq) >0 visto che
x=t (Cq - rB)
y= t (rA-Cp)
z=t (pB-qA)
0< det (v x w , v , w )= t[ (qC-Br)^2+ (pC -Ar)^2+(pB-Aq)^2]: quindi vanno considerati solo i t >0.
Per trovare il t giusto si deve imporre | t (Cq - rB, rA-Cp,pB-qA)|= | v| | w| |sin v O w |
una via conveniente e' usare la seguente formula
*** RIPRESA LEZIONE
Formula di Cauchy-Crofton-Pitagora
- L'area di un parallelogramma e' eguale alla radice quadrata della somma dei quadrati delle arree dei parallelogrammi ottenuti proiettandolo ortogonalmente sui piani coordinati
In generale il k-volume di un parallelepipedo di dimensione minore eguale a k e' eguale alla radice quadrata della somma dei quadrati dei k-volumi dei k-parallelepipedi ottenuti proiettandolo ortogonalmente sui k-piani coordinati.
- Si consideri un parallelogramma nello spazio di vertici O, v, w, v+w lo si chiama generato da v e w, e analogamente si dice k-parallelepipedo generato da v_1 ... v_k in R^n quello di vertici
O, v_1 , ... , v_k, v_1+v_2, ..., v_1+ v_k, v_2+v_3 , ..., v_2+ v_k, ... ... , v_1 +...+ v_k.
Poiche' proiettare ortogonalmente un punto di R^n su un k-piano coordinato significa annullare le n-k coordinate a cui non contribuiscono i vettori del sistema di riferimento che sono nel k-piano scelto,
se M e' la matrice con n righe e con k colonne queste essendo v_1 ... v_k ,
quanto sopra scritto si traduce in formule:
Volume generato da v_1 ... v_k =
radq ( somma al variare di Q tra le sottomatrici di M quadrate con k righe e k colonne dei (det Q )^2 )
In particolare in R^3 se v=(p,q,r), w=(A,B,C)
Area generata da v , w =
= radq( area((q,r),(BC))^2 + area((p,r),(A,C))^2 + area((p,q),(A,B))^2 )=
= radq ( (qC-Br)^2 + (pC -Ar)^2 + (pB-Aq)^2 ) =
= | v| | w| |sin v O w | = | v x w |
In R^2 (k=1) si riottiene il teorema di Pitagora (1-volume= lunghezza).
-In particolare essendo v x w del tipo t (Cq - rB, rA-Cp,pB-qA), t>0, deve essere
| t (Cq - rB, rA-Cp,pB-qA)|= | v| | w| |sin v O w | = radq ( (qC-Br)^2 + (pC -Ar)^2 + (pB-Aq)^2 )
e quindi |t|=t=1:
per cui v x w =(Cq - rB, - (Cp-rA) ,pB-qA).
Le coordinate del prodotto vettoriale sono i volumi orientati dei parallelepipedi
(con basi le proiezioni sui piani coordinati del parallelogramma generato da v e w) generati da
((1,0,0) (0,q,r) (0, B,C)) ((0,1,0) (p,0,r) (A, 0, C)) ( (0,0,1) (p,q,0) (A,B,0))
Interpretazione geometrica dello sviluppo per colonne
u=(a,b,c,), v=(p,q,r), w=(A,B,C) in R^3
det (u|v|w)=
det ((a,b,c), (p,q,r), (ABC)) = a(qC-Br) - b(pC -Ar) + c(pB-Aq) = u. (v x w)
considerando la relazione del coseno con il prodotto scalare si ha quindi
det (u|v|w) = |u| |v| |w| cos( u O vxw) | sin v O w |
(il segno, cioe' l'orientazione, puo' essere solo dato dal fatto che rispetto al piano per l'origine di v e w il vettore u stia o meno dalla stessa parte di vxw)
Breve compendio sul determinante nel piano e nello spazio: DVI , PDF .
.5-11-09 esercitazione 14 (30 minuti)
Calcolo di aree di triangoli nello spazio, calcolo di determinanti.
Regola di calcolo dei determinanti di matrici tre righe e tre colonne detta di Sarrus
det(( a,b,c) (d,e,f) (g,h,i))=
differenza tra la somma dei prodotti delle diagonali che scendono
con la somma dei prodotti delle diagonali che salgono=
=aei + bfg + cdh − [ceg + afh + bdi]
9-11-09 lezione 16 ( 20 minuti)
Teorema 1 ter sul determinante e segno di una permutazione: cfr. appunti precedente lezione.
9-11-09 esercitazione 15 (1 ora e 40 minuti)
Semplificare [6^3/ (1/6)^2 - 5]/ [(2^5)^{-3} ((2^4)^2)^2], log_{radq 2} [2/( radcub 4)],
log_{radq 3} 2 +log_{radq 3}(2-1/2) +log_{radq 3}(2-1/3) +log_{radq 3}(2-1/5).
Trovare ove e' definita l'espressione seguente e disegnare la zone del piano cartesiano determinata
da tali coppie (x,y)
radq x log( |x|-|y|) + log (1-x^2-y^2)
Disegnare la regione del piano cartesiano degli (x,y) per cui: 2 |x| +|y| <1 e x^2+y^2 , 16
Disegnare la regione del piano cartesiano degli (x,y) per cui: |2x+y-1| + x+ |y| <3
(da ultimare a casa)
10-11-09 lezione 17 ( 20 minuti)Riferimenti:[MA1] cap. 2 pagg. 90-91, Esercizi 2.74, 2.76, 2.80, [VV]
cap. 11 pagg.270-271
Numero delle combinazioni con ripetizione di M oggetti su N
ovvero il numero di possibili risultati, ignorando l'ordine, di M estrazioni con reimmissione in un'urna contenente N oggetti distinguibili
ovvero il numero di modi per ripartire di M oggetti eguali in N posti distinti lasciandone eventualmete alcuni vuoti (raggruppare M oggetti in N posti ``numerati'' lasciandone eventualmente alcuni vuoti:
se un numero H tra 1 ed N viene estratto metto un oggetto al posto H-esimo)
ovvero il numero di modi per distribuire ad N diverse persone di M oggetti eguali eventualmente non distribuendo nulla ad alcuni (se una persona viene estratta le si da un oggetto)
etc ... (insieme dei risultati di lanci ripetuti di dadi, insieme dei risultati di giri ripetuti di roulette, possibili frequenze fenotipiche in un campionamento su una popolazione etc ...)
Per calcolare questo numero uno dei tanti modi (simili) e' il seguente:
si allineano N+M-1 caselle (O nell'esemplificazione grafica)
OOOOOO .... OOOO
e se ne scelgono N-1 distinte (al posto della O si mette una X)
per esempio XOOOXXO ...XOOX
Il numero di queste scelte e' il numero delle combinazioni semplici di N-1 su N+M-1 cioe' il fattore binomiale (N+M-1)! /[(N-1)! M!]
Si vede ora come interpretare la scelta fatta come combinazione con ripetizione di M su N:
si nota che le O rimaste sono esattamente M
mettendo le crocette si sono creati N gruppi (eventualmente vuoti) di O tra le M rimaste
(primo gruppo: le O prima della prima X, k-esimo gruppo: le O tra la (k-1)-esima X e la k-esima X ...
(N-1)-esimo ed ultimo gruppo le O dopo l'ultima X)
nell'esempio: primo gruppo vuoto, secondo gruppo 3 elementi, terzo gruppo vuoto, ... , penultimo gruppo
2 elementi, ultimo gruppo vuoto
Ripetendo con altre parole: messo in corrispondenza il k-esimo gruppo con il k-esimo posto
si sono distribuiti in N posti, ordinati, eventualmente vuoti, M oggetti
il numero delle O che precedono la prima X e' il numero degli oggetti messi al primo posto
il numero delle O tra (k-1)-esima e k-esima X(0<k<N-1) e' il numero degli oggetti messi al k-esimo posto
il numero delle O dopo la (N-1)-esima X e' il numero degli oggetti messi al (N-1)-esimo posto
Altrimenti: si sono fatte M estrazioni con reimmissione di N oggetti S(1), S(2), ..., S(N)
il numero delle O che precedono la prima X e' il numero delle estrazioni di S(1)
il numero delle O tra (k-1)-esima e k-esima X(0<k<N-1) e' il numero delle estrazioni di S(k)
il numero delle O dopo la (N-1)-esima X e' il numero delle estraioni di S(N-1)
nell'esempio S(1) non e' stato estratto, S(2) e' stato estratto 3 volte, S(3) non estratto, ...,
S(N-1) estratto 2 volte, S(N) non estratto.
CONCLUSIONE
numero delle combinazioni con ripetizione di M oggetti su N =
numero delle combinazioni semplici di N-1 oggetti su N+M-1 =
numero delle combinazioni semplici di M oggetti su N+M-1 =
fattore bionomiale N+M-1 su M = (N+M-1)! /[(N-1)! M!] =
numero delle combinazioni con ripetizione di N-1 oggetti su M+1 posti
10-11-09 esercitazione 16 (1 ora e 40 minuti)
segno di trinomi di secondo grado
condizioni ``fantasma''
sistemi di diseguaglianze
attenzione a: diseguaglianze con una radice pari ad uno dei membri,
elevare al quadrato i membri di una diseguaglianza quando il segno di qualche membro non e' determinato.
espressione delle soluzioni come unione di intervalli
in quante maniere si possono distribuire a 4 persone 37 monete da un euro dando almeno un euro a persona?
si mettono in fila le 37 monete e si scelgono 3 distinti spazi tra le monete: si sono creati 4 gruppi non vuoti,
quello delle monete prima del primo spazio scelto, quello tra primo secondo spazioscelto , quello tra secondo e terzo, quello delle monete dopo il terzo
O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O
per esempio OSO O O O O O O O O O OSO O O O O O O O O O O O O O O O OSO O O O O O O O
quelle del primo gruppo vanno alla prima persona e cosi via.
Quindi ogni distribuzione corrisponde a scegliere 4-1= 3 spazi distinti sui 37-1=36 disponibili
Le possibili distribuzioni sono 36!/[3! 33!] = 6 x 35x34.
in quante maniere si possono distribuire a 4 persone 37 monete da un euro?
PRIMA SOLUZIONE (usata a lezione per introdurre il concetto di combinazione con ripetizione):
come prima si mettono in fila le 37 monete e si scelgono 3 spazi
ma non solo tra quelli intermedi : si possono scegliere anche lo spazio che precede la prima e quello che segue l'ultima
e si puo' scegliere piu' volte lo stesso spazio (nela caso si metteno le scelte contigue).
Si sono creati 4 gruppi eventualmente vuoti,
quello delle monete prima del primo spazio scelto, quello tra primo secondo spazio scelto , quello tra secondo e terzo, quello delle monete dopo il terzo
O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O
per esempio SO O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O OSS
quelle del primo gruppo vanno alla prima persona e cosi via. Nell'esempio la prima persona non prende nulla, la seconda 37, la terza nulla,
la quarta nulla.
Quindi ogni distribuzione corrisponde a scegliere con ripetizione 4-1= 3 spazi sui 37+1=38 disponibili
Le possibili distribuzioni sono le combinazioni con ripetizione di 3 oggetti ``identici'' su 38 posti ``numerati'' : (38+3-1)! / [3! 37!] = 40!/ [3! 37!]= 20 x13x38.
SECONDA SOLUZIONE (una volta noto il concetto di combinazione con ripetizione):
piu' direttamente e' il numero di combinazioni con distribuzione di 37 oggetti su 4 posti quindi (37+4-1)!/[(4-1)! (37+4-1-(4-1))!] = 40!/[3!37!].
Esercizi lasciati:
su una scacchiera rettangolare fatta di quadratini unitari, di base M quadratini e altezza N quadratini, quanti sono i cammini (con lati unitari o verticali o orrizzontali) che congiungono il vertice in basso a sinistra con il vertice in alto a destra, e di lunghezza minima?
quanti sono i monomi con coefficiente 1 di grado m in n variabili?
12-11-09 lezione 18 ( 20 minuti)
Fattore multinomiale
numero di anagrammi di una parola con m caratteri da scegliere tra n simboli distinti
ognuno con numero di occorrenze prefissato m_1, ..., m_n (quindi m_1+...m_n=m):
m!/(m_1! ... m_n!)
Formula multinomiale (per prodotti commutativi)
(y_1 + ... +y_n)^m = sommatoria al variare di m_1 ... m_n tra i numeri non negativi per cui
m_1+ ...+ m_n =m di m!/(m_1! ... m_n!)
nel caso n= 2 si riottiene la formula del binomio di Newton
(y_1+y_2)^m = somma al variare dei numeri nonnegativi m_1+m_2 = m di m!/(m_1! m_2!)
[ma m_2= m- m_1, e sono non negativi, posto m_1=k sta tra 0 ed m]
= somma al variare di k di m!/[k!(m-k)!]
12-11-09 esercitazione 17 (1 ora e 40 minuti)Riferimenti: applicazione di sistemi di disequazioni
``lineari '' (diseguaglianze con prodotti cartesiani): un esempio elementare di problemi di ottimizzazione e programmazione lineare. [EB] cap.3 pagg. 78-82 esercizi 3.5.2, 3.6.3-3.7.7; [MA1] cap. 4.2 pagg. 165-166, problema guida 4.1 pag 213, esercizi 4.17-4.21 pagg. 218-219; [VV] cap. 4.2 pagg. 62-65 esercizi 4.2.1-4.2.4, cap.4.3 pagg. 68-69.
-Numero dei monomi di coefficiente 1 di grado m in n variabili
considerando l'operazione non commutativa=
numero delle parole di m caratteri che si scrivono con n lettere = [ formula multinomiale]
somma dei numeri di anagrammi di parole con m caratteri da sceglersi
tra n simboli senza specificare quante volte un simbolo compare =
numero funzioni da {1, ... , m} a {1,..., n} =
numero delle disposizioni con ripetizione =
=n^m
-Numero dei monomi di coefficiente 1 di grado m in n variabili
scelto un ordine delle variabili e scrivendo le variabili del monomio nell'ordine =
numero dei risultati senza contare l'ordine di m estrazioni con riemmissione
di n oggetti distinti = etc. etc. =
numero delle combinazioni con ripetizione =
= binomiale n+m-1 su n-1 = n+m-1 su m
-Soluzione dell'esercizio:
su una scacchiera rettangolare fatta di quadratini unitari, di base M quadratini e altezza N quadratini, quanti sono i cammini (con lati unitari o verticali o orrizzontali) che congiungono il vertice in basso a sinistra con il vertice in alto a destra, e di lunghezza minima?
un cammino deve avere almeno lunghezza M+N poiche' per andare da (0,0) a (M,N) devo muovermi almeno di M in orizzontale e di N in verticale
d'altronde il cammino che segue un paio di lati, per esempio (0,0), (0,1) ... (0,N), (1,N), (2, N) ... (M,N), e' lungo M+N
quindi la lunghezza minima e' M+N
quali sono i cammini di lunghezza minima? sono le ``scale che salgono in avanti'' sono i cammini che non hanno tratti ne ``in basso'' ne ``a sinistra''
si puo' specificare un cammino dando le istruzioni: primo passo ``a destra'', secondo passo ....
per un cammino di lunghezza minima saranno solo M+N istruzioni ognuna o ``a destra''D o ``in alto'' A:
quindi un'istruzione e una parola
lunga M+N
scritta
ove D compare M volte
e A compare N volte.
Percio' un anagramma di A ... A (M volte) D ... D (N volte), quindi i cammini cercati sono (M+N)!/(M! N!)
Si nota che la formula non cambia se si scambiano M ed N. Infatti se si guarda ``di traverso'' la scacchiera le A si scambiano con le D.
- Collegamento con le combinazioni con ripetizione:
quindi il numero dei risultati senza contare l'ordine di M estrazioni con reimmissione di N+1 oggetti
cioe' il numero dei risultati senza contare l'ordine di N estrazioni con reimmissione di M+1 oggetti
e' il numero di anagrammi di A ... A (M volte ) B ... B (N volte) [si pensi alla dimostrazione della scorsa lezione]
Per accorgersene direttamente senza usare la formula del coefficiente binomiale si puo' ragionare graficamente:
per ogni anagramma con A e D sulla scacchiera, partendo da (0,0), si traccia un trattino verticale se c'e' una A, oppure un trattino orizzontale se c'e' una D
si e' tracciato il cammino
ora si aggiunge una (M+1)-esima colonna verticale adiacente dopo (M,0)
e si aggiunge un trattino orizzontale, da (M,N+1) a (M+1, N+1), sopra questa colonna
infine per ogni colonna si evidenzia di quanto e' aumentata l'altezza dalla colonna successiva
e si contano le caselle evidenziate ottenendo dei numeri:
y_1, ..., y_M, y_{M+1} la cui somma evidentemente e' l'altezza raggiunta cioe' N
quindi per ogni cammino si trova una distribuzione di N oggetti ad M+1 persone, e viceversa.
-Richiamo su diseguaglianze lineari: semipiani. I sistemi di diseguaglianze individuano nel piano
poligoni o intervalli o punti cioe' le inetrsezioni dei singoli semipiani definiti da ciascuna diseguaglianza.
Intersezione di convessi e' convessa: quindi essendo i sempiani convessi le loro intersezioni saranno poligoni convessi
- Problema guida 4.1 pag. 213 ed esercizio 4.21 pag. 219 in [MA1]
nell'esercizio si tratta di aggiungere il vincolo sul costo
20 >o = 4a_1 + 2b_1
al problema guida:
trovare il massimo di 4a_1 +b_1 + 2a_2 + 2b_2
0 < o = a_1
10 > o = a_1
0 < o = b_1
20 > o = b_1 che identifica il rettanglo di base (0,0)-(10,0) e altezza (0,0)-(0,20)
0 < o = a_2
10 > o = a_2
0 < o = b_2
20 > o = b_2
10 = a_1 + a_2
20 = b_1 + b_2
per cui sostituendo si tratta di trovare
il massimo di 2a_1 -b_1 +60
per (a_1, b_1) nell'intersezione tra il rettangolo e il semipiano definito da 20 >o = 4a_1 + 2b_1
che e' il triangolo di vertici (0,0), (0,10), (5,0)
ora il massimo di 2a_1 - b_1 +60 si ha quando b_1 e' minimo cioe' 0 quindi per a_1 massimo
cioe' 5. ottendo 70.
un altro modo di procedere e' praticamente grafico e in casi piu' complessi molto piu' utile
tenendo presente
1- l'insieme dei punti del piano (x,y) per cui P x+ Qy =c e' una retta
e al variare di c sia hanno retta parallele che riempiono il piano
2- i valori massimo e minimo che Px+Qy assume quando (x, y) varia
in un insieme convesso (con i suoi bordi e vertici) sono c_1 e c_2 per cui
l'insieme convesso e' compreso nella striscia tra le due rette parallele
di equazioni Px+Qy - c_1=0 e Px+Qy - c_2=0 ( (x,y) : min{c_1, c_2} , o = Px+Qy ,o= max{ c_1, c_2})
ovvero le due rette ``estreme '' che toccano il convesso tra quelle parallele a Px+Qy=0
3-l'insieme dei punti del convesso in cui uno di questi valori e' assunto
o e' fatto da un solo vertice o da un lato del convesso (che sarebbe in comune con la retta estremale)
nel caso poiche' le rette 2a_1 -b_1 +60 -c =0 non sono parallele ai lati del triangolo il valore massimo deve essere in uno degli estremi per cui la retta intereca il triangolo solo nel vertice:
si sostituisce e si calcola e si vede quale dei due vertici da il valore massimo:
(0,10) c=50
(5,0) c=70
e saranno quelle rette che intersecano il triangolo con intersezione verticale di valore minimo
poiche' se voglio il massimo di c= 2a_1 -b_1 +60 , devo rendere massimo il termine noto di
2a_1 -b_1 +60 -c
Esercizio lasciato
Numero dei monomi di coefficiente 1 di grado m in n variabili scritti raggruppando in potenza le variabili eguali ma non potendo scambiare le potenze cosi ottenute di variabili diverse
(cioe' x^2y va considerato diverso da y x^2)
16-11-09 esercitazione 18 (ore 2) Diseguaglianze trigonometriche e rotazioni nel piano
introduzione al prodotto (cartesiano) righe per colonne di una matrice con un vettore
-diseguaglianze
(t- radq(t) +1)/(t-1) >o= 0
l'espressione comporta le assunzioni t >o= 0, t non=1
ci si riconduce a forma piu' usuale ponendo x= radq(t)
e si ottiene il sistema
(x^2- x+1)/(x^2-1) >o= 0
x non = 1
x > o = 0
-diseguaglianze trigonometriche
sin 3x > 1/2, sin (log x) > radq(3)/2,
cos x -sin x >o= 0
2cos x -sinx >o= 0 - metodo parametrico t = cos x , s = sin x
si ha il sistema t^2+ s^2 =1 e 2t -s >o= 0
da risolvere graficamente e quindi estendere la soluzione
sommando multipli di 2 pig
- altro meodo discutere i casi cos x =0 , e cos x non=0 nel secondo
si divide per cos x e si hanno i due ultriori casi
cos x > 0 e 1- tan x > o = 0
cos x < 0 e 1 - tan x < o = 0
2cos x - sinx > 1 - metodo parametrico come prima
- altro metodo parametrico : si pone k =tan (x/2)
ci si ricorda che cos x = (1-k^2)/(1+k^2), sin x= 2k/(1+k^2)
sostituendo si ottiene
2(1-k^2) -2k > 1+k^2
che si risolve in k e quindi le diseguaglianze ottento su k
si trasferiscono, usando l'arcotangente, su x
polinomi omogenei in seno e coseno
cos x sin x - cos^2 x > 1 piuttosto che uno dei metodi parametrici
conviene scrivere il termine noto 1= cos ^2 x +sin^2 x
quindi discutendo a parte il caso cosx =0 dividere
per cos^2 x ottendeno la disequazione in q= tan x
q - 1 > q^2 +1
q= tan x
cos x sin x - cos^2 x > cos^4 x qui per esempio conviene vedere i due addenti del primo
membro moltiplicati per 1= cos^2 x + sin ^2 x
e dividere per cos^4 x ottenendo
q + q^3
Queste semplificazioni sono dovute al fatto che ci si riduce a disequazioni del tipo
a_n (sin x)^n + a_{n-1} (sin x)^{n-1} cos x + ...+ a_0 (cos x)^n > o= 0
ovvero
t= cos x
s= sin x
somme su k a_k s^k t^{n-k} = a_n s^n + a_{n-1} s^{n-1} t + ... + a_0 t^n >o= 0
pertando dividendo per t^n = (cos x )^n , facendo attenzione al segno di t^n e quando
negativo cambiando il verso della diseguaglianza nella disequazione, si ottengono
due sistemi disequazioni in q= tan x e una disequazione diretta per il caso cos x=0
a_n q^n + .... + a_0 >o = 0
cos x >0
a_n q^n + ... + a_0 <o= 0
cos x <0
a_n (sin x)^n >o= 0
cos x=0
- Calcolare le coordinate del ruotato in senso antiorario di pig/3 attorno all'origine
del punto (3, 2)
chiamiamo la rotazione R
R(3,2) sra' un punto di coordinate (a,b)
ora (teorema fondamentale dell'algebra lineare) una rotazioe si distribuisce sulla somma
e si scambia con il prodotto per numeri
tendeno presente che (3,2) = 3 (1,0) + 2(0,1)
R(3,2) = 3R(1,0) +2 R(0,1)
quindi basta trovare le quattro coordinate del ruotato per l'angolo A voluto
dei due vettore del sistema di riferimento cartesiano
ma questa per definizione sono
R(1,0) =(cos A, sin A)
R(0,1) =(-sin A, cos A)
nel caso (1/2, radq(3)/2) rispettivamente (-radq(3)/2, 1/2)
per cui
(a,b) = R(3,2) = 3 (1/2, radq(3)/2) + 2 (-radq(3)/2, 1/2) = (3/2, 3radq(3)/2)+ (-radq(3), 1)=
= (3/2 - radq(3), 3radq(3)/2+1)
a= 3/2 -radq(3)
b= 3radq(3)/2 +1
In generale dato il punto (x,y) e l'angolo A (con segno: rotazione antioraria A>0, rotazione oraria A<0)
le coordinate (a,b) del ruotato attorno all'origine per l'angolo A di (x, y) sono
a = x cos A - y sin A
b = x sin A + y cos A
ovvero si considera la matrice che ha come colonne i trasformati dei vettori del sistema di riferimento canonico
la prima coordinata del trasformato sara' :
il prodotto scalare della prima riga di tale matrice per le coordinate del vettore da trasformare
la seconda coordinata del trasformato sara' :
il prodotto scalare della seconda riga di tale matrice per le coordinate del vettore da trasformare
Questo e' vero in generale per tutte le trasformazioni lineari:
si fa la matrice che ha come colonne le coordinate dei trasformati dei vettori della base canonica
quindi la k-esima coordinate del trasformato di un vettore e' data dal prodotto scalare della
k-esima riga di tale matrice con le coordinate del vettore.
17-11-09 esercitazione 19 (ore 2)
Trovare le coordinate del ruotato intorno all'asse (0,0,1) di pig/3 ``in senso antiorario guardando dall'alto (0,0,1)'' del punto di coordinate (1,2,3).
Trovare una base cartesiana di vettori mutamente ortogonali di lunghezza unitaria
il cui terzo asse sia nella direzione di (1,1,1), e che sia equiorientata con il sistema
di riferimanto canonico.
Esercizi sui numeri complessi: selezione dagli esercizi di pagg.7-8 dalla raccolta del corso di
Matematica e Statistica C 2008-2009.
Per trovare le radici ennesime di un numero complesso se questo e' scritto in forma polare
w=r e^{i A} conviene ricordare che le radici ennesime sono i vertici di un ennagono regolare
inscritto nella circonferenza di raggio r^{1/n}, quindi, a partire da z_1= r^{1/n} e^{i A/n},
le altre n-1 radici, r^{1/n} e^{i A/n +i k 2 pig/n}, 0< k <o= n-1, si trovano spostandosi di un arco di 2pig/n dalla precedente sino a ritornare a z_1:
w= -81 radq(3)/2 - i 81/2 =81 e^{i 4/3 pig }
z^8 =w ha soluzioni:
z_1 = radq(3) e^{ i pig/6 }
z_2 = radq(3) e^{ i pig/6 + i 2 pig/8}=radq(3) e^{ i pig/6 + i pig/4}
z_3 = radq(3) e^{ i pig/6 + i pig/2}
z_4 = radq(3) e^{ i pig/6 + i3 pig/4}
z_5 = radq(3) e^{ i pig/6 + i pig}
z_6 = radq(3) e^{ i pig/6 + i 5 pig/4}
z_7 = radq(3) e^{ i pig/6 + i 3 pig/2}
z_8 = radq(3) e^{ i pig/6 + i 7 pig/4}
Esercizi lasciati:
-trovare le coordinate del ruotato in senso antiorario attorno a (3,4) per un anagolo pig/6 del punto (1,2)
-trovare le coordinate del ruotato del punto (1,2,3) attorno all'asse per l'origine e (1,1,1) per un angolo di pig/6 ``in senso antiorario guardando la punta del vettore dall'origine a (1,1,1)''.
19-11-09 lezione 19 ( ore 2) Riferimenti: [EB] cap. 3 pagg. 59 -89 anche ripasso, cap. 12 pagg. 381-384 ;
[MA1] cap 3 pagg.107-120, 129-134;
[BDM] cap 4 pagg. 139-158, 164-170, 171-178,
[VV] cap. 6 pag. 89-100.
La nozione astratta di funzione estensionale (grafico astratto) e quelle ad essa legati.
Si tratta di funzione estensionale quando ad ogni elemento di un insieme di dati ammissibili o interessanti
si associa un solo valore, e non importa come si calcola dal dato il risultato.
Per questo si scrive x--->f(x) per dire che la funzione f trasforma il dato x
nel risultato f(x) ed mediante f partendo da x non si possono ottenere altri risultati.
Si scrive anche f(x)=y per indicare che quast'unico risultato e' eguale a y.
L'insieme dei dati ammissibili o interessanti si dice dominio della funzione
L'insieme dei valori di una funzione in un dominio si dice immagine. Si scrive
f:A --->B o x in A, x ---> f(x) in B
intendendo una funzione definita sugli elementi di A , che li trasfroma in elementi di B
In particolare l'immagine di A tramite f sara' un sottoinsieme di B.
Esempi: una tabella a due colonne in cui la prima di elementi diversi definisce
una funzione che
ad ogni elemento della prima colonna associa l'elemento della seconda
colonna sulla stessa riga
(si noti che la tabella in se non specifica ne regole di calcolo ne procedure di
misurazione per passare da un dato all'altro)
associare i posti a sedere ai nomi degli occupanti (si noti che fare il contrario non e' detto dia
una funzione ... in casi di omonimia)
associare ad un numero x i numeri y per cui y^2=x
non e' una funzione da numeri a numeri
infatti per prima cosa la regola non da risultato se x e' negativo,
comunque rimane l'ambiguita' se ad x associare rad.quad.|x| piuttosto che -rad. quad.|x|.
Piuttosto:
associare ad un numero non negativi x l'insieme dei numeri y per cui y^2=x
e' una funzione da numeri ad insiemi
infatti dato x >o=0 e' ben determinato, solo usando x, l'insieme { rad.quad. x , -rad. quad. x}
x ----->{ rad.quad. x , -rad. quad. x}
Anche:
associare ad un numero non negativo x l'unico numero non negativo y per cui y^2=x
e' una funzione da numeri a numeri
x -----> rad.quad. x
Spesso una funzione e' specificata da una regola di calcolo in un certo linguaggio, e la stessa funzione puo' essere calcolata in modo diverso. Quando si specifica una regola di calcolo puo' accadere che l'espressione o programma che si scrive, per calcolare la funzione, introduca delle restrizioni agli ``input '' ammissibili, ovvero si ha una restrizione del dominio inteso.
Considerando le seguenti espressioni
x in R, f(x)=1; x in R g(x)= (x^2+1)/(x^2+1); x in R h(x)=(1-x)/(1-x)
si osserva che f e g sono la stessa funzione (f=g) seppur calcolata in modo diverso,
mentre h e' una funzione diversa poiche' la formula data per specificare la funzione si porta dietro la condizione x non= 1, e quindi h ha un dominio diverso da f, quindi pur dando lo stesso risultato di f nella parte di dominio comune e' diversa proprio perche' ha dominio diverso.
Una misura m finitamente additiva su un insieme X e' quindi una funzione con dominio uno
pseudoanello M di sottoinsiemi di X per cui valgono:
1) m(A) e' un numero reale non negativo
2) m(vuoto)=0
3) m(AUB) =m(A) +m(B)- m(A intersezione B)
di conseguenza
4) se A e' contenuto in B si ha m(A) =o< m(B)
m: M --> [0,+oo[
In particolare una probabilita' (finitamente additiva) P su un insieme X puo' essere definita
come una funzione con dominio un'algebra A di sottoinsiemi di X, che e' una misura per cui
5) P(X)=1
P: A ---> [0;1]
Per avere un rigore maggiore e far rientrare in un unico schema astratto casi motlo diversi fra di loro si puo' ridurre (appunto alla concezione estensionale) il concetto di funzione identificandolo con quello relazione binaria di tipo univoco, detto appunto anche funzionale (deve risultare chiaro che in altri contesti questa modo di considerare le funzioni non e' appropriato: si pensi al fatto che due programmi molto diversi possono calcolare la stessa funzione estensionale):
Definizione: f sottoinsieme di DXB (sottoinsieme di coppie ordinate o relazione binaria tra elementi di D ed elementi di B) e' una funzione se
(a,b) in f e (a,c) in f ==> c=b (il risultato e' determinato in modo unico dal dato a);
se f e' una funzione invece di (a, b) in f si scrive b=f(a) o anche f: a--> b.
Definizione: dati ammissibili o interessanti per una funzione: dominio
data f di tipo funzione come sottoinsieme di DxB essa si porta dietro il suo dominio
dom f={ x: esiste b in B per cui (x, b) in f} =
={ x: esiste b in B per cui f(x)=b }
Se si scrive f: A-->B si indende che A e' il dominio di f.
Nei vari casi A viene specificato a secondo dell'interesse o determinato dalle espressioni che si usano, il che si traduce spesso in equazioni o diesequazioni.
Definizione: l'iniseme dei valori di una funzione: immagine di una funzione f su un dominio C
se C e' un sottoinsieme del dominio A di una funzoine f (f:A-->B)
il sottoinsieme di B dato dai valori di f sugli elementi di C si dice immagine di f su C.
im_C f ={y in B: esiste x in C y=f(x)}= { f(x): x in C},
ATTENZIONE: Molto spesso si usa la notazione f(C), che puo' essere tavolta fuorviante visto che porta a confondere l'insieme dei valori con un valore.
Definizione: un sottoinsieme di una funzione si dice sua restrizione:
si dice restrizione di f a C insieme, la funzione che ha come dominio
C intersecato il dominio di f, e come valori quelli dati da f.
f|_C ={(a,b): a in dom f e a in C e b=f(a)}
Definizione: funzione composta di due funzioni
f: A--> B , g: H---> K se im_A f e' contenuto in dom g
si definisce la funzione composta di g con f denotata da gof
gof ( a) = g( f(a) )
gof : A ---> K , a --->f(a) ---> g(f(a))
Per far apprezzare il livello di astrazione possiamo definire la funzione Comp
che ad una coppia ordinata di funzioni (per esempio funzioni da numeri a numeri) associa la funzione composta della prima con la seconda:
dom Comp ={(g,f): dom g contiene im f } Comp((g,f)) = gof
Definizione: iniettivita' di una funzione f in un sottodominio C:
una funzione f si dice iniettiva su C se
per ogni a e b in C se f(a)=f(b) allora a=b,
vuol dire: per ogni termine noto y si ha al piu' una soluzione in C dell'equazione f(x)=y ,
o meglio per ogni valore y della funzione vi e' un'unica soluzione dell'equazione f(x)=y.
e.g. se al terzo posto e quinto vi sono sedute due ragazze di nome Simona la funzione che a posti associa nomi non e' iniettiva. Ma se si togli il quinto posto per esempio, e non vi sono altre omonimie la funzione ristretta ai posti meno il quinto e' iniettiva.
La funzione che ad x associa x^2 non e' iniettiva: x e - x danno lo stesso valore.
La funzione definita dallo stasso calcolo restringendosi agl x non negativi e' iniettiva.
La funzione che ad x associa sin x non e' iniettiva: x e tutti inumeri x + 2k pig con k in Z hanno lo stesso seno.
Una qualsiasi delle sue restrizoni a [-pig/2 + 2h pig, pig/2 +2hpig] sono funzioni iniettive (h in Z).
Definizione: surgettivita' di una funzione f in un sottodominio C su un insieme B:
per ogni b in B esiste c in C f(c)=b
vuol dire: per ogni dato y in B vi e' almeno una soluzione x in C di f(x)=y
Definizione: una funzione che sia iniettiva su C e surgettiva da C su B si dice bigettiva
Ogni funzione iniettiva su C e' bigettiva sulla sua immagine.
Definizione: funzione identica
su ogni insieme A e' definita la funzione x ---> x (x=f(x))
essa si chiama funzione identica, o identita', su A e si denopta con id_A, Id_A, id,Id
Definizione: funzione inversa
quando f: A--->B si dice che g:B-->A e' l'inversa di f
se g(f(x))=x per ogni x in A
ovvero se gof = id_A
Nel caso essa e' determinata in modo unico e si indica con f^{-1} .
Se una funzione ha l'inversa definita su B si dira' invertibile da B.
Si osserva che se g=f^{-1} allora f=g^{-1}, cioe' fog = id_B, cioe' f(g(x))=x per ogni x in B.
ATTENZIONE: la notazione dell'inversa e' eguale a quella del reciproco con le potenze
quindi bisogna distinguere se f e' invertibile per esempio a valori reali non nulli
il reciproco del valore di f : (f(x))^{-1}
dal valore dell'inversa di f : f^{-1} (x)
Teorema Una funzione f:A--->B e' iniettiva se e solo se e' invertibile dalla sua immagine.
La comprensione del concetto di funzione inversa e' reso ancor piu' semplice se si considera la
nozione di funzione dato come relazione binaria univoca
se un certo insieme di coppie (a,b) sono una funzione sottoinsieme di D X B allora
l'insieme di coppie (b,a) sottoinsieme di Bx D
e' una funzione g se e solo se f e' iniettiva e g sara' la sua inversa.
Il dominio dell'inversa e' l'immagine della funzione
l'immagine dell'inversa e ' il dominio della funzione:
in altri termini l'inversa dell'inversa e' la funzione.
Per questo motivo se si denota con una lettera (usualmente x) il generico elemento del dominio di f
e si denota con un'altra lettera (usualmente y) il generico valore di f (y=f(x)),
si denotera' con y il generico elemento del dominio dell'inversa di f e con x il generico valore dell'inversa di f ( f^{-1} (y)=x).
In certi casi non e' conveniente questo cambio di nomi come vedremo.
x--> arsin x , x in [-1,1]
e' l'inversa della restizione a [-pig/2, pig/2] della funzione x--> sin x , -pig/2 < o= x <o= pig/2
x--> artan x , x in R
e' l'inversa della restizione a ]-pig/2, pig/2[ della funzione x--> tan x , -pig/2 < x < pig/2
x--> arcos x , x in [-1,1]
e' l'inversa della restizione a [ 0, pig ] della funzione x--> cos x , 0 < o= x <o= pig
x--> radq x , x >o= 0
e' l'inversa della restizione a [0 , +oo] della funzione x--> x^2 , 0 < o= x
x--> log x , x >0
e' l'inversa della funzione x--> e^x , x in R,
l'inversa dell'identita' su A e' la stessa funzione
ma attenzione x--->1/x , x non= 0
e' l'inversa di x--->1/x , x non= 0
(la funzione che da il reciproco ha come inversa il ``reciproco'' (la funzione che da il reciproco))
Definizione: preimmagine di un insieme mediante una funzione:
data una funzione f e un insieme E l'insieme dei punti su cui f assume valore in E si dice
preimmagine di E mediante f. L'usuale notazione e':
f^{-1} (E) = {x in dom f: f(x) in E}
ATTENZIONE: la notazione f^{-1} (E) usa lo stesso simbolo che si usa per l'inversa: ma per fare la preimmagine non c'e' assolutamente bisogno che la funzione sia invertibile.
Se poi la funzione e' invertibile la notazione per la preimmagine di un insieme mediante f
coincide con quella dell'immagine di quell'insieme mediante f^{-1} .
FUNZIONI DI PIU' VARIABILI: se si considera una funzione f il cui dominio e' sottoinsieme di un prodotto cartesiano finito A_1x A_2 ... x A_n
f: A_1x A_2 ... x A_n ---> M
quando x = (a_1, ... a_n) e' un elemento del dominio pe scrivere f(x) volendo mettere in risalto le componenti di x e' comodo piuttosto che scrivere f((a_1, ... a_n)), scrivere semplicemente f(a_1, ... a_n).
Analogamente quando il dominio e' un prodotto cartesiano di prodotti cartesiani molto spesso e' comodo considerare la funzion nel comlesso delle variabili raggruppate, o raggruppate in modo diverso
e.g il prodotto scalare in R^2 puo' essere visto come G: R^2 x R^2 --->R o come funzione di quattro variabili a valori numeri ovvero come F:R^4 --->R:
se u=(x,y) e v=(a,b) xa+yb=u.v= F(x,y, a,b)= G((x,y),(a,b))
FUNZIONI VETTORIALI: se si considera una funzione f i cui valori sono elementi di un prodotto cartesiano
finito M_1xM_2 ... xM_n
f:A ---> M_1xM_2 ... xM_n
si osserva che essa e' determinata una volta che si hanno n funzioni ognuna rispettivamente a valori nel fattore del prodotto cartesiano:
f(p) = (f_1(p), ..., f_n (p) )
le funzioni f_1 :A ---> M_1, ... , f_n : A ---> M_n si dicono funzioni componenti.
e.g. Ad ogni studente associo nell'ordine l'eta' e l'altezza: si ha una funzione dall'iniseme degli studenti
ad R^2
Fissato un sistema di coordinate cartesiano la legge oraria di un moto piano
e' una funzione da R in R^2, ad opgni istante ho le due coordinate che determinano la posizione
quindi due funzioni a valori reali
un moto circolare uniforme e' dato dalla funzione t--->(cos t, sin t)
le due funzioni a valori reali t--> cos t e t ---> sin t determinano (e sono determinate)
dalla legge oraria
Un sistema in n incognite reali e k equazioni con termine noto (b_1, ..., b_k) =b puo' essere visto
come un'equazione per una funzione F definita in un sottoinsieme di R^n a valori in R^k
F:A contenuto in R^n ---> R^k F(x)=b
Una rotazione attorno all'origine di un angolo A in R^2 e' la funzione vettoriale di piu' variabili
F:R^2 --->R^2 F(x,y)= (x cos A- y sin A, x sinA + y cos A)
In generale una trasformazione lineare da R^n ad R^k sara' una funzione in n variabili con k
componenti, ogni funzione componente essendo espressa da somme di ``multipli'' delle variabili.
23-11-09 lezione 20 ( ore 1) Riferimenti: [EB] cap. 4 pagg. 90-97 ed esercizi, cap. 5.4 pagg. 115-119,
cap. 6 pagg. 146-162 ed esercizi, cap. 12 pagg. 381-384; [BDM] cap. 5 pagg. 179- 198, anche ripasso 202-214, cap. 6 pagg. 215-255 anche ripasso.
- Ripetizione di alcuni concetti esposti la scorsa lezione: preimmagine, e funzione inversa;
per esempio l'insieme delle soluzioni S di un sistema con n incognite e k equazioni
S= { (x_1 ... x_n) per cui valgono le condizioni
E_1(x_1 ... x_n)= t_1
.
.
.
E_k (x_1 ... x_n) = t_k}
ove i termini noti sono (t_1 ... t_k),
puo' essere visto come preimmagine dell'insieme {(t_1 ... t_k)}
costituito dalla sola k-pla dei termini noti
per la funzione E di n variabili e k componenti definita da
E(x_1 ...x_n) = (E_1 (x_1 ... x_n), ..., E_k(x_1 ... x_n))
per esempio un semipiano e' la preimmagine di una semiretta mediante una funzione lineare da R^2 in R
-Si ricordi: il dominio dell'inversa e' l'immagine della funzione
l'immagine dell'inversa e ' il dominio della funzione
- Per funzioni f: M --> R, a valori reali:
la preimmagine dell'insieme {c} costituito da un solo numero c si dice insieme di livello c di f
f^{-1} ({c}) = { x in M: f(x)=c}
la preimmagine della semiretta ]-oo ; c] o della semiretta ]-oo; c[ si dice sottolivello ( a partire da c) di f
f^{-1} (]-oo; c[ ) = { x in N: f(x) < o = c}
f^{-1} (]-oo; c[ ) = { x in N: f(x) < c}
la preimmagine della semiretta [c; +oo[ o della semiretta ]c; +oo[ si dice sopralivello (a partire da c) di f
f^{-1} (]-oo; c[ ) = { x in N: f(x) >o= c}
f^{-1} (]-oo; c[ ) = { x in N: f(x) > c}
il grafico della funzione (che in astratto per questa trattazione coincide con la funzione) si ricorda essere
f = Graf f= {(x,y) in N x R: y=f(x) }
si definiscono quindi
sopragrafico di f su A = {(x,y) in M x R: x in A e y >o = f(x) }
sottografico di f su A = {(x,y) in M x R: x in A e y <o = f(x) }
- Modi diversi di vedere un grafico di una funzione a valori reali
(vedere esercitazione per una discussione piu' articolata ed esempio)
il grafico di una funzione g, reale di variabile reale, {(x,y): x=f(x)} sottoinsieme di R^2
si vede come immagine di una funzione a valori nel piano
x---> h(x)=: (x, g(x)) (percorsi , cammini),
e anche come luoghi di zeri di una funzione di due variabili
f(x,y)= y-g(x)
- Il disegno del grafico dell'inversa per funzioni di una variabile reale a variabile e'
il simmetrico rispetto alla bisettrice del disegno di quello della funzione:
se si ha il disegno di funzione f iniettiva come grafico rispetto alla retta orizzontale delle ascisse
(cioe' come si usa di solito la prima componente a di un punto (a,b) di R^2 e' quella che si disegna come coordinata orizzontale)
( x , f(x) ) x in dom f
il grafico della sua inversa rispetto all'asse verticale (cioe' contrariamente all'uso comune considerando
la prima componente del grafico astratto come coordinata verticale cioe' come seconda componente nel disegno) e' il disegno stesso della funzione, fatto secondo convenzione, da cui si e' partiti:
( f^{1} (y) , y ) y in dom f^{-1} = im f
(in altri termini si descrive il grafico di f come immagine della funzione
h(t)= (f^{-1} (t), t) h: im f ---> R^2
mentre prima lo si descriveva come immagine di
k(t) =(t, f(t) ) k: dom f ---> R^2
vedere esercitazione)
invece, ed e' quello che interessa, il grafico dell'inversa rispetto all'asse orizzontale
(cioe' come si usa considarando la prima componente del grafico astratto anche come prima componente, componente orizzontale, nel disegno
ovvero
riservando come uso la lettera x per designare le coordinate orizzontali
e la lettera y per designare quelle verticali nel piano cartesiano
piuttosto che usare x per la ``variabile indipendente'' e y per quella ``dipendente''
visto che ci sono in gioco due funzioni per cui il dominio dell'una e' l'immagine dell'altra)
( x , f^{-1} (x ) ) x in im f= dom f ^{-1} ovvero
( f(y) , y ) y in dom f = im f^{-1}
si ha semplicemente scambiando il valore della coordinata orizzontale con quello di quella verticale
quindi poiche' lo scambio di coordinata orizzontale con quella verticale
(a, b) ---> (b,a)
graficamente non rappresenta altro che la riflessione rispetto alla retta bisettrice
il disegno dell'inversa rispetto all'asse orizzontale e' il simmetrico rispetto alla bisettrice
del disegno di partenza.
In particolare per individuare sull'asse orizzontale il dominio dell'inversa basta riportare tramite la bisettrice l'immagine della funzione dall'asse verticale a quello orizzontale.
- I grafici ``pittorici '' delle principali funzioni di una variabile reale a valori reali
f(x) =3, f(x) = ax +b, f(x) = x^2, f(x)= x^3, f(x) = x^{2n}, f(x)= x^{2n+1}
f(x)= sin x, f(x) = cos x = sin (x + pig /2), f(x) = tan x, f(x) =e^x, f(x) =1/x
da cui si deducono passando alle restrizioni e alle loro inverse i grafici di
f(x) = arsin x (dominio [-1, 1] immagine [-pig/2 , pig /2] per definizione)
f(x) = arcos x (dominio [-1, 1] immagine [0 , pig] per definizione)
f(x) = artan x (dominio R immagine ] - pig/2 , pig /2[ per definizione)
f(x) = log x (dominio ]0, +oo[ immagine R)
- Principali rette tangenti ai grafici descritti
y=1 e' tangente a y=sin x nel suo punto (pig/2, 1) e il grafico sta sotto tale tangente orizzontale
y=x e' tangente a y=sin x nel suo punto (0,0) e per x tra 0 e pig/2 il grafico sta sotto la tangente
y=x e' tangente a y=tan x nel suo punto (0,0) e per x tra 0 e pig/2 il grafico sta sopra la tangente
y= x+1 e' tangente a y =e^x nel suo punto (0,1) e il grafico sta sempre sopra la tangente
y= -x +2 e' tangente a y=1/x nel suo punto (1,1) e per x> 0 il grafico sta sopra la tangente
considerando che la simmetrica di una retta rispetto alla bisettrice principale
e' una retta con coefficiente anglare reciproco di quello della prima
x = 1 e' la retta verticale tangente a y= arsin x nel suo punto (1, pig/2 )
y=x e' tangente in (0,0) sia ad y=arsin x che a y=artan x
y=x-1 e' tangente a y=log x in (1,0) e il grafico sta sempre sotto la tangente
23-11-09 esercitazione 20 (ore 1)
-Risoluzione grafica di disequazioni per funzioni da R in R.
dato il disegno di un grafico {(x, f(x)): x in C}
dato b termine noto per risolvere graficamente la disequazione f(x) < b
si tracci la retta orizzontale di quota b
le soluzioni saranno le prime coordinate dei punti del grafico che sono sotto la retta.
-Determinare se una curva disegnata nel piano cartesiano e' una funzione,
determinare se e' una funzione iniettiva, disegnare il grafico dell'inversa.
- un sottoinsieme del piano e' un grafico di funzione (rispetto all'asse orizzontale) se le rette ]
verticali lo intersecano al piu' una volta
- il dominio di una funzione (vista come insieme di coppie) e' la sua prima proiezione
l'immagine e' la sua seconda proiezione.
- il grafico dell'inversa di una funzione reale di variabile reale si ottiene
facendo il simmetrico rispetto alla bisettrice {(x,x) : x in R} del grafico di partenza
- il dominio dell'inversa e' l'immagine della funzione (se la funzione e' invertibile)
l'immagine dell'inversa e' il dominio della funzione( se la funzione e' invertibile)
per individuare graficamente sull'asse orizzontale il dominio dell'inversa basta riportare tramite la bisettrice l'immagine della funzione dall'asse verticale a quello orizzontale.
- Si disegna una curva che e' un grafico, interseca l'asse orizzontale sette volte, per
valori positivi grandi della prima coordinata la seconda coordinata dei punti su tale grafico e' positiva grande, per valori negativi grandi in modulo della prima coordinata la seconda coordinata dei punti sul grafico e' anch'essa negativa.
Se si assume che sia il grafico di un polinomio cosa si puo' dire ?
per il teorema fondamentale dell'algebra sara' un polinomio di grado maggiore o eguale a 7
il grado sara' dispari poiche' la potenza piu' alta che compare cambia segno al cambiare segno della variabile inidpendente
il coefficiente dell'addendo di grado massimo sara' positivo poiche' il cambiamento di segno e' concorde
-Grafici di funzioni pari, di funzioni dispari, di funzioni periodiche.
- Se N e' un sottoinsieme di R considerata una funzione g:N-->R, y=g(x), (intesa come grafico)
le due funzioni
f : N x R --> R , z= f(x,y)= y - g(x)
h : N ---> N x R, (x,y)=h(t) =( t , g(t) ) i.e. x=t, y =g(t)= g(x)
permettono di vedere in altro modo il grafico di g:
g= Graf g = { (x,y) in Nx R: y=g(x) }
= { (x,y) in Nx R: y-g(x) =0 }
= livello 0 di f
= { (x, y) in Nx R: per qualche t in N si ha x =t e y=g(t)}
= { (t, g(t) ) } al variare di t in N
= immagine di N mediante h
A parole: f permette di vedere il grafico come luogo di zeri, h come cammino.
Si osserva che qualsiasi funzione h di variabile t a valori in NxR:
(x,y)= h(t) =(h_1(t), h_2(t) ) x= h_1(t) y = h_2(t) ,
per cui h_2(t) = g(h _1(t)) cioe' h_2 = goh _1
ha immagine che descrive un sottoinsieme del grafico di g
mentre una siffata funzione che oltre alla condizione
h_2 = goh _1
verifica anche
immagine di h_1 = dominio di g
ha immagine che descrive un tutta g.
Quindi la scelta sopra fatta x= h_1(t) = t e h_2 =g e' in un certo senso la piu' semplice per descrivere tutto il grafico di g come immagine di un cammino.
Infatti una curva (in questo caso il grafico di g) puo' essere percorsa in modi diversi
cioe' con diversi cammini.
- Data f(x,y)= (x,y) . (2,3) + 5 = 2x + 3y + 5, f: R^2 --> R
descrivere il grafico
determinare se il suo livello 0 e' un grafico
trovare una funzione di cui e' grafico
trovare una funzione che lo ha come immagine.
il grafico di f e' il piano nello spazio R^3 di equazione 2x+3y -z = -5
per trovare una funzione il cui grafico e' il luogo di zeri di f
f^{-1} ({0}) =
= livello 0 di f = { (x,y) : 2x+3y+5=0 } = retta in R^2 di pendenza -2/3 passante per (0, - 5/3) =
= grafico di g(x) = -2/3 x - 5/3
per vederlo come immagine basta considerare il cammino t---> (t, -2/3 t - 5/3 )
- Un modo ``forsennato'' di percorrere una retta:
l'immagine della funzione o se si preferisce del cammino
h(t) = ( t sin t , -2/3 t sin t -5/3) = t sin t (1, -2/3) + (0, 5/3)
e' sempre la retta 2x +2y +5 =0
solo che il cammino in questione la percorre per t >0 a partire da (0, -5/3 ) per t=0
oscillando attorno a tale punto con oscillazioni sempre piu' ampie
Esercizi lasciati:
-mostrare usando le definizioni di immagine e preimmagine che
f^{-1} (C U D) = f^{-1} (C) U f^{-1} ( D)
f^{-1} (C intersecato D) = f^{-1} (C) intersecato f^{-1} ( D)
f (A U B) = f (A) U f ( B)
-invece in generale mostrare che si ha solo
f (A intersecato B) e' contenuto f(A) intersecato f( B)
e trovare un semplice esempio per cui l'immagine dell'intersezione e' piu' piccola dell'intersezione delle immagini
-mostrare che vale l'eguaglianza se e solo se f e' iniettiva.
24-11-09 lezione 21 ( ore 1)
Breve riassunto dei principali concetti esposti nella precedente lezione: grafici come immagini e livelli, grafico inversa.
- Grafici ``pittorici '' di altre funzioni di base:
per a >1 non in Z f(x)= x^a, x> o = 0
per 0< a <1 non in Z f(x)= x^a, x> o = 0
per a< 0 non in Z f(x)= x^a, x > 0
In particolare i grafici di radq x, x>0, x^{1/2n}, x>0, x^{1/(2n+1)} x in R,
utilizzando la regola per i grafici delle funzioni inverse e, per n in N, osservando che
f_n(x) =x^{2n} sono funzioni iniettive sulla semiretta non negativa,
mentre g_n (x)= x^{2n+1} sono funzioni iniettive in R.
Per a >1 f(x)= x^a, in (0,0) ha tangente orizzontale
per 0< a <1 f(x)= x^a, x> o = 0 in (0,0) ha tangente verticale
- Definizione: funzione monotone:
f:A--> R si dice (monotona) crescente su A
p.o. x ,z in A se z >o= x allora f(z) >o= f(x)
f:A--> R si dice (monotona) decrescente su A
p.o. x ,z in A se z >o= x allora f(z) <o= f(x)
f:A--> R si dice (monotona) strettamente crescente su A
p.o. x ,z in A se z > x allora f(z) > f(x)
f:A--> R si dice (monotona) strettamente decrescente su A
p.o. x ,z in A se z > x allora f(z) < f(x)
OSSERVAZIONE: l'unione di grafici di funzioni crescenti non e' detto sia il grafico di una funzione crescente.
OSSERVAZIONE: se si conosce un punto del grafico di una funzione crescente allora il restante grafico deve essere nel primo e nel terzo quadrante di centro il punto dato .
Si ricorda che la corda con estremi sul grafico di una funzione f reale di variabile reale
definita su un intervallo
e' l'immagine per t in [0;1] di t(z,f(z)) + (1-t) (b, f(b)) =(b,f(b)) + t ((z, f(z)) -(b,f(b)))
cioe' l'insieme { (t z+ (1-t)z , t f(z) +(1-t) f(b)): t in [0;1] }
cioe' il pezzo di retta y= (x-b) (f(z)-f(b))/(z-b) + f(b)=x (f(z)-f(b))/(z-b) +f(b)-b (f(z)-f(b))/(z-b).
Definizione: il coefficiente angolare di una corda con estremi (b, f(b)) e (z,f(z)) sul grafico di f
(funzione definita su un intervallo I) si dice rapporto incrementale con centro b:
Rbf (z) = (f(z)-f(b))/ (z-b)
Teorema: una funzione e' monotona crescente [descrescente] su I intervallo se e solo se
ogni corda con estremi sul grafico ha pendenza non negativa [non positiva ]
cioe' per ogni b in I e per ogni z in I\{b}
Rbf (z) >o= 0 [<o= 0]
- RESTRIZIONE DI UNA FUNZIONE DI PIU' VARIABILI AD UN INTERVALLO CONTENUTO NEL DOMINIO:
z=f(x) , x=(x_1, x_2 ...) x in D
dato p = (p_1 , p_2 ... ) in D e una direzione v=(v_1, v_2 ...)
in modo che la retta per p paralella a v intersechi D in un intervallo
cioe' vi sia un in intervallo I per cui p.o. t in I p +t v in D
la funzione di una variabile g(t) = f( p +t v ) rappresenta la restrizione di f all'intervallo considerato.
- Si ricorda che un sottoinsieme C di uno spazio vettoriale si dice convesso se
per ogni coppia di suoi punti P e Q tutto il segmento con estremi questi due punti e' contenuto in C
cioe': p.o. P e Q in C e p.o. t in [0;1] si ha Q+t(P-Q) in C
Definizione: una funzione f definita su un insieme convesso C a valori reali si dice convessa su C se
il suo sopragrafico su C, {(x,y): f(x) <o= y e x in C }, e' convesso.
Teorema: una funzione f e' convessa su un convesso C se e solo se
il suo grafico sta sotto le corde con estremi su di esso
cioe' p.o. z, b in C per ogni x tra z e b f(x) <o= (x-b) Rbf(z) + f(b)
equivalentemente
p.o. t in [0;1] z, b in C f( tz +(1-t)b)) <o= tf(z) + (1-t) f(b)
OSSERVAZIONE: ora tz +(1-t)b e' il generico punto dell'intervallo, nel dominio di f, di estremi b e z
mentre tf(z) + (1-t) f(b) e' il punto ad esso proporzionale che sta nell'intervallo, nell'immagine di f,
di estermi f(b) e f(z).
Questo vuol dire che il grafico della funzione tra i punti (b,f(b)) e (z,f(z))
sta sotto la corda con gli stessi estremi (ovvero tale corda sta nel sopragrafico)
(tale corda e' il grafico della funzione lineare affine g:x--> (x-b) Rbf(z) + f(b), x tra b e z,
questa funzione e' quella che trasforma il generico punto nell'intervallo di estremi b e z in quello che ha la sua stessa proporzionalita' con gli estremi f(b) ed f(z) nell'intervallo dell'immagine
g(tz +(1-t)b) = tg(z) + (1-t) g(b)= tf(z) + (1-t) f(b)).
DIMOSTARZIONE:quindi se la funzione e' convessa visto che il sopragrafico contiene il grafico questa condizione e' soddisfatta. Viceversa se tale condizione e' soddisfatta a maggior ragione la funzione e' convessa
(il segmento con esrtemi punti del sopragrafico sta sopra il segmento che ha come estremi le proiezioni in verticale di quei punti sul grafico).
TEOREMA: una funzione e' convessa se e solo se
il suo grafico sta sopra i complementari delle corde con estremi su di esso
cioe' p.o. z, b in C per ogni x non tra z e b f(x) -f(b) >o= (x-b) Rbf(z)
DIMOSTRAZIONE: poiche' (z,f(z)) deve stare sotto la corda di estremi (b,f(b)) e (x, f(x)) il punto (x,f(x)) deve stare sopra la retta passante per (b,f(b)) e (z, f(z)). Con ragionamento analogo sincerarsi del viceversa.
OSSERVAZIONE: quindi se si conoscono solo due punti del grafico di una funzione convessa si puo' dire
che essa sta sotto la corda tra i due punti e sopra il complementare della stessa.
TEOREMA: una funzione f e' convessa su un intervallo C se e solo se
le corde con estremi sul grafico e un estremo fissato hanno pendenza crescente al variare
dell'altro estremo in un piano verticale
cioe' per ogni b in C e per ogni direzione v la funzione t--->Rbf(b+tv), t numero non 0, e'
crescente.
DIMOSTRAZIONE: un argomento geometrico e' semplice, due casi :
. se il centro b del rapporto incrementale non e' in mezzo agli altri due punti
x, z essendo quest'ultimo il piu' lontano da b, si ottiene che (x,f(x)) deve stare sotto la corda
di estremi (b, f(b)) e (z,f(z)): quindi Rbf(x) < o= Rbf(z)
.. se piuttosto il centro e' ``al centro'' e poniamo che z venga prima di b ed x, il punto (z, f(z)) deve stare sopra la retta passante per (x,f(x)) e (b,f(b)) ma ... allora la velocita' uniforme per recarsi da f(z) a f(b) debbe esser maggiorata da quella invariata per condursi da f(x) allo stesso f(b).
Viceversa immediatamente da tale proprieta' di monotonia si deduce quella della corda, piu' sopra provata esser equivalente alla convessita'.
- PROBLEMATICA GENERALE DELLE FUNZIONI A VALORI REALI
1) come riconoscere in una legge data da formule l'andamento grafico della funzione
(ove aumenta ove diminuisce, il tipo di inflessione, l' area di parti di sopragrafico e sottografico etc. )
2)viceversa dato un andamento grafico come scrivere una legge con esso compatibile.
I teoremi che riducono la monotonia della funzione allo studio dei segni dei rapporti incrementali
e la convessita' allo studio della monoonia dei rapporti incrementali enunciati in questa lezione
sono il primo passo per affrontare tali domande.
L'ulteriore semplificazione e':
invece di studiare le pendenze delle corde sul grafico (rapporti incrementali)
studiare quelle delle rette tangenti (quando esistano: le derivate)
tali pendenze di tangenti, a livello intuitivo, sono i limiti dei rapporti incrementali per un'estremo della corda che si avvicina al secondo.
Questa e' tra l'altro una delle motivazioni per dare una rapida panoramica sui limiti in generale.
24-11-09 esercitazione 21 (ore 1)
-Pendenza di una retta simmetrica rispetto alla bisettrice ad una data.
-Grafici delle inverse di restrizioni a domini fatti da piu' intervalli distanti, di funzioni non iniettive.
-Grafici di f(x)=radq{|x|}, f(x)= x^{1/3}, f(x)= |x|^{1/3}, f(x)= segno di x, f(x)=parte intera di x,
f(x) =radq(1-x^2)
-Grafici di funzioni di due variabili in R^3 : f(x,y)= 2x+3y +5, f(x,y)=radq( x^2 +y^2), f(x,y)=radq(1-x^2-y^2)
-Se una funzione e' convessa su un intervallo senza estremi quali valori agli estermi si possono assegnare affinche' la nuova funzione sia convessa sull'intervallo compresi gli estremi?
26-11-09 lezione 22 ( ore 1e 30 minuti)
RIPETIZIONE
- RESTRIZIONE DI UNA FUNZIONE DI PIU' VARIABILI AD UN INTERVALLO CONTENUTO NEL DOMINIO:
z=f(x) , x=(x_1, x_2 ..., x_n) x in D sottoinsieme di R^n
dato p = (p_1 , p_2 ... ) in D e una direzione v=(v_1, v_2 ...) , || v || = 1
in modo che la retta per p paralella a v intersechi D in un intervallo
cioe' vi sia un in intervallo I per cui p.o. t in I p +t v in D
per t in I, per cui p+tv sta in D, in modo che f risulti definita, la funzione di una variabile g(t)= f( p +t v )
rappresenta la restrizione di f all'intervallo considerato, si vede in che senso:
i) si fa coincidere R^n con l'iperpiano ``orizzonatale '' di R^{n+1} con ultima coordinata nulla
{(x_1, x_2, ..., x_n , 0): (x_1 ...x_n) in R^n}
ii) si interseca
il grafico di f cioe' {(x_1, x_2 ..., f(x_1,x_2 ...)) : (x_1,x_2 ... ) in D} sottoinsieme di R^{n+1}
con il
piano ``verticale'' in R^{n+1} passante per la retta r={p +tv: t in R}, cioe'
{ (x_1, x_2 ... ,x_n, z) : x in r z qualsiasi}
e si ottiene
{ ( p+tv, f(p+tv)): t per cui p+tv in D} = {(p+tv, g(t)) : t in I}
alla lettera il grafico di f ristretta alla retta r={p +tv: t in R}
iii) si considera il grafico di g in R^2 cioe' {(t, g(t)) : t in I}
iv) si fa coincidere questo R^2 con il piano verticale in R^{n+1}di cui sopra in modo che:
l'asse delle ascisse vada a coincidere con la retta r
l'origine di R^2 di coordinate (0,0) vada a coincidere con il punto p=(p_1, p_2, ... p_n , 0 )
di conseguenza l'asse delle ordinate di R^2 viene a coincidere
con la retta in R^{n+1}``verticale sopra p'' cioe' {(p_1, p_2 ... p_n , z): z qualsiasi}
v) poiche' ||v||=1 le distanze dall'origine sulla retta orizzontale di R^2 sono eguali alle distanze da p sulla retta r
vi) il grafico di f ristretto ad r ottenuto al punto ii) coincide con il grafico tracciato in R^2 al punto iii).
- Grafici ``pittorici '' di altre funzioni di base:
per n>1 in N f(x) = x^{-n} = 1/(x^n) , x non 0
se n e' dispari f(-x)= -f(x), mentre se n e' pari f(x)=f(-x) quindi basta disegnare il grafico per x>0 e per completarlo
se n e' dispari lo si riflette per l'origine mentre
se n e' pari lo si riflette per l'asse verticale
se 0< x <1 f(x) < 1/x poiche' n >1
se x > 1 f(x) > 1/x
quindi per x >0 questi grafici
per x grande si avvicinano alla retta orizzontale stando sopra il grafico di 1/x,
per x vicino a 0 si avvicinano alla retta verticale stando sotto il grafico di 1/x
per n>1 in N f(x) = x^{- 1/n} = 1/(rad-n(x)) , x non 0 se n dispari, x> 0 se n pari
queste funzioni sono le inverse delle precedenti ( il reciproco elevato alla n della radice ennesima del reciproco di x e' x) quindi facendo la simmetria rispetto alla bisettrice principale
per x >0 tali grafici
per x grande si avvicinano alla retta orizzontale stando sotto il grafico di 1/x,
per x vicino a 0 si avvicinano alla retta verticale stando sopra il grafico di 1/x
Comportamenti del tutto analoghi hanno i grafici delle potenze negative:
per a< - 1 - a non in N f(x)= x^a, x > 0
per x >0 questi grafici
per x grande si avvicinano alla retta orizzontale stando sopra il grafico di 1/x,
per x vicino a 0 si avvicinano alla retta verticale stando sotto il grafico di 1/x
per -1<a< 0 -1/a non in N f(x)= x^a, x > 0
quindi, essendo le inverse delle precedenti, per x >0 questi grafici
per x grande si avvicinano alla retta orizzontale stando sotto il grafico di 1/x,
per x vicino a 0 si avvicinano alla retta verticale stando sopra il grafico di 1/x
-COME SI TRASFORMANO I GRAFICI AGENDO IN MODO LINEARE SEPARATAMENTE SU OGNI VARIABILE
x--> ax +b
y--> cy +d
Si tratta dato il disegno del grafico di f disegnare il grafico della funzione
g(x)=c f(ax+b) +d
Si fa passo per passo:
g(x) = f(x +c)
si trasla orizzontalmente il grafico di f portando l'origine in ( - c, 0 )
(a sinistra se c >0 , a destra se c<0:
se f avesse uno zero in 0 g avrebbe uno zero in -c)
g(x) = f(x) + c
si trasla verticalemte il grafico di f portando l'origine in ( 0, c)
g(x) = f(cx), c >0
se c>1 si `` comprime verso la retta verticale di un fattore 1/c'' il grafico
se 0< c<1 si ``dilata dalla retta verticale di un fattore 1/c'' il grafico
(se il primo zero non negativo di f fosse a il primo zero non nagtivo di g sarebbe a/c)
g(x) = c f(x), c>0
se c>1 si `` dilata dalla retta orizzontale di un fattore c'' il grafico
se 0< c<1 si ``comprime verso la retta orizzontale di un fattore c'' il grafico
g(x) = -f(x)
si riflette il grafico rispetto all'asse orizzontale
g(x) = f(-x )
si riflette il grafico rispetto all'asse verticale
In particolare
i grafici di funzioni pari non cambiano passando da x a -x
i grafici di funzioni dispari non cambiano passando da x a - x e da y a -y
i grafici di funzioni periodiche di periodo T non cambiano traslando orizzontalemye per T o per -T.
26-11-09 esercitazione 22 (30 minuti)
-Dato il grafico y=f(x) disegnare il grafico di |f(x)|, f(|x|)
- partendo da y= 1/x ---> a/x --> a/(x+b) ---> c + a/(x+b) si ottiene il grafico dell'ultima funzione:
che risultera' un'iperbole equilatera dilatata di un fattore a non 0 , eventualmente riflessa se a<0,
traslata in orizzontale per - b e in verticale di c
- grafici di y= (ax +b)/(cx +d) con i numeri c ed a non 0. Ci si riduce al caso precedente algebricamente:
(ax +b)/(cx +d) = a/c (cax +cb)/(acx +ad) = a/c (cax +ad + cb -ad)/(acx +ad) =
= a/c [ (cax+ad)/ (acx+ad) +(cb-ad)/ (acx +ad)] =
= a/c [ 1 +(cb-ad)/ (acx +ad)] =
= a/c [ 1 +(b/a-d/c)/ (x +d/c)]=
= a/c + (b/c-ad/c^2)/ (x +d/c)]
- Quante sono le funzioni da {1, 2 ..., k} a {1,2, ..., n}?
- Quante sono le funzioni iniettive da {1, 2 ..., k} a {1,2, ..., n}?
30-11-09 lezione 23 (30 minuti)
Distribuzione ipergeometrica:
Se si fanno n estrazioni, da una popolazione di N oggetti, senza riemmissione, e interessa la probabilita' di un evento (a prescindere dall'ordine in cui avvengono le estrazioni) il modo di ragionare, che conduce alla distribuzione binomiale, usato per calcolare la probabilita' che i ``successi'' siano esattamente m
non risulta comodo in quanto le successive estrazioni non sono piu' indipendenti e dopo ogni estrazione cambia la distribuzione di probabilita'.
Conviene ragionare pensando che l'evento elementare sia la singola scelta di n oggetti sugli N a disposizione, piuttosto che la singola estrazione di un oggettto prima sugli N disponibili , quindi suigli N-1 rimanenti e cosi via.
Quindi il numero di casi possibili e' il fattore binomiale N su n.
Se p(m) e' la probabilita' di ottenere esattamente m ``successi'' in n estrazioni senza reimmissione si puo' pensare che gli N oggetti a disposizione siano divisi in due:
M oggetti che danno il ``successo'' e i rimanenti N-M danno ``l'insuccesso''.
I casi favorevoli sono quelli in cui k delle estrazioni sono tra i primi M oggetti e le rimanenti n-m estrazioni sono tra i rimanenti N-M oggetti.
Quindi il numero dei casi favorevoli e' eguale:
il numero di sottoinsiemi con m elementi in un insieme con M elementi
moltiplicato
il numero di sottoinsiemi con n-m elementi in un insieme con N-M elementi
cioe'
binomiale M su m x binomiale (N-M) su (n-m).
Per cui pensando alla probabilita' come ``numero di casi favorevoli su numero di casi possibili'' la relazione che deve sussistere
p(m) = probabilita' che su n estrazioni senza reimmissione
su una popolazione di N oggetti suddivisa in due sottopopolazioni la prima con M elementi
si trovino esattamente m elementi della prima sottopopolazione=
= (M su m ) (N-M su n-m) / (N su n)
Piu' formalmente
Definizione: Sia P: A ---> [0;1] una probabilita' su un'algebra di sottoinsiemi di un insieme E
si dice che Y: E --> R ha distribuzione ipergeometrica di parametri (N,M, n) se
P(Y =m) = (M su m ) x (N-M su n-m) / (N su n)
Chiaramente cosi come la legge binomiale si generalizza con la legge multinomiale
quando non interessa solo il numero di successi ma piu' di due diversi possibili risultati
(e.g. lancio di un dado piuttosto che lancio di una moneta)
cosi la legge ipergeometrica si generalizza quando si fanno n estrazioni senza reimmissione su N oggetti
suddivisi in k sottopopolazioni ognuna rispettivamente con
M_1 , M_2 , ... , M_{k-1}, M_k = N - M_1 - ... - M_{k-1} elementi:
probabilita' che su n estrazioni senza reimmissione su n oggetti m_1 stiano nella prima sottopopolazione
... m_k nell'ultima sottopopolazione =
= (M_1 su m_1 ) x ... x (M_{k-1} su m_{k-1}) x (N- M_1 - ... - M_{k-1} su n-m_1 - ... m_{k-1}) / (N su n)
Funzioni positivamente omogenee:
Come visto nelle lezioni ed esercitazioni precedenti per avere un'idea approssimativa del grafico pittorico di una funzione di due variabili e a valori reali z=f(x,y), puo' essere conveniente studiare i grafici delle sue restrizione a intervalli z=g(t) = f(a + tu, b+tv) (u^2+v^2=1) e studiare, quando risulti agevole, anche gli insiemi di livello {(x,y): f(x,y)=c} al variare di c.
Negli esercizi svolti si avevavo funzioni i cui valori dipendevano solo dalla distanza dall'origine (0,0) del punto (x,y): gli insiemi di livello erano cioe' circonferenze e le restrizioni alle semirette spiccate dall'origine erano grafici noti. Per cui il grafico di f non era che il ruotato attorno all'asse delle z di
uno di questi grafici (per esempio quello di z=f(x,0)).
Si trattave di funzioni a simmetria radiale di centro l'origine (0,0): f(x,y) = g( x^2 +y^2).
cioe'
sono le funzioni che in coordinate polari (r, s) x = r cos s, y = r sin s,
non dipendono dall'angolo s: f(x,y) = h(r).
Un altro caso particolare interessante e' quello delle cosi dette funzioni positivamente omogenee di grado d e centro (0,0)
Definizione: f: D ---> R si dice omogenea di grado d ( d in Z) e centro (0,0) se
f(tx, ty) = t^d f(x,y) per t non 0 e (x,y) non = (0,0)
f: D ---> R si dice positivamente omogenea di grado d (d in R) e centro (0,0) se
f(tx, ty) = |t|^d f(x,y) per t non 0 e (x,y) non = (0,0)
Nel caso di funzioni positivamente omogenee le restrizioni alle semirette spiccate dall'origine, t(u,v) t >0 (per comodita' (u,v) stia sulla circonferenza unitaria cioe' u^2+v^2=1),
sono grafici noti di funzioni di una variabile g(t) = f(tu,tv) = t^d f(u,v), t>0, cioe' quelli della funzione potenza di esponente d, ristretta ad una semiretta, con un fattore di ``dilatazione-riflessione'' f(u,v).
In altre parole sono le funzioni che in coordinate polari (r, s) x = r cos s, y = r sin s,
dipendono dal raggio come una potenza di esso
e dall'angolo s in modo generico: f(x,y) = r^d h( s).
30-11-09 esercitazione 23 (ore 1 e 30 minuti)
- Il senato degli U.S.A. di 100 membri ha 2 rappresentanti per ognuno dei 50 stati dell'unione.
Che probabilita' c'e' che un particolare stato abbia un suo rappresentante in un comitato di 50 senatori scelti a caso?
Si puo' ragionare cosi: dato lo stato ci sono 2 senatori che lo rappresentano, due possibili successi su 50 estrazioni senza reimmissione. Si tratta quindi della distribuzione ipergeometrica (100, 2, 50)
- In un'urna vi sono 10 palline bianche e 5 nere e si fanno 3 estrazioni senza reimmissione:
a) con che probabilita non si trovano nere tra le estratte?
b) con che porbabilita' se ne trova esattamente una?
c) con che probabilita' se ne trovano almeno due nere?
Prima soluzione
per a) e b) si usa la distribuzione ipergeometrica (15,5,3)
per c) si osserva che l'evento `` almeno due nere'' e' il comp[lementare dell'evento
``o una nera o nessuna nera'' che e' l'unione disgiunta degli aventi ``una nera '' e ``nessuna nera''
quindi la probabilita' richiesta e' 1 - la somma delle probabilita' gia' calcolate ai punti a) e b).
Seconda soluzione
visto che il numero delle estrazioni e' piccolo si puo' fre un ragionamento tipo distribuzione binomiale
solo che ad ogni estrazione vi sono due possibilita' e per ciascuna di esse cambia la distribuzione di probabilita'
si indichi con n il fatto che si estrae una nera e con b che non si estrae una nera
da sinistra a destra si predispongano tante colonne quante estrazioni: 3,
si parte scrivendo nella prima colonna la probabilita' di ottenere con una estrazione una nera
quindi si divide in due casi
nella riga sopra il caso che la prima estrazione dia una nera
nella riga sotto il caso che la prima estrazione non dia una nera
quindi si va alla seconda colonna (estrazione) e si scrive in ognuno dei due casi (righe) la probabilita' di ottenere con una nuova estrazione una nera
e cosi via
n
n 3/13
b
n 4/14
n
b 4/13
b
5/15
n
n 4/13
b
b 5/14
n
b 5/13
b
si ottiene un diagramma ad albero con ``etichette'' e ``pesi'' :
per ottenere la probabilita' con cui si hanno nell'ordine certi risultati si segue il cammino delle
``etichette '' che contrassegnano i due diversi risultati e si fa il prodotto
del numero scritto prima del risulato n e di 1meno il numero scritto prima se il risultato e' b
per esempio la probabilita' di ottenere n alla prima estrazione, b alla seconda e n alla terza e'
5/15 x (1-4/14) x 4/13
ora ogni cammino rappresenta un'eventualita' disgiunta da quella di un cammino diverso
per cui la probailita' di ottenere esattamente una pallina era in tre estrazioni
sara' data dalla somma delle probabilita' di ottenere i risultai nell'ordine
(n,b,b), (b,n, b), (b,b, n).
-Grafico di f(x)= 2||x| -1|
si traccia il grafico di |x| noto lo si abbassa di 1, si ribalta la parte di ordinata negativa, lo si allunga di un fattore 2.
-Grafico di f(x)= | log (|x-1|^3) |
si usa la proprieta' dei logaritmi f(x) = 3 |log |x-1||
si traccia il grafico di log x, gli si aggiunge il suo simmetrico rispetto all'asse verticale ottenendo il grafico di log |x|, lo si sposta a destra di 1 lo si allunga di un fattore 3 mettendo in risalto questo fatto
notando che le pendenze delle retta tangenti al grafico nei punti di intersezione con l'asse orizzontale devono essre 3 e -3.
- Grafici di f(x) = log_b x (b >0 , b non = 1)
si usa la proprieta' log_b x = log x/ log b:
vari casi: 0<b<1, 1<b < e, b>e.
- Tracciare il grafico nello spazio cartesiano della funzione f(x,y) = xy/(x^2+y^2) per (x,y) non = (0,0)
Primo approccio studio degli insiemi di livello {(x,y) : xy/(x^2+y^2) =c}
si scopre che sono non vuoti se e solo se |c| , o = 1/2
infatti si tratta delle soluzioni di
x^2 - xy/c +y^2 = 0 per cui dato y vi sono uno o due x corrispondenti
x= y/2c + |y| /2|c| radq(1- 4c^2)
x= y/2c - |y| /2|c| radq(1- 4c^2)
solo se il discriminante e' non negativo.
Piu' direttamente poiche' 2xy < o = x^2+y^2 si ha sempre f(x,y) < o = 1/2.
Rimane da capire cosa sono gli insiemi del piano che hanno come elementi gli (x,y)
che soddisfano ad una delle due condizioni
x= y/2c + |y| /2|c| radq(1- 4c^2)
x= y/2c - |y| /2|c| radq(1- 4c^2)
Per far cio' e' molto piu' conveniente il secondo approccio:
la funzione f e' 0 positivamente omogenea cioe' e' costante su semirette spiccate dall'origine
(quindi le condizioni trovate definivano delle rette)
Usando le coordinate polari x = r cos s, y=r sin s si ottiene quindi anche l'interpretazione geometrica del valore costante che la funzione assume su tali semirette
f(x,y)= cos s sin s = 1/2 sin (2s).
-Tracciare il grafico di f(x)= sin (arsin x):
poiche' per definizione arsin e' l'inversa della restrizione a [-pig /2 , pig/2 ] di sin
il dominio di f e' [-1,1]
(quando si scrive arsin di qualchecosa implicitamente si sottointende la condizione che quel qualchecosa deve essere tra -1 ed 1: condizione fantasma)
poiche', d'altronde, l'immagine di una funzione inversa e' il dominio della funzione di cui si fa l'inversa
arsin ha valori tra -pig/2 e pig/2
quindi f(x)= composizione di una funzione con la sua inversa = identita' sul dominio dell'inversa =
= restrizione a [-1,1] di y=x
quindi il grafico di f e' il segmento di bisettrice tra primo e terzo quadrante con le ascisse comprese tra -1 e 1.
-Tracciare il grafico di f(x) = arsin (sin x)
- la funzione e' 2 pig periodica, basta tracciare il suo grafico su un intervallo lungo 2 pig e poi ripeterlo
-conviene considerare l'intervallo x tera - pig e pig
- la funzione e' dispari, si puo' disegnare il grafico solo per x positivo e poi rifletterlo attraverso l'origine
(0,0)
- ci si e' ridotti a disegnare il grafico di f(x)= arsin (sin x) solo per x tra o e pig
tra 0 e pig/2 f e' l'inversa di una funzione composta la funzione stessa (il seno ristretto a 0 pig/2)
quindi e' l'identita' ristretta al dominio della funzione cioe' [0, pig/2]
quindi per l'ascissa tra 0 e pig/2 il grafico di f e' il segmento di bisettrice
come procedere per x tra pig/2 e pig?
basta scrivere sin x quando x sta tra pig/2 e pig come seno di un altro argomento tra 0 e pig/2:
sin x = sin (pig - x)
e in effetti se x e' tra pig/2 e pig allora (pig - x) e' tra 0 e pig/2
quindi per x tra pig/2 e pig
f(x) = arsin (sin x) = arsin (sin (pig -x)) = essendo l'argomento nell'intervallo a cui restringo il seno per invertirlo = pig -x
quindi per l'ascissa tra pig/2 e pig il grafico di f e' il segmento di retta di inclinazione -1 passante per (pig, 0).
Quindi il grafico di f per l'ascissa tra 0 e pig e' quello di pig/2 -|x- pig/2|.
ESERCIZIO LASCIATO
tracciare il grafico di f(x)= arcos (sin x).
1-12-09 lezione 24 ( ore 2) Riferimenti: [EB] cap. 8 pagg. 202-209, 217-223 esercizi 8.1.1- 8.1.10, 8.4.1- 8.4.5.
Si ricordano le definizioni di successione di Cauchy di numeri reali e di successione convergenete di numeri reali e l'assioma di completezza di R.
sommario
PRIME NOZIONI RELATIVE AL CONCETTO DI LIMITE:
1-definizioni generali
2- la definizione di limite per funzioni tra spazi metrici, divergenza e limiti all'infinito
3- limiti di funzioni reali di variabile reale e grafici: asintoti verticali, orizzontali e obliqui
4- primi teoremi generali per maneggiare i limiti
5- la definizione di funzione continua, funzioni continue reali di variabile reale
loro grafici e teorema del valor intermedio
Cap. 1.
L'ambiente e' uno spazio metrico cioe' un insieme M con una distanza (vedere lezione 3 distanze astratte)
d: MxM --> R : d(x,y) >o = 0, d(x,y)=0 se e solo se x=y, d(x,y)=d(y,x), d(x,y) <o= d(x,z) + d(z,y)
Definizione 1 (limite di una successione a valori in un o spazio metrico).
data una successione s :N --> M si dice che essa converge ad L elemento di M se
data una soglia di errore E i valori della successione da un certo punto in poi approssimano L
per meno di E, cioe' distano da L per meno di E
precisamente
p.o. E> 0 vi e' N in N se n > N allora d(s_n, L) < E
Notazione: si scrive nel caso : s_n -->L, n-->+oo , o anche lim_{n-->+oo} s_n = L.
Osservazione: in altri termini s_n -->L vuol dire d(s_n, L) --> 0.
Definizione 2 (punto di accumulazione di un sottoinsieme A di M)
p punto di M si dice di accumulazione per A se e' approssimabile con punti di A da lui diversi
precisamente
vi e' s:N --> A per cui s_n --> p, n -->+oo, e s_n non= p per ogni n in N.
Esempi:
M= R, ]0,1[ =A, p=0: p non e' elemento di A ma e' di accumulazione per A (s_n =1/(n+2) --> 0)
M= R, A={1/(n+1); n in N }, p=1/2 e' un elemento di A ma non e' di accumulazione per A
M= R, A={1/(n+1); n in N }, p=0 non e' un elemento di A ma e' di accumulazione per A
M= R, ]0,1[ =A, p=1/2: p e' elemento di A e anche di accumulazione per A (s_n =1/2 +1/(n+3) --> 0)
Definizione 3 (palle rispetto ad un ambiente)
dato un numero r > o = 0 e un punto p di M si dice
palla chiusa in M di centro p e raggio r l'insieme dei punti di M che distano da p al piu' r
B sopralineato (p,r) = {x in M : d(x,p ) <o = r}
palla aperta in M di centro p e raggio r l'insieme dei punti di M che distano da p meno di r
B(p,r) = {x in M : d(x,p ) <r}
Definizione 4 (Intorno relativamente ad un ambiente)
sia p in M un sottoinsieme U si dice intorno di p in M
se contiene una palla in M di raggio positivo di centro p
cioe'
se esiste r>0 B(p,r) sottoinsieme di U
cioe'
se esiste r>0 per cui se d(x,p) < r allora x sta in U
Esempi:
M=R^2 U e' intorno di p=(a,b) se si trova r>0 per cui se (x-a)^2+ (y-b)^2 <r^2 allora (x,y) in U
M=R U e' intorno del numero p se si trova r>0 per cui se -r < x-p <r allora x in U
M= R, ]0,1[= U, p=0: U non e' intorno in M di 0
M=]0,1[ , ]0,1[= U, p=0: U non e' intorno in M di 0
M= R, [0,1[= U, p=0: U non e' intorno in M di 0
M=[0,1[ , [0,1[= U, p=0: U e' intorno in M di 0
M= R, ]0,1[= U, p=1/2: U e' intorno in M di p, si prende r =1/4 per esempio
M= palla unitaria centro l'origine nel piano, palla di centro (0,1) e raggio positivo, p=(0,1)
U non e' intorno in M di (0,1)
M= R, ]0,1[= U, p=1/k: U e' intorno in M di p, si prende r =1/(2k) per esempio
Definizione 5 (Aperto relativamente ad un ambiente)
un sottoinsieme A di M si dice aperto in M se e' intorno in M di ogni suo elemento
cioe' se
p.o. a in A esiste r >0 B(a,r) e' contenuto in A
Definizione 6 (Chiuso relativamente ad un ambiente)
un sottoinsieme C di M si dice chiuso in M se e' M\C e' aperto in M
Esempi:
M= R, gli intervalli senza estremi son aperti in R,
M= R, gli intervalli con tutti gli estremi son chiusi in R,
M= R, l' intervallo ]0,1] non e' ne aperto ne chiuso in R,
M=]0, +oo[, l'intervallo ]0, 1] e' chiuso in M
M arbitrario spazio con distanza: M stesso e l'insieme vuoto sono sia aperti che chiusi in M
M= R, l'insieme dei numeri irrazionali non e' ne aperto ne chiuso
M arbitrario la palla aperta e' un aperto la palla chiusa e' un chiuso
Osservazione: un insieme e' aperto se non gli appartengono i ``punti di confine'' con il suo complementare, un insieme e' chiuso se gli appartengono i punti di confine con il complementare.
In spazi pmetrci conviene per comprendere meglio introdurre la seguente nozione:
Definizione 6 bis (Chiuso per successioni relativamente ad un ambiente)
un sottoinsieme C di M si dice chiuso per successioni in M
se ogni elemento di M approssimabile con elementi di C e' lui stesso un elemento di C
cioe'
se ogni successione di elementi di C se converge converge ad un elemento di C
cioe'
per ogni (s_n)_{n in N} a valori in C
se s_n --> p elemento di M, allora p e' elemento di C
Teorema: in uno spazio metrico (M,d) un sottoinsieme e' chiuso se e solo se e' chiuso per successioni
Teorema: Unione di un numero finito di sottoinsiemi chiusi e' un sottoinsieme chiuso
Intersezione di una famiglia arbitraria di sottoinsiemi chiusi e' un sottoinsieme chiuso
Intersezione di un numero finito di sottoinsiemi aperti e' un sottoinsieme aperto
Unione di una famiglia arbitraria di sottoinsiemi aperti e' un sottoinsieme aperto
Cap. 2.
Definizione 7 (Limiti di funzioni tra spazi metrici)
data una funzione f definita su D, sottoinsieme di M con distanza d_M, a valori in N con distanza d_N
f: D ---> N
un punto b in M di accumulazione per D, ed L un elemento di N
* si dice che f tende a L per x che tende a b in D se:
approssimando b con elementi x di D da lui diversi
si puo' approssimare L con i valori f(x) e precisione arbitraria
cioe'
per ogni soglia di errore E>0 nell'immagine
vi e' una soglia di errore R>0 nel dominio per cui se
x e' in D e 0< d_M( b, x) <o= R (in particolare x non = b)
allora
d_N (L, f(x)) <o= E
in breve: p.o. E>0 es.R>0 t.c. p.o.x in D 0< d_M(x,b)< D ==> d_N (f(x) ,L) < E
In altri termini
la preimmagine di una palla centrata in L senza il suo centro L
contiene l'intersezione di D con una palla centrata in b senza il suo centro
ovvero
la preimmagine di un intorno di L ``bucato'' di L
contiene l'intersezione di D con un intorno ``bucato'' di b
Si scrivera' in tale caso f(x)---> L per x -->b in D, o lim_{x--> b, x in D} f(x) =L .
Osservazione: l'interesse di fare il limite di una funzione in un punto b e' capire come si comporta la funzione avvicinandosi al punto e non il valore nel punto b.
Il punto b potrebbe non appartenere al dominio della funzione
pur avendo la funzione limite per x che tende a b.
D'altronde la funzione potrebbe essere anche definita in b ed avere limite in b ma tali valori potrebbero essere diversi
Definizione 7 bis (limite infinito per funzioni a valori reali: divergenza)
data una funzione f definita su D, sottoinsieme di M con distanza d_M, a valori in R,
f: D ---> N
un punto b in M di accumulazione per D
*si dice che f tende a +oo per x che tende a b in D, ovvero che f diverge positivamente, se:
per ogni soglia di grandezza G nell'immagine R
vi e' una soglia di errore R>0 nel dominio per cui se
x in D e 0< dist( b, x) <o= R
allora
f(x) >o= G
in breve: p.o. G es. R>0 t.c. p.o.x in D 0<d(x,b)< R ==> f(x) > G
Si scrivera' in tale caso f(x)---> + oo per x -->b in D, o lim_{x--> b, x in D} f(x) =+oo .
Del tutto analoga la definizione di f(x) ---> -oo.
Definizione 7 ter (limite all'infinito per funzioni di variabile reale definite su insiemi illimitati)
data una funzione f definita su D, sottoinsieme di R, illimitato superiormente a valori in uno spazio metrico (N,d)
f: D ---> N
e sia L un elemento di N
*si dice che f tende a L per x che tende a +oo in D se:
per ogni soglia di errore E>0 nell'immagine
vi e' una soglia di grandezza G nel dominio per cui se
x in D e x >o= G
allora
dist (L, f(x)) <o= E
in breve: p.o. E>0 es. G t.c. p.o.x in D x>G ==> d(f(x),L) < E
Si scrivera' in tale caso f(x)---> L per x -->+oo in D o lim_{x--> +oo, x in D} f(x) = L .
Del tutto analoga la definizione di f(x) ---> L per x-->-oo.
Osservazione: in quest'ultimo caso rientra la definizione 1 di limite di una successione a valori in uno spazio metrico.
Nel caso di funzioni reali di variabile reale definite su insiemi illimitati superiormente si considera anche la seguente definizione
* Se f e' reale a variabile reale si dice che f tende a +oo per x che tende a +oo in D se:
per ogni soglia H nell'immagine
vi e' una soglia di G nel dominio per cui se
x in D e x >o= G
allora
f(x) >o= H
in breve: p.o. H es.G t.c. p.o.x in D x> G==> f(x) > H.
Si scrivera' in tale caso f(x)---> + oo per x -->+oo in D, o lim_{x--> +oo, x in D} f(x) = +oo .
Del tutto analoga le definizioni con +oo, -oo.
Osservazione: in questo caso rientra la definizione di successione di numeri divergente.
Teorema: se una funzione ammette limite tale limite e' unico.
Si considera il caso della definizione 7 essendo gli altri argomenti analoghi.
Infatti dato un limite L e un altro elemento v di N si considera E < d_N (L, v)/2:
per ipotesi si trova R per cui se 0< d_M (x, b) < R
allora d_N (f(x), L) < E
quindi per la diseguaglianza triangolare
d_N (f(x), v) > o = d_N (v,L) - d_N(f(x), L) > o = d_N(v,L) -E > d_N (v,L)/2 .
Quindi per quanto ci si avvicini a b con x da lui diverso la distanza tra f(x) e v
non potra' essere minore di d_N (v,L)/2 .
Osservazione: con un po di sforzo anche i limiti all'infinito che le divergenze possono farsi rientrare
nella nozione di limite di funzione tra spazi metrici dato con la definizione 7.
Ma non sembra nel contesto sforzo per cui valga la pena spendere altra fatica.
Piuttosto si potrebbe definire
Definizione 4 bis: (intorno di +oo, introno di -oo]
un insieme U e' intorno di +oo (-oo) in R se esiste C per cui U contiene la semiretta [C,+oo)
( (-oo, C])
cioe' se x > o = C allora x in U.
Nel caso i limiti all'infinito si recuperano traducendo la definizione 7 con la nozione di intorno.
Esempi:
-nel caso di funzioni reali di variabile reale la definizione 7 di limite e':
p.o. E>0 es.R>0 t.c. p.o.x in D 0<|x-b|< R ==> |f(x) -L| < E
cioe'
p.o. E>0 es.R>0 t.c. p.o.x in D se x diverso da b e -R< x-b< R allora -E < f(x) -L < E
- si consideri f(x) = sin x : sinx --> 0 se x-->0 infatti e' verso che |sin x| <o = |x|
(la semicorda e' piu' corta del semiarco)
quindi scelta la soglia di errore E nell'immagine sul dominio basta prendere R=E
per ottenere che se |x-0| < R si abbia |f(x) -0| <E.
- si consideri f(x) = sin 1/x : per x-->0 essa non ha limite infatti
se si considerano gli x_n del tipo 1/(2pig n), n in N, f(x_n ) = 0 --->0
se invece si considerano gli z_n del tipo 1/(pig/2 + 2pig n) f(z_n) =1 --->1
sia x_n che z_n possono essere arbitrariamenti vicini a 0 nel dominio ma i loro valori non si avvicinano allo stesso numero.
Quindi essendo il limite unico non ci puo' essere limite.
SI e' tracciato approssimativamente il grafico di sin 1/x : infinite oscillazioni tra -1 e 1 avvicinandosi x a 0: tutti i valori del segmento sull'asse verticale di ordinata tra -1 e 1 sono numeri limite di successioni di valori della funzione
- si consideri f(x)= sin 1/x : per x--->+oo sin 1/x ----> 0
infatti come sopra osservato
|sin 1/x | < 1/ |x|
quindi fissata la soglia di errore E nell'immagine se si considera la solglia di grandezza sul dominio G=1/E si ha |sin 1/x - 0| < 1/|x| < 1/G =E.
Cap. 3.
Limiti per lo studio dell'andamento grafico di funzioni reali di variabile reale:
-asintoti orizzontali:
avere limito finito L per x --> +oo significa che il grafico si avvicina sempre di piu' alla
semiretta orizzontale di quota L e di ascissa positiva {(x, L): x >0}
avere limito finito L per x --> -oo significa che il grafico si avvicina sempre di piu' alla
semiretta orizzontale di quota L e di ascissa negativa {(x, L): x <0}
-asintoti verticali
divergere positivamente (avere limite +oo) per x --> b, x< b, significa che il grafico si avvicina sempre piu' da sinistra alla semiretta verticale di ascissa b e ordinate positive {(b, y) : y>0}
divergere positivamente (avere limite +oo) per x --> b, x> b, significa che il grafico si avvicina sempre piu' da destra alla semiretta verticale di ascissa b e ordinate positive {(b, y) : y>0}
diverge negativamente (avere limite -oo) per x --> b, x< b, significa che il grafico si avvicina sempre piu' da sinistra alla semiretta verticale di ascissa b e ordinate negative {(b, y) : y<0}
divergere positivamente (avere limite -oo) per x --> b, x> b, significa che il grafico si avvicina sempre piu' da destra alla semiretta verticale di ascissa b e ordinate negative {(b, y) : y<0}
-asintoti obliqui
se una funzione f(x) e tale che [f(x) - ax - b ] ---> 0 per x--->+oo significa che il grafico di f si avvicina sempre piu' alla semiretta di ascissa positiva {(x, ax +b): x >0}
Cap. 4.
Per studiare se una funzione ha limite conviene:
cercare di ridursi a funzioni reali di una variabile reale, usare diseguaglianze e limiti noti,
usare successioni di valori della funzione (specialmet eper provare che il limite non esiste),
usare criteri di esistenza di limiti di successioni.
I criteri principi per l' esistenza di limiti per successioni di numeri reali sono:
-il postulato di Archimede : 1/n ---> 0 per n--> +oo
-il fatto che una successione sia di Cauchy: per l'assioma di completezza dovra' convergere ad un numero
da questi inoltre si deduce facilmente il seguente
Teorema: ( convergenza o divergenza delle successioni monotone di numeri)
una successione di numeri reali crescente (decrescente)
converge all'estremo superiore (inferiore) dell'insieme dei propri valori
cioe'
o diverge positivamente (negativamente) se l'immagine e' illimitata
o convrge al numero che e' estremo superiore di questa
in simboli
se x:N --> R, e x_{n+1} >o = x_n per ogni n in N allora
x_n ----> sup{ x_n : n in N}
essendo +oo tale estremo superiore se l'immagine { x_n : n in N} non e' limitata
Descrizione del teorema usando il grafico nel piano cartesiano della successione.
Per funzioni a valori in R^k ci si riduce facilmente a funzioni a valori reali
Teorema : sia f(x) = (f_1 (x), f_2(x), ... ) a valori in R^k allora
f(x) ---> L =(L_1, L_2 ...) in R^k se e solo se f_1 (x) ---> L_1 e f_2 (x) ---> L_2 ....
cioe'
una funzione a valori in R^k converge a L
se e solo se le funzioni componenti convergono alle rispettive coordinate di L
Per sincerarsene basta osservare che vale la segunete catena di diseguaglianze:
|f_i (x) - L_i | < o = | f(x) -L |_k = radq ( (f_1(x) - L_1 )^2 + (f_2(x) - L_2 )^2 +....)
e
| f(x) -L |_k = radq ( (f_1(x) - L_1 )^2 + (f_2(x) -L_2 )^2 +....) <o= |f_1 (x) - L_1 | + |f_2 (x) - L_2 | + ...
la prima diseguaglianza garantisce che se f---> L allora ogni componente converge alla rispettiva coordiata del limite,
la seconda diseguaglianza il viceversa: essendo la somma al secondo membro fatta da un numero fisso di addendi, k addendi, garantisce che se ognuo degli addendi diminuisce anche f si avvicina ad L .
In generale il seguente criterio, usato in negativo, permette, riducendosi a successioni di studiare l'eventuale non esitenza del limite e il comportamento piu' complesso della funzione
Teorema : f(x) ---> y per x --> b in D se e solo se
i valori di f lungo ogni successione di elementi di D diversi da b a lui convergente
convergono a y
cioe'
per ogni x:N--->D \{b} se x_n --> b per n-->+oo allora f(x_n) ---> y per n-->+oo
Esempi:
-si ripete l'esempio dato in precedenza:
si consideri f(x) = sin 1/x , b=0: per x-->0 essa non ha limite infatti
se si considerano gli x_n del tipo 1/(2pig n), n in N:
x_n ---> 0, x_n non= b, f(x_n ) = 0 --->0 ;
se invece si considerano gli z_n del tipo 1/(pig/2 + 2pig n):
z _n ---> 0, z_n non= b, f(z_n) =1 --->1.
- f(x)= 1/2 per x<0 ed f(x) = sin 1/x per x>0
f(x) ---> 1/2 per x<0 e x-->0
f(x) non ha limite per x>0 e x-->0
Oltre ai limiti notevoli, alle proprieta' algebriche dei limiti, al fondamentale principio di sostituzione , esposti nel seguito delle lezioni, per funzioni a valori reali lo strumento principe per il calcolo dei limiti
e' ridursi a limiti noti mediante diseguaglianze:
Definizione 4 ter [intorno bucato]
Per comodita' si dira' che una proprieta' vale in un intorno bucato di b se vi e' un intorno U di b
per cui se x sta in U ed e' diverso da b vale la prorpieta' in questione per tale x.
Teorema: (dei due carabinieri)
se g(x)--> a e h(x)-->a , x-->b e g(x) <o= f(x) <o= h(x) nell'intorno bucato di b
allora
f(x)--> a , x-->b
Chiaramente se a e' infinito basta un solo ``carabiniere'':
se a =+oo basta considerare la sola diseguaglianza g(x) <o= f(x) per ottenere la tesi,
se a= - oo basta considerare la sola diseguaglianza f(x)<o= g(x).
A parole:
se nell'intorno bucato del punto una funzione e' compresa tra due funzioni che hanno lo stesso limite allora esiste il limite di questa funzione nello stesso punto.
Esempio:
f(n) = 1/n sin^2 [ (3n^2+5 n)/( 6log n + tan n) ]
g(n)=0 --->0
h(n)= 1/n --->0
g(n)= 0 <o= f(n) <o= 1/n = h(n)
per quanto complicata f(n) e' 1/n per un valore del seno al quadrato che e' sempre
non negativo e minore di 1.
Quindi per n --> +oo, f(n) --> 0.
Una prima serie di limiti notevoli e' data dal seguente teorema sul limite all'infinito di un rapporto di polinomi
Teorema Se p(x) e q(x) sono polinomi di variabile reale, grado di p > grado di q allora
q(x)/p(x) ---> 0 per x --> +oo, -oo
Sia m il grado di p > del grado di q che si indica con n.
p(x)= b_m x^m + .... , q(x) = a_n x^n + ....
q(x)/p(x) = [a_n x^n + ....]/ [b_m x^m + ....] = si raccoglie x^n al numeratore ed x^m al denominatore
= 1/ x^{m-n} [ a_n + 1/x( ...)] / [b_m + 1/x ( ....)]
poiche' m-n >0 il primo fattore tende a 0, il secondo fattore, la frazione tende a a_n/b_m.
Il tutto tende a 0.
Cap. 5.
Consideriamo le notazioni della definizione 7:
Definizione 8 (funzione continua in un punto)
siano (M, d_M) e (N, d_N) spazi con distanza, D un sottoinsieme di M, f : D--> N ,
sia b in D e b di accumulazione per D
si dice che f e' continua (lungo D) in b se f(b) = lim_{x--> b , x in D} f(x)
Se b in D non e' di accumulazione si dira' comunque che f e' continua in b.
Definizione 8 bis (funzione continua su un insieme)
siano (M, d_M) e (N, d_N) spazi con distanza, D un sottoinsieme di M, f : D--> N ,
C sottoinsieme di D
si dice che f e' continua (lungo D) su C se e' continua in ogni punto di C
Teorema
f e' continua su C se e solo se
per ogni A aperto di N vi e' un aperto O di M per cui f^{-1} (A) = O intersecato C
(se C=M questo vuol dire che: le preimmagini di aperti sono aperti )
se e solo se
per ogni K chiuso di N vi e' un chiuso H di M per cui f^{-1} (K) = H intersecato C
(se C=M questo vuol dire che: le preimmagini di chiusi sono chiusi)
Teorema [continuita' per successioni in spazi metrici]
f e' continua in b lungo D se e solo se
per ogni successione di elementi di D se x_n ---> b si ha f(x_n) ---> f(b).
Esempio:
f(x,y)= x^2 +y^2 D=M=R^2, N=R
e' continua
| f(a,b) -f(x,y)| = | a^2- x^2 + b^2-y^2| <o= | a^2- x^2 |+ |b^2-y^2| =
= |a-x||a+x| + |b-y||b+y|
se (x,y) --->(a,b) si ha x---> a e y--> b, quindi |a-x| -->0 e |b-y|-->0.
f^{-1} ({1}) = {(x,y) : x^2+y^2= 1} e' la circonferenza untaria di centro l'origine
che risulta quindi un chiuso poiche' preimmagine di un insieme fatto
solo da un numero che e' un chiuso in R.
L'idea intuitiva di continuita' per funzioni reali di variabile reale, funzioni i cui grafici si disegnano ``senza staccare la matita dal foglio'', e contenuta bnel seguente teorema
Teorema (dei valori intermedi)
M=N=R, f continua su D , I intervallo contenuto in D allora
f(I) e' un intervallo di estremi
inf{ f(x) : x in I} e sup{ f(x) : x in I}
equivalentemente
se x e z sono in I e v e' un valore tra f(x) e f(z) allora
vi e' un punto p in I cui f(p) =v
Corollario (teorema degli zeri) l'equazione f(x)=0 ha sempre soluzione in
- ogni intervallo ove
- f sia continua e
- assuma valori sia negativi che positivi.
Si puo' dire che una funzione continua su un dominio ``tutto di un pezzo''
ha immagine ``tutta di un pezzo''.
Se si specificasse la nozione di essere `` tutto di un pezzo''
essendo il grafico di una funzione f l'immagine della funzione x-->(x,f(x)) , che nel caso risulterebbe anch'essa continua, si dedurrebbe rigorosamente che anche il grafco di f sarebbe `` tutto di un pezzo''.
3-12-09 lezione 25 (ore 1 minuti 15) Riferimenti:[EB] cap. 1 pagg. 4-7, 14-20, 26-35, cap.6 pagg. 152-162, 165-169; cap. 8 pagg. 202-217, 228-233.
Percentuali: vedere sotto esercitazione odierna.
Allineamenti decimali e serie geometriche:
L'assioma di completezza a parole: se i valori di una successione si avvicinano sempre di piu' tra loro allora si avvicinano sempre di piu' a qualche cosa.
L'assioma di completezza, i criteri di esistenza del limite come quello per le funzioni monotone da lui derivati, garantisce che ci sono i numeri di cui conosciamo solo un'approssimazione razionale, comunque definita.
Per esempio si e' definito pig essere il numero che corrisponde all'area bidimensionale del cerchio di raggio 1, essendo tale cerchio misurabile.
Per l'assioma di completezza e il postulato di Archimede si puo' dare la difinizione di misura di Peano Jordan.
Che vi sia il numero che misura l'area del cerchio si puo' vedere, meno direttamente ma piu' agevolmente, con il criterio di esistenza del limite per funzioni crescenti:
per esempio si considera la successione Sn= somma delle aree dei quadrati di lati 1/2^n contenuti nel
quarto di cerchio di raggio uno, disposti per un vertice a
partire dal centro con lati tra loro paralleli ed allineati
 e'crescente (diminuendo il lato
da 1/2^n a 1/2^(n+1) i quadrati gia'
contenuti nel cerchio si dividono in quattro, e si
aggiungono alcuni quarti di quelli che prima attraversavano la
circonferenza), e' limitata superiormente
da 1 (il quadrato di lato 2 contiene il cerchio, e il quadrato di lato
1 contiene il quarto di cerchio) quindi
converge.
e'crescente (diminuendo il lato
da 1/2^n a 1/2^(n+1) i quadrati gia'
contenuti nel cerchio si dividono in quattro, e si
aggiungono alcuni quarti di quelli che prima attraversavano la
circonferenza), e' limitata superiormente
da 1 (il quadrato di lato 2 contiene il cerchio, e il quadrato di lato
1 contiene il quarto di cerchio) quindi
converge.Il suo limite e' stato chiamato pig/4.
Si nota che pig e' cosi' ben definito ma con questo metodo non vi e' modo di sapere con una formula con un fissato numero di addizioni, moltiplicazioni divisioni, il suo valore a meno di un miliardesimo se non calcolandosi almeno S_{11}.
In altre parole, ovvero con l'approssimazione decimale di pig, piuttosto che con quella diadica sopra illustrata, si sa che
pig = 3 + 1/10 + 4/100 + ... = 3,14 ...
ma non vi e' formula con un fissato numero di addizioni, moltiplicazioni divisioni, per saper il valore della sua nona cifra ``dopo la virgola''.
In generale una qualsiasi successione di cifre in base dieci c: N ---> {0,1,2,3,4,5,6,7,8,9}
la notazione degli allineamenti decimali infiniti c0 , c1 c2 c3 ...ck.. ...
con una cifra intera ck tra 0 e 9 per ogni numero naturale k,
sta per la ``somma infinita'' c0 + c1 /10 + c2 /100 + c3 /1000 + ... + ck.. /10^k + ...
e ha senso pur senza specificare alcuna regola che permetta il calcolo della cifra al generico posto k:
c0 , c1 c2 c3 ...ck.. ... = c0 + c1 /10 + c2 /100 + c3 /1000 + ... + ck.. /10^k + ...
= lim_{n-->+oo} [ c0 + c1 /10 + c2 /100 + c3 /1000 + ... + cn. /10^n ] =
= lim_{n-->+oo} Somme per k tra 0 ed n di ck 10^{- k}
Si tratta pero' di verificare che tale limite esiste.
Serie geometriche di ragione x:
successione geometrica di ragione x e' una successione per cui il rapporto di due consecutivi e' costante ed eguale ad x
x_{n+1} = x x_n
si ha x_n = x ... n volte ...x x_0= x_0 x^n
serie geometrica di ragione x e' la successione delle somme successive dei primi termini di una successione geometrica
S_n = 1 + x + x^2 + ... + x^n
Per tali serie si riesce nel caso in cui -1< x <1 non solo a dire che hanno il limite ma a calcolarlo.
Si utilizza il prodotto notevole 1-x^n =(1-x)(1+x+x^2+...x^{n-1}) si ha
1+x+x^2+...x^n = (1-x^{n+1})/(1-x),
e se -1< x< 1 per n che aumenta x^{n+1} diventa sempre piu' piccolo e quindi per -1< x< 1
non solo ha senso la somma infinita
1+x+x^2 +... ma si sa che e' anche eguale a 1/(1-x);
Se -1< x < 1 allora esiste il limite di S_n
lim_{n-->+oo} 1 + x + x^2 + ... + x^n =
lim_{n-->+oo} Somma per k tra 0 ed n di x^{ k} = 1 /(1-x)
che si indica anche
Somma per k tra 0 ed +oo di x^{ k}
Per le serie geometriche non serve la proprieta' fondamentale dei numeri reali si sa a priori che il numero L cui si avvicinano le somme approssimanti e' 1/(1-x) !
Si usa solo il fatto che se -1< x< 1 allora x^n diventa sempre piu' piccolo (x^n < 1/n e postulato di Archimede) e la formula per 1-x^n.
Nota tale affare e' vero anche per x=-1 ma l'argomento per arrivarci e' diverso.
Per tornare agli allineamenti decimali infiniti si usa invece l'assioma di completezza per mostrare che convergono sempre mostrando che sono una successione di Cauchy:
date per ogni numero naturale n le cifre tra 0 e 9 c1, c2, c3 , ... cn considera
Mn = c1/10 + c2/100 ... + cn/10^n= 0,c1c2 c3 ... cn < o = Mk+1= Mn +cn+1 /10^(n+1)
fissa un' arbitraria soglia di errore E>0
ci si domanda se per n>h naturali abbastanza grandi E> Mn- Mh > -E, in effetti si ha
0 < o = Mn - Mh=ch+1/10^(h+1) + ... + cn/10^n < o =
9(1/10^(h+1) + ... + 1/10^n ) e questo e' il passaggio in cui dei ck si usa solo il fatto che sono tutti minori di 10
= 9/10^(h+1) (1+ ...+ 1/10^{n-h-1}) < 9/10^(h+1) 1. 1periodico= 9/10^(h+1)10/9=
= 1/10^h che e' minore di E per tutti gli h maggiori di LOG10 1/E
appunto il numero di iterazioni minimo per cui gli Mk differiscono tra loro per meno di E e' il piu' piccolo naturale n maggiore di LOG10 1/E.
Usando quindi la proprieta' fondamentale dei reali si asserisce che vi e' un numeo reale L
a cui si avvicinano sempre piu' aumentando opportunamente il numero di cifre n i numeri
0.c1c2 c3 ... cn.
Le scritture 0.c1c2 c3 ... ck... (allineamento decimale infinito) ovvero
c1/10 + c2/100 ... + ck/10^k +... (somma infinita di termini non negativi) sono sempre giustificate ed indicano (ed individuano) il numero L. Si scrivera':
L=0.c1c2 c3 ... ck... =c1/10 + c2/100 ... + ck/10^k +...
Serie: prime nozioni
data una successione f:N ---> (V, O_V, +_V, d), spazio vettoriale con distanza invariante per traslazioni e 1 positivamente omogenea, si puo' definire la successione delle successive somme dei suoi primi termini (successione delle somme parziali o serie generata dalla successione)
S_0 = f_0
S_{n+1} = S_n +f_{n+1}
cioe' usando la notazione dei ``puntini'' (che sottoindende la definizione per ricorrenza del termine (n+1)-esimo in funzione dei precedenti appena data)
S_n = f_0 + f_1 + ... + f_n
La successione generatrice della serie si dira' anche successione degli addendi o dei termini della serie (dizione quest'ultima un poco impropria in quanto porta a confondere gli F_n con gli S_n).
Quando esista il limite della successione delle somme parziali si dira' che la serie converge e il suo limite
(ancorche' non noto per via sintetica) si indichera' come somma inifinita, nell'ordine, dgli addendi della serie
lim_{n-->+oo} S_n =
lim_{n-->+oo} Somma per k tra 0 ed n di f_k =
lim_{n-->+oo} f_0 + f_1 + ... + f_n =
Somma per k tra 0 ed +oo di f_k .
Quando la successione S_n diverga si dira' che la serie diverge:
la serie geometrica di ragione 1 diverge per l'assioma di Archimede
S_0 =1, S_1 = 1 +1 =2 , ...., S_n = n.
OSSERVAZIONE: Vi sono serie, e quindi successioni che ne divergono ne convergono:
si consideri la successione f_n = (-1)^n , la successione delle sue somme parziali e'
S_0 =1, S_1 =S_0 + f_1 = 1+ (-1) =0, S_2 = S_1 + (-1)^2 = 0 +1 =1 , ...
quindi S_n assume valore 1 per n pari e 0 per n dispari.
Quindi (si veda il criterio di esistenza del limite restringendosi a successioni sul dominio) la serie non puo' convergere ne divergere, poiche' lungo due successionidi indici (elementi del dominio) che tendono a +oo, quella dei pari e quella dei dispari, si avvicina a due numeri diversi.
Si osservi che l'insieme dei valori della serie {0,1} e' un iniseme finito in particolare e' un insieme limitato
e questo e' un altro motivo sufficiente per asserire che non puo' divergere.
Una condizione generale necessaria perche' una serie converga ad un numero e' il seguente
Teorema Se la serie di addendi f_0, f_1 ... f_k, ...
cioe' se la successione S_n = f_0 + f_1 + ... + f_n
converge
allora
f_n ---> 0 per n -->+oo
Si tratta semplicemente di osservare che una successione convergente e' di Cauchy (il ``viceversa'' dell'assioma di completezza)
quindi dato E vi e' N per n>m abbastanza grandi (>N) -E < d(S_n , S_m ) = | S_n - S_m|<E
ma S_n -S_m = f_{m+1} + .... + f_n (le somme a partire dall'indice m+1 e arrivare all'indice n)
In particolare se m=n-1 si ottiene
dato E vi e' N per n > N+1 d(S_n , S_{n-1})= | f_n | < E
OSSERVAZIONE: questa condizione non e' sufficente alla convergenza della serie
come si vedra' agevolmente nel seguito del corso la serie armonica somma dei reciproci degli interi
e' divergente
somme k da 1 a +oo di 1/k = + oo
OSSERVAZIONE: ogni successione da origine ad una serie quella delle somme che hanno come addendi i valori della successione.
In particolare ogni serie e' una successione.
D'altra parte ogni successione puo' essere vista come una serie: per un'arbitraria successione
b_0, b_1 ... b_k .... e' immediata l'eguaglianza
b_n = b_ n - b_{n-1} + b_{n-1} - b_{n-2} + ... + b_2 - b_1 + b_1 -b_0 + b_0
= b_0 + somme k tra 1 e n di (b_k - b_{k-1} )
quindi ogni successione b_k e' serie della successione dei suoi incrementi successivi d_k= b_k -b_{k-1}.
Usualmente quando si scrive una successione come serie si riesce a provare piu' agevolmente che e' convergente (usando in sostanza l'assioma di completezza, cioe' provando che e' di Cauchy) senza per questo volere o poter calcolare il suo limite.
Viceversa quando una successione o serie si riesce a scrivere in forma sintetica (senza ``... '' di sorta)
di solito sara' piu' conveniente cercare di calcolare il limite direttamente.
Serie reali a termini positivi
se la successione f_0, ..., f_k una successione di numeri reali non negativi allora
la serie
S_n = f_0 +... + f_n
e' una successione crescente.
Quindi per il teorema sull'esistenza dei limiti di funzioni monotone una serie ad addendi non negativi
o converge o diverge .
Notazione scientifica (decimale):
Ogni numero reale x puo' essere scritto in modo unico
x= a 10^k con a numero reale per cui 1/10 <o= a < 1, e k numero intero
ovvero y=10 a , h= k-1
x= y 10^h con y numero reale per cui 1 <o= y < 10, e h numero intero
(y puo' essere anche maggiore di 9)
Per semplicita' (riguardo la parte intera che si usa per individuare k) lo si mostra nel caso in cui x>1:
si fa il logaritmo in base 10 di x
Log x
si pone h = parte intera di Log x = piu' grande intero minore o eguale a Log x
si pone b = parte decimale di Log x =Log x - h, per definizione di parte intera 0 <o= b < 1
si ha chiaramente Log x = Log x - h + h = b + h
si fa l'esponenziale in base 10 ottenendo
x = 10^b 10^h
si pone y = 10^b e si ha per quanto detto 1<o= y <10.
Quindi k= 1+ parte intera di Log x e a = 10^{parte decimale di Log x - 1}.
Tasso di interesse composto, decadimento radioattivo, diseguaglianze tra medie aritmetiche e medie geometriche, costante di Nepero:
Per i dettagli si leggano gli appunti di questo collegamento .
In breve
Teorema
La media geometrica di n numeri non negativi e' minore o eguale alla media aritmetica.
Per le idee di fondo si veda l'esercitazione sotto.
OSSERVAZIONE: questa diseguaglianza passando ai logaritmi in base maggiore di 1 dice che le funzioni logaritmo sono concave (cioe' la funzione - logaritmo in base maggiore di 1 di x e' convessa).
Teorema
La successione del tasso di interesse composto x,
x_n= ( 1+ x/n )^n, per i naturali maggiori di -x e' crescente: x_{n+1} > x_n se n>-x.
Essendo inoltre limitata superiormente si ha:
Teorema
La successione del tasso di interesse composto x, ( 1+ x/n )^n e' convergente per n-->+oo.
Definizione :[Costante di Nepero] Il limite della successione ( 1+ 1/n )^n si denota con e .
Teorema (non dimostrato) lim_{n-->+oo} ( 1+ x/n )^n = e^x per ogni x in R.
anzi diro' di piu'
Teorema (ancora da enunciare a lezione) lim_{n-->+oo} ( 1+ z/n )^n = e^z per ogni z in C.
OSSERVAZIONE:
usando la formula del binomio di Newton ( 1+ z/n )^n e' il polinomio nella variabile z di grado n
somme per k da 0 a n di binomiale n su k (1/n)^k z^k
OSSERVAZIONE : (1+ 1/n )^n < e < (1+ 1/n )^{n+1} vedi appunti.
3-12-09 esercitazione 24 (minuti 45)
Diseguaglianza tra medie geometriche ed aritmetiche di 2, 4, 3 numeri non negativi
per 2 numeri non negativi il doppio prodotto delle radici e' piu' piccolo della somma dei numeri perche' questa e' la somma dei quadrati delle radici: quindi si ha quanto voluto per due numeri; vedendo la radice quarta del prodotto di 4 numeri come la radice quadrata del prodotto delle due radici quadrate di copiie dei quattro fattori si applica quanto appena provato per due numeri una prima volta ottenendo che la radice quarta e' piu' piccola della media delle due radici quadrate, quindi lo si applica ancora ad ognuna delle radici quadrate: si e' provato quanto voluto per quattro numeri, e con lo stesso metodo lo si prova per 2^n numeri; per provarlo per 3 numeri si va all'indietro: si fa il prodotto di questi 3 numeri con la loro media aritmetica, e si applica a questi quattro fattori la diseguaglianza provata elevata alla 4, nella frazione ottenuta si semplifica, quindi si dividono i membri della diseguaglianza per la medi dei tre numeri iniziali ed estraendop la radice cubica ad ambo i membri si ottine la diseguaglianza agognata:e metodo analogo lo si usa in generale per passare dalla diseguaglianza vera per n+1 numeri a quella vera per n numeri
Percentuali e serie geometriche
Esercizio n. 7 sezione A del recupero della prima prova initinere del 10/11/2008.
Due colonie batteriche equinumerose hanno un incremento del 10% rispettivamente in 2 e 4 ore.
In quanto tempo la popolazione totale aumenta del 25%?
Esercizio n. 3 sezione A del recupero della prima prova initinere del 10/11/2008.
Una cisterna contiene inizialmente 3400 l d'acqua. Si stima che nel corso di una settimana venga prelevato l'85% del suo contenuto; alla fine di ogni settimana la cisterna viene rifornita di altri 3400 l d'acqua. Nel corso dei mesi la quantita' d'acqua presente nella cisterna non puo' aumentare oltre un certo valore.Quale?
10-12-09 PRIMA PROVA IN ITINERE (ore 2 minuti 30)
I testi della prima prova in itinere.
Le soluzionidella prima prova in itinere.
14-12-09 lezione 26 (ore 2)
Cenni di statistica descrittiva e parallelo con nozioni di calcolo delle probabilita'
Primi termini di statistica descrittiva
Caratteri
si intendo le caratteristiche che interessano e che sono soggette a osservazione
e si possono far corrispondere nell'ambito astratto delle funzioni agli elementi del codominio
relativamente al contesto dell'osservazione si puo' preliminarmente distinguere i caratteri
in tre famiglie:
non quantitativi (e.g. se si osservano comportamenti di soggetti diversi) che vengono denotati
in modo piu' o meno arbitrario: si e' a livello di scala nominale ovvero di semplice classificazione
ordinabili, grosso modo caratteristiche anche non numeriche che hanno significativamente, per la comunita' interessata all'osservazione, un ordine: si parla di scala ordinale, se poi vi e' un significato
intrinseco degli intervalli, come nella scala centigrada delle temperature dove un intervallo di 1 grado in condizioni fissate ha significato fisico ben preciso, si parla di scala d'intervallo
quantitativi, per tali caratteristiche, scalari o vettoriali che siano, ha significato intrinseco e rilevante il rapporto ovvero il confronto quantitativo fra due di esse, per esempio la scala Kelvin delle temperature
ove si misura in sostanza un energia cinetica e si fissa un'origine; si parla di scala razionale
chiaramente in tale classificazione (tipicamente nominale!) possono sorgere ambiguita': per esempio volendo osservare direzioni piane si e' senza dubbio in ambito di scala di intervallo, e si puo' discutere se, non avendo una direzione di riferimento ``assoluta'' si sia nell'ambito di una scala razionale o meno, in quanto ha senza dubbio senso intrinseco asserire che l'angolo tra due direzioni e' il triplo dell'angolo tra altre due direzioni.
Popolazione
e' l'insieme M dei ``soggetti oggetto'' di osservazione relativamente ai caratteri che interessano,
tipicamente come sono distribuiti i caratteri sull'intera popolazione e' l'incognita di cui si interessa
il successivo capitolo della statistica (la statistica inferenziale) che verra' trattata solo marginalmente nel presente corso.
Campione
e' l' osservazione dei caratteri di interesse su un certo numero di soggetti della popolazione.
Un campione unitario puo' essere utilmente visto, come sara' ribadito piu' sotto, come funzione che abbia come dominio la popolazione M e codominio l'insieme C dei caratteri.
Per un campione con n soggetti si puo' pensare ad un'estrazione con o senza rimpiazzo.
Nella pratica della statistica, in molti casi, per le valutazioni che interessano, e' sempre possibile l'approssimazione con estrazioni con rimpiazzo.
Tipicamente il campione di n elementi viene indicato con x_1, x_2 ...x_n .
E' chiaro che di solito questa numerazione dei valori del campione non e' detto si a significativa: indica solo un modo di mettere in ordine i dati quando non vi si per se un ordinamento significativo.
Nel caso sia lecito approssimare il campione come estrazione con rimpiazzo un campione di n elementi e' determinato da una funzione da M a valori in C^n. Equivalentemente, volendo parafrasare la procedura ``scelti con rimpiazzo n elementi di M si osserva il carattere posseduto'' la composizione di una funzione k: {1, ...n} --> M con una funzione x:M-->C: x_k(i), determina un campione.
Prime nozioni corrispondenti in calcolo delle probabilita'
A)
Prima di iniziare questo parallelo conviene estendere la nozione di probabilita' , come in uso nella comunita' matematica, in vista del fatto che possono essere utili dei passaggi al limite per ricondursi a probabilita' di eventi piu' elementari.
Per esemplificare: se si misurano con errore altezze ogni singola misura e' ragionevolmente individuata da un intervallo di numeri reali (stima massima stima minima), percio' interessano le ``asserzioni atomiche'': ``con che probabilita' quanto misurato e' piu' piccolo di b a piu' grande di a'' ovvero ``con che probabilita' quanto misurato sta in ]a,b[''.
La singola misurazione si puo' far corrispondere a una funzione X di dominio M magari incognito ed a valori reali: una misura dell'insieme {p in M : X (p) in ]a,b[} brevemente indicato con {X in ]a,b[} dara' la probabilita'.
Idealmente si potrebbe avere una successione infinita di tali misure, quindi di tali intervalli, e le proposizioni che interessano per questa ipotetica successione di osservazioni oltre a quelle esprimibili
dalla combinazione con negazione, congiunzione, o disgiunzione delle asserzioni atomiche (che corrispondono alle asserzioni relative alle unioni o intersezioni finite e al complementare di intervalli) quelle espresse anche con ``per ogni ed esiste'' , relativamente alla successione in oggetto, che corrispondono alle unioni o intersezioni di successioni di intervalli:
per esempio l'asserto
la probabilita' che la successione di misure X_1, X_2 ... converga ad un numero L e' minore di 1/3
cioe'
la probabilita' che per ogni k in N vi sia n in N per ogni m maggiore di n per cui L-1/k < X_m <L +1/k e' minore di 1/3
corrisponde
P({ m in M: per ogni k in N esiste n in N per ogni m>n per cui L-1/k < x_m <L +1/k}) <1/3
cioe'
P(Intersezionek in N Un in N Intersezione m > n {p in M: X_m (p) in ]L-1/k , L+1/k[ }) < 1/3
Rimarrebbe come ultimo passaggio quello di ``tirar fuori dalla probabilita' '' le unioni ed intersezioni
infinite riconducendosi a vari limiti iterati delle probabilita' ``elementari''
P( { X_m in ]L-1/k , L+1/k[ }) .
Per far cio', appunto, si devono estendere le definizioni di algebra, di misura matematica e di probabilita' date nelle lezioni n.6 del 13-10-09, n.10 del 26-10-09, n. 19 del 19-11-09.
Sigma-algebra di insiemi: un insieme M di sottoinsiemi di M si dice sigma-algebra se
A) tutto M sta in M
B) se A e B stanno in M allora anche la loro differenza sta in M
C) se A_1, A_2 , A_3 ... e' una successione di sottoinsiemi elementi di M allora anche l' unione Ui in N Ai , e l'intersezione Intersezionei in N Ai stanno in M
(In altre parole e' un algebra che contiene anche le unioni e intersezioni di successioni di suoi elementi).
Probabilita' e misure sigma-additive: una misura m numerabilmente additiva su un insieme X e' quindi una funzione con dominio una sigma-algebra M di sottoinsiemi di X per cui valgono:
1) m(A) e' un numero reale non negativo
2) m(vuoto)=0
3) m(AUB) =m(A) +m(B)- m(A intersezione B)
di conseguenza
3)bis se A_1, A_2 , A_3 ... e' una successione di sottoinsiemi elementi di M allora
m(Ui in N Ai ) <o= m(A_1 ) + m(A_2 )+ ... = lim_{n -->+oo} m(A_1 ) + ... + m(A_n )
4) se A e' contenuto in B si ha m(A) =o< m(B)
m: M --> [0,+oo]
In particolare una probabilita' (numerabilmente additiva) P su un insieme X puo' essere definita
come una funzione con dominio una sigma-algebra A di sottoinsiemi di X, che e' una misura per cui
5) P(X)=1
P: A ---> [0;1]
Ecco le regole del calcolo delle probabilita' utili per ``tirar fuori'' unioni ed intersezioni numerabili
e ridusi al calcolo di limiti:
Teorema se P e' una probabilita' numerabilmente additiva allora
- se A_1, A_2 , A_3 ... e' una successione di sottoinsiemi disgiunti elementi di M allora
P(Ui in N Ai ) = P(A_1 ) + P(A_2 )+ ...
- se B_1, B_2, B_3 ... e' una successione di sottoinsiemi elementi di M crescente rispetto all'inclusione allora
P(Ui in N Bi ) = lim_{i -->+oo} P(B_i )
- se B_1, B_2, B_3 ... e' una successione di sottoinsiemi elementi di M decrescente rispetto all'inclusione allora
P(Intersezionei in N Bi ) = lim_{i -->+oo} P(B_i )
La dimostrazione del primo punto e' cosi:
da 3) ripetuto si ha per ogni n
P(A_1 ) + P( A_2 ) + ...+P( A_n) = P(A_1 U A_2 ...U A_n)
da 4)
e' minore eguale a P(Ui in N Ai )
da 3) bis e' minore eguale a P(A_1 ) + P(A_2 )+ ... . Quindi per ogni n
P(A_1 ) + P( A_2 ) + ...+P( A_n) <o= P(Ui in N Ai ) <o= lim_{n -->+oo} P(A_1 ) + ... + P(A_n )
quindi facendo il limite per n -->+oo il primo membro converge al terzo mebro della catena di diseguaglianze.
Il secondo punto si prova considerando A_1 = B_1 e per i successivi A_i= B_i \ B_{i-1} ed usando quanto provato.
Per il terzo punto si usa il secondo, passando ai complementari grazie alle leggi di De Morgane alla 3).
B)
Cio' detto il parallelo con i concetti di statistica e' il seguente
Spazio misurabile: la coppia (M, M) ove M sia una sigma-algebra su M
Spazio di probabilita': il dato (M, P, M) ove M sia una sigma-algebra su M e P una probabilita' di dominio M
usualmente incognito corrisponde grosso modo al concetto di popolazione introdotto e P ad una ipotetica valutazione su tale popolazione di tutte le possibili distribuzioni di caratteri su di essa, compatibili con la sigma-algebra data.
Funzione misurabile: dati due spazi misurabili (M, M) e (C,F)
una funzione X:M-->C si dice misurabile se
la preimmagine mediante X di un sottoinsieme elemento di F e' sottoinsieme elemento di M
ovvero
se F in F allora X^{-1}(F) in M
se F in F allora {p in M: X(p) in F} in M
Notazione: invece di {p in M: X(p) in F} quando non vi sono ambiguita' si usa {X in F}.
la funzione misurabile corrisponde quindi ad un campione unitario sulla popolazione incognita in oggetto.
Per esemplificare:
-si tenga presente che (M, M) e' usualmente incognito e ha importanza per esprimere con il linguaggio delle funzioni (matematicamente rigoroso e con regole ben precise per fare deduzioni) il concetto intuitivo che ``X sia un carattere aleatorio'';
-usualmente si parte da un sottoinsieme di eventi interessanti H famiglia di sottoinsimi di C
(per esempio nel caso di una misura aletaoria di altezze C sara' la semiretta [0;+oo[, H sara' l'insieme di tutti gli intervalli della semiretta non negativa (con estremi razionali))
-quindi F sara' la piu' piccola sigma-algebra contenente H
-le regole del calcolo delle probabilita' permettono conoscendo solo i valori di P({X in H}) quando H e' in H di dedurre i valori di P({ X in F}) per F in F
-nella pratica (non matematica) la sigma-algebra M e' sottointesa essendo proprio quella delle preimmagini di elementi di F : cioe' degli insiemi { X in F} per F in F
-la conoscenza completa di P({ X in F}) corrisponderebbe quindi alla soluzione di uno dei principali problemi di statistica
OSSERVAZIONE: quando la popolazione e' finita e conosciuta in molti casi e' spontaneo, anche se non ce ne accorge, che si modellizzi la situazione considerando M=C, M=F= insieme di tutti i sottoinsiemi di C
X la funzione identita'. Si pensi al lancio di un dado: lo spazio di probailita' coincide con lo spazio dei possibili risultati {1,2,3,4,5,6} e gli eventi interessanti son tutti i sottoinsiemi non vuoti di {1,2,3,4,5,6}.
Nel caso di dado non truccato a priori la probailita' sara' un dato : numero di casi favorevoli diviso numero casi possibili.
Invece in casi piu' complicati per esempio quando X e' una misura, anche con precisione infinita e non affetta da errore, di altezza sulla popolazione italiana, che pur sempre e' un insieme finito, conviene
proprio per dedurre come sono distrubuite le altezze sull'intera popolazione pensare la singola misura come variabile aleatoria. Quindi dal campione , di solito molto meno numeroso della popolazione, dedurre
stime di tale distribuzione. A maggior ragione questa impostazione e' utile quando le misure sono affette da errori intrinseci di carattere a sua volta casuale dovuti a cause molteplci e singolarmente non rilevanti o non apprezzabili quantitativamente in maniera effettiva.
OSSERVAZIONE: un campione unitario per testare la distribuzione di certi caratteri C su una popolazione M puo' quindi esser visto come funzione misurabile da M in (C , F), ove F sara' la sigma -algebra generata dalle combinazioni che interessano dei caratteri.
Sigma-algebra di Borel: e' la piu' piccola sigma-algebra su R^n o C^n contenente le palle della distanza euclidea, ovvero gli aperti. Si indica con B(R^n) o B(C^n).
Variabile aleatoria: e' una funzione misurabile da uno spazio misurabile rispetto a
(R^n, B(R^n) ) o (C^n,B(C^n))
Frequenze
Si indica come uso con #A il umero di elementi di un insieme A.
Consideriamo un campione di n elementi , x_1 ...x_n, per dei caratteri C, e sia v in C
frequenza assoluta di v = numero di elementi del campione che assume il valore v
=#{ k : x_k =v}
frequenza relativa di v =1/n frequenza assoluta di v
Diagramma di frequenze
Vi sono diversi modi di rappresentare la distribuzione dei caratteri di un campione.
Uno in particolare consiste nel rappresentare i caratteri assunti o rilevanti per il campione
con i punti iniziali di intervalli non sovrapposti su di un asse orizzontale, quindi mettere in evidenza sull'intervallo di ogni carattere una colonna verticale di altezza (od area se gli intervalli di base sono eguali) proporzionale alla frequenza del carattere.
Rappresentando invece i caratteri che interessano solo con punti, magari equidistanti, sull'asse orizzontale e traccianto sopra ognuno di essi un segmento di altezza proporzionale alla sua frequenza si ottiene un altro tipo di diagamma (a barre) per le frequenze.
Si nota che in un diagramma di frequenze puo' capitare che i caratteri ammissibili ma non interessanti per il campione non siano rappresentati.
Diagramma cumulativo di frequenze
Ha senso quando i caratteri siano in scala ordinale.
Si ottiene dal diagramma delle frequanze giustapponendo ad una colonna tutte le colonne precedenti:
si ottiene cosi una scala in cui l'altezza dei gradini e' proporzionale a quanti elementi del campione non sono maggiori del carattere rappresentato dalla base del gradino.
Funzione di distribuzione
E' la funzione che ad un possibile carattere associa la sua frequenza relativa.
Se C e' l'iniseme dei caratteri (il codominio del campione) il dominio della funzione di distribuzione e' C
f(v) =1/n #{ i : x_i =v}, f: C ---> R
Quando tutti i caratteri di C siano effettivamente intressanti per il campione, e quindi riportati nel diagramma di frequenze, il diagramma delle frequenze a barre determina il grafico della funzione di distribuzione : i punti del piano che hanno come ascissa il carattere e ordinata la sua frequenza relativa.
Funzione di ripartizione (scala ordinale)
F(v) = 1/n # { i : x_i < o = v}, F: C ---> R
Anche in questo caso vi e' un collegamento tra diagramma cumulativo dell frequenze e grafico della funzione di ripartizione.
Particolarmente significativo e' quando C e' un sottoinsieme finito o una successione in R:
nel caso il grafico di F e' una scala che ha un gradino in corrispondenza di ogni carattere assunto dal campione
tale grafico da proprio il diagramma cumulativo delle frequenze.
Moda (scala nominale)
La moda in un campione e' il carattere con frequenza assoluta maggiore.
Quantili e mediane (scala ordinale)
Avendo un campione in scala ordinale si puo' parlare piu' propriamente di mediane:
se il campione e' dispari la mediana e' il valore del campione che `` divide in due il campione'': meta' dei caratteri del campione non e' maggiore e l'altra meta' non e' minore
se il campione e' pari conviene parlare di valori mediani e sono i due valori del campione che lo dividono in due:
per cui meta' del campione non e' maggiore del minimo di quei valori e meta' non e' maggiore
del massimo di quei valori
in formule:
dato il campione ordinato secondo gli indici x_1 , x_2 .... x_n
se n =2 m e' un numero pari
mediane = {x_m , x_{m+1}}
se n= 2m +1
mediana = x_{m+1}
Nel caso in cui il campione sia non solo in scala ordinale ma anche rapportale
quando n = 2m e' pari come mediana si prende il valor medio delle mediane
1/2 ( x_m + x_{m+1})
Quantili e percentili: intuitivamente il quantile di proporzione q < 1 e' dato dai valori del campione per cui prima di essi vi siano almeno qn valori
in formule
se nq e' un numero naurale
q- quantili = { x_qn , x_{qn+1}}
se nq non e' un numer naturale
q-quantile = x_{ parte intera di qn + 1}
La mediana e un quantile di proporzione 1/2.
Analogamente alla mediana quando abbia senso e' convenzione prendere come q- quantile nel caso in cui qn sia intero la media aritmnetica dei due quantili.
Estensione dei concetti al calcolo delle probabilita'
Come osservato, lezione 10 del 26-10-09, la nozione stessa di probabilita' si fonda ed astrae quello di frequenza relativa.
Funzione di distribuzione per funzioni misurabili con immagine numerabile o finita
Per una generica funzione misurabile X tra (M, M, P) e (C,F) la nozione di funzione distribuzione
puo' essere fuorviante
f(v) = P( {X=v} ), f: C --> R
in effetti f(v) potrebbe essere sempre nulla.
(Per porre rimedio a cio', almeno nel caso di variabili aleatorie, una volta introdotti gli integrali converra' parlare di funzione di densita' g(v), e di misura di distribuzione piu' che di funzione di distribuzione definita come integrale di questa :
m(B) = integrale su B di g(v) dv.
Intuitivamente nel caso la funzione di distribuzione sarebbe sempre infinitesima f(v)= g(v) dv).
Questa nozione di funzione di distribuzione ha ancora senso, e descrive completamente la situazione, quando con probabilita' 1 l'immagine della funzione X sia finita o sia una successione v_1, v_2 ...
infatti poiche' {X in C} = M dovra' essere per le proprieta' della probabilita'
P({X in C}) =1
inoltre poiche' per ipotesi P({X in C}) = P( {X= v_1} U {X= v_2} U ... )= serie per n da 1 a +oo P((X=v_n})
si deve avere
1= lim_{n-->+oo} P((X=v_1}) + ... + P((X=v_n})
e quindi non tutti gli addendi possono essere nulli (senno' il limite sarebbe nullo).
Funzione di ripartizione per variabili aleatorie reali
Per una variabile aleatoria reale X:M --> R , C= R, l'estensione del concetto di funzione di ripartizione, sostituendo le frequenze con le probabilita', invece descrive ancora completamente la situazione
F(v) = P({X < o = v }) = P ({ X in ]-oo, v]})
Per le proprieta' delle probabilita' si ha
a) 0 < o = F < o = 1
b) F e' una funzione non decrescente
c) F e' una funzione continua da destra cioe' lim_ {x--> v, quando x >v} F(x) = F(v)
(si tralascia il cenno di dimostrazione esposto a lezione)
quindi il suo e' un grafico che:
a') sta sopra l'asse delle ascisse e sotto la retta orizzontale di quota 1
b') cresce con eventuali tratti orizzontali
(corrispondenti ad intervalli di caratteri, sull'asse delle ascisse, in cui X capita con probabilita' nulla)
c') puo' avere dei salti e il valore nel punto di salto e' l'estremo superiore dell'intervallo verticale di salto
Si puo' inoltre provare che i punti di salto sono al piu' una successione.
Si nota inoltra che se la funzione di ripartizione e' continua necessariamente la funzione di distribuzione
e' nulla, e quindi non significativa:
f(v) = P({X=v}) = P ( { X < o = v} intersecato Intersezione_n { X > v - 1/n}) =
= P ( Intersezione_ n [{ X < o = v} \{X < o = v - 1/n}]) = (itersezione decrescente)
= lim_{n--> +oo} P ( { X < o = v} \{X < o = v - 1/n}) =
= lim_{n--> +oo} P ( { X < o = v}) - P({X < o = v - 1/n}) =
= lim_{n--> +oo} F(v) - F( v - 1/n) = 0
Mediana per variabili aleatorie con ripartizione continua e strettamente crescenteE
Se X variabile aleatoria reale ha funzione di distribuzione continua strettamente si estende in maniera suggestiva e diretta il concetto di mediana a partire dal grafico della funzione di ripartizione:
la mediana e' l'unico valore sull'asse orizzontale in cui la funzione di ripartizione vale 1/2
quindi la mediana si trova dal grafico di una funzione di ripartizione strettamente crescente e continua
tracciando la retta orizzontale di quota 1/2 e prendendo l'ascissa del punto di intersezione di tale retta con il grafico di questa funzione di ripartizione.
Esercizio svolto: dato un diagramma cumulativo di frequenze come individuare le mediane
Esercizio lasciato: dato un diagramma di frequenze come individuare le mediane
15-12-09 lezione 27 (ore 1)
Ripetizione dei principali concetti della precedente lezione.
Media di un campione
Dato un campione quantitativo su n soggetti: x_1, ... , x_n posto x=(x_1, ... , x_n)
si definisce la media
m(x) =<x> = 1/n (x_1 +... + x_n)
Si osserva che se i caratteri sono vettoriali ( x_1 = (x_1^1, ... , x_1^k) , ... x_n = (x_n^1, ..., x_n^k))
la media sara il vettore avente come k componenti le omologhe medie delle componenti.
Media pesata: espressione della media con i caratteri
<x> = somma sui valori v di v frequenza relativa di v
Media pesata: baricentro di masse con posizione i vettori di cui si fa la media con pesi la massa nel punto individuato dal vettore diviso la massa totale
15-12-09 esercitazione 25 (ore 1)
Esercizi su moda, mediana, media.
Esercizio 12 III prova in itinere del 19/12/08 corso di Matematica e Statistica per Scienze Ecologiche anno accademico 2008-09 Tortorelli. Testo Soluzione
Esercizio 4 del 4 foglio di esercizi del 12/11/2008 corso di Matematica e Statistica per Scienze Biologiche anno accademico 2008-09 Alberti:
data la tabella di otto corsi
crediti per corso 12 , 3, 9, 6, 6, 6, 6, 12
studenti che superano 19, 85, 36, 59, 29, 47, 31, 33
l'esame del corso
calcolare media e mediana del numero di crediti per esame
calcolare il numero medio di esami per studente
e' possibile calcolare la mediana dl numero di esami per studente?
17-12-09 lezione 28 (ore 1 minuiti 30 ) cfr. 15-10-09 lezione 7
Media di una variabile aleatoria con immagine una successione
Dall'espressione della media con i caratteri e le loro frequenze relative si estende facilmente questa nozione dal caso di campioni a quello di variabili aleatorie:
se X e' una variabile aleatoria per cui P({X=v_1 o X=v_2 o ... })=1 si definisce
media di X, detto anche valore atteso o speranza matematica il valore
serie_n v_n P({X=v_n}) = lim_{n-->+oo} v_1 P({X=v_1}) + ... + v_n P({X=v_n})
(nelle ipotesi in cui la serie dei moduli sia finita
lim_{n-->+oo} |v_1| P({X=v_1}) + ... + |v_n| P({X=v_n} < +oo)
esso si indica con: m(X) o <X> o E(X).
NOTA: il parallelo tra campioni e variabili aleatorie, ovvero tra frequenze relative e probabilita', e' profondamento giustificato da alcuni teoremi di calcolo delle probabilita' che asseriscono che campioni sempre piu' numerosi su una popolazione hanno medie campionarie che convergono ``in probabilita'' alla media sull'intera popolazione.
Proprieta' della media
Linearita'
se x ed y sono due campioni o variabili aleatorie ed a, b due numeri reali
m(ax +by) = a m(x) +b m(y)
Ancora minimi quadrati: proprieta' di minimalita' della media
la media di x=(x_1, ... x_n) e' il numero c che rende minima la somma dei quadrati degli errori
E(c) = |x_1 -c|^2 + ... + |x_n -c|^2 infatti si puo' usare il metodo di quadratura
E(c) = (x - (c,...,c)) . (x - (c,...,c))
= |(c,...c)|^2 - 2 x . (c,..., c) + |x|^2 =
= nc^2 - 2c somme x_i + |x|^2 =
= (radq (n) c - 1/radq (n) somme x_i )^2 + |x|^2 - (somme x_i)^2/n
che 'e minimo quando c = 1/n somme x_i.
Campioni e variabili aleatorie centrate
Si dice campione centrato dal campione (x_1, ... x_n)
il campione (x_1 -m(x), ..., x_n -m(x))
Analogamente se X e ' una var. al. la si centra considerando la var. al. X-<X> .
Chiaramente un campione centrato ha media nulla.
Varianza e deviazione standard
Il valore minimo di E(c), che si ottiene con c = media, si chiama varianza
Var(x) = 1/n somme (x_i - m(x))^2 = 1/n | x- (<x>, ...<x>)|^2 =1/n( x- (<x>, ...<x>)). ( x- (<x>, ...<x>))
Var (x) = somme (v-m(x))^2 frequenza relativa di v
la deviazione standard e' la radice quadrata della varianza (usualamente indicata con sigma)
Si ha anche la seguente espressione dalle proprieta' del prodotto scalare
Var (x) = 1/n somme x_i^2 - (1/n somme x_i )^2 = media dei quadrati - quadrato della media
Proprieta'
-la varianza e' una quantita' che amplifica le distanze dalla media maggiori di 1 e smorza quelle minori di 1
-se si aggiunge la stessa costante al campione la varianza non cambia
Var (x + (a, ..., a)) = Var (x)
-se si moltiplica il campione per un fattore numerico b la varianza
Var (bx) = b^2 Var (x)
-se si hanno due campioni x=(x_1, .. x_n), y=(y_1,... y_n)
Var (x+y) = Var (x) + Var (y) + 2 /n (x - (<x>,...<x>)).(y - (<y>,...<y>))
Covarianza
Dati due campioni x ed y ``l'errore di additivita' nella varianza '' si dice covarianza
Cov (x,y) = 1/ n somme (x_i -m(x)) (y_i - m(y)) = 1/n (x - (<x>,...<x>)).(y - (<y>,...<y>))
= .... = 1/n somme x_i y_i - m(x)m(y)
= 1/n |x - (<x>,...<x>)| |y - (<y>,...<y>)| cos (x- (<x>,...<x>)) O (y-(<y>,...<y>))
Essendo le medie lineari la covarianza e bilineare cioe' separatamente lineare in ognuno dei due campioni.
Correlazione
Corr(x,y) = Cov (x,y) / sigma(x) sigma (y) = cos xOy
quindi la correlazione e' sempre tra -1 ed 1
inoltre la correlazione e' massima in modulo se e solo se visto che e' un coseno, i due vettori dati dai campionoi centrati, sono allineati con l'origine, cioe' per qualche numero b :
b (x_1-m(x) , ..., x_n -m(x))= (y_1-m(y), ... , y_n - m(y)) cioe'
bx_1 + m(y) -b m(x) = y_1
.
.
.
bx_n + m(y) -b m(x) = y_n
questo vuol dire considerando i dati, x =(x_1 ...x_n ) e y= (y_1 ...y_n) , non come coppia di vettori in R^n
ma come n punti in R^2 (x_1, y_1), .... (x_n, y_n)
che questi n punti giaccionno tutti sulla stessa retta di equazione
bX + m(y) -b m(x)= Y
Quindi la massima correlazione in modulo e' equivalente a una dipendenza lineare tra i due campioni.
Volendo sondare altri tipi di dipendenza quando la correlazione si ainvece picoola
per dipendenze del tipo
Y= a^X b si sonda la correlazione lineare tra x_1 ... x_n e log (y_1 +c) .... log (y_n +c)
scala logaritmica
Y= X^a b si sonda la correlazione lineare tra log (x_1 +d) .... e log (y_1 +c) ...
Varianza, covarianza: estensione del concetto a variabili aleatorie aventi con probabilita' 1 immagine una successione (quando le varianze siano finite).
Retta di regressione e metodo dei minimi quadrati
Considerando due campioni su n soggetti come le coordinate di n puntio nel piano
(x_1, y_1), ... (x_n , y_n) , e per motivi non matematici volendo considerare i dati espressi dalle y_1 ...
come dipendenti da quelli espressi dalle x_1 ..., avendo un coefficiente di correlazione abbastanza grande in modulo si chiede una retta che ``meglio'' si adatti a passare in mezzo agli n punti cosi individuati.
Un criterio per determinare questo ``meglio'' e quello di rendere minima la somma dei quadrati delle differenze delle ordinate dei dati con il valore sulla retta che danno leascisse dei dati, graficamente
la somma dei quadrati delle lunghezze dei sementi verticali che congiungo un punto tra quelli dati e la retta:
quindi la retta Y+=aX + b che si sceglie e' quella i cui coefficienti rendeno minima
E(a,b) = somme_i (a x_i + b -y_i)^2
Dal puno di vista geometrico e matematico non dovendo privilegiare una variabile rispetto ad un altra si potrebbe invece chiedere di render minima la somma dei quadrati delle distanze degli n punti dalla retta e conisderare rette in forma generale aX+bY= c.
17-12-09 esercitazione 26 (minuti 30)
Fine della discussione dell'esercizio 4 : perche' non e' possibile con i dati forniti determinare i valori mediani.
Esercizi lasciati
- Trovare una distribuzione compatibile con i dati dell'esercizio 4 e mediana {2,3}
- Quali sono i possibili valori di mediana compatibili con i dati dell'esercizio 4?
- Quante sono le distribuzioni compatibili di date mediane??
11-1-10 lezione 29
Ripetizione delle principali proprieta' della media, della varianza e della covarianza, e loro estenzione al caso di variabli aleatorie che abbiano con probabiloita' 1 immagine una successione.
Calcolo con i minimi quadrati della retta di regressione
Per rendere minima
E(a,b) = somme_i ( a x_i +b - y_i )^2
conviene lavorare con campioni centrati
E(a,b) = somme_i ( a (x_i -m(x)) +c -(y_i - m(y)) )^2 ove c-a m(x) + m(y) =b
= somme_i ( a (x_i -m(x)) -(y_i -m(y))^2 + 2c somme ( a (x_i -m(x)) -(y_i -m(y)) + nc^2
poiche' il secondo addendo e' nullo essendo campioni centrati
= n Var (ax -y) +nc^2 = nVar (ax) + nVar (y) +2 n Cov(ax, -y) +n c^2=
= n( a^2 Var (x) - 2a Cov(x,y) + Var (y) +c
(quadratura) = n[ { a sigma(x) - Cov(x,y)/ sigma(x) }^2 + Var (y) - Cov(x,y)^2/Var(x) + c^2]
che e' minima quando a = Cov(x,y)/Var(x), c=0 cioe' b= m(y) - m(x) Cov(x,y)/Var(x)
Quindi, dati x =(x_1 ...x_n) ed y=(y_1 ..y_n), la retta ``migliore'' nel senso dei minimi quadrati e'
Y= Cov(x,y)/Var(x) X + m(y) - m(x) Cov(x,y)/Var(x)
mentre il valore mininimo dell'errore quadratico
min E(a,b) = Var (y) - Cov(x,y)^2/Var(x) = Var(y) [ 1 - Corr(x,y) ^2 ]
12-1-10 lezione 30 (ore 1 minuti 15) Riferimenti :[EB] cap 1.12-14 pagg. 22-35, [MA1] cap 1 pagg. 3-6, 10-13, 13-15, 19-22, [VV] cap. 1 pagg. 1-13.
La media pesata di media di sottocampioni (disgiunti) e' la media sul campione
Scale logaritmiche e correlazione
Volendo sondare altri tipi di dipendenza quando la correlazione e' piccola, per cui una dipendenza lineare non e' indicativa e la retta di regressione poco significativa,
per dipendenze del tipo
Y= a^X b si sonda la correlazione lineare tra x_1 ... x_n e log (y_1 +c) .... log (y_n +c)
scala logaritmica
Y= X^a b si sonda la correlazione lineare tra log (x_1 +d) .... e log (y_1 +c) ...
Errore assoluto e intervallo di incertezza
Dovendo fare dei calcoli o delle misure, necessariamente si useranno un numero finito di simboli e un tempo limitato e quindi, rispetto alla quantita' ideale da calcolare o misurare incognita per eccellenza, si introducono errori di approssimazione dovuti agli strumenti e alla necessita': capacita' di macchina, risoluzione dello strumento. Non solo: cause molteplici, singolarmente significative, nel complesso potrebbero introdurre altro tipo di errore. Una teoria completa e' ben fondata sul calcolo delle probabilita' e la statistica.
Un quadro semplificativo che da un'idea del tipo di problematica puo' essere il seguente:
x e' il numero che si vuole calcolare
v e' il risultato del computo o misura, o come si rappresenta con quanto si ha disposizione x
|v-x| si dira' errore assoluto
e >0 la stima nota dell'errore assoluto: |v-x| < e
[v-e , v+e] l'intervallo di incertezza di ampiezza 2e
la suggestiva scrittura con eguaglianza
x = v + o - e
e' in realta un'abbreviazione per le diseguaglianze
v-e < o = x < o = v+e
cioe' x in [v-e, v+e] ovvero v in [x-e, x+e]
In modo del tutto equivalente dal punto di vista matematico, pur riflettendo un diverso modo operativo, si puo' pensare piuttosto:
x e' il numero che si vuole calcolare
M una stima maggiore di x
m una stima minore di x
[M, m] intervallo di incertezza
nel caso si potra stimare x ponendo v = (m+M)/2 , e = (m-M)/2
e viceversa M= v + e , m = v-e
NOTA: \in certi casi (per esempio nelle approssimazioni per troncamento) si usano stime unilatere
v <o= x < o= v+e
ove la valutazione o la stima e' agli estermi dell'intervallo piuttostoi che nel mezzo.
Con questa notazione l'intervallo incertezza e' lungo e.
Nel seguito si assumeranno in genere le seguenti ipotesi
x > 0 , v > e >o= 0 , (v-e >e)
Errore realtivo
Fare un errore di 1 metro dovendo misurare la lunghezza totale delle coste italiane e' in molti casi del tutto irrilevante, ma lo stesso errore di 1 metro dovendo misurare l'altezza di un essere umano sembra gigantesco.
E' in effetti bene specificare il rapporto tra quanto si sbaglia e quanto deve essere misurato o si misura: tale quantitata' si chiama errore relativo:
e_r = |x-v|/ |x| < o = e /|x|
Questa nozione e' comodoa per motivi teorici specialmente dovendo trattare di calcolo numerico con macchine in ambito astratto.
Nella presente trattazione si preferisce definire con errore relativo la seconda:
e_r = |x-v|/ |v| < o = e /|v| = (M-m)/(M+m)
Approssimazione per troncamento e per arrotondamento
errore relativo nel troncamento
Svolgendo calcoli con metodo posizionale in base qualsiasi spesso e' necessario trascurare alcune delle cifre non intere (dopo la virgola). Si focalizza l'attenzione nel caso di metodo decimale.
Come introdotta nella lezione 25 del 3-12-09 si ricorda la notazione scientifica decimale:
ogni numero reale x non negativo puo' essere scritto in modo unico
x= a 10^k con a numero reale per cui 1/10 <o= a < 1, e k numero intero
il numero a si dice mantissa:
sara' del tipo 0, a_1 a_2 ..... con la prima cifra a_1 non 0 e non tutte le cifre eguali a 9.
si dice approssimazione per troncamento alla h-esima cifra della mantissa il numero
Tr_h(a) = 0 , a_1 ... a_h = a_1/10 + ... + a_h/10^h
si dice approssimazione per arrotondamento alla h-esima cifra della mantissa il numero
Ar_h(a) = 0 , a_1 ... a_h se a_{h+1} in {0, 1, 2, 3, 4}
Ar_h(a) = 0 , a_1 ... a_h + 1/10^h se a_{h+1} in {5, 6, 7, 8, 9}
(se a_h non e' 9 e' 0 , a_1 ... (a_h+1))
NOTA: non tutti gli autori dano questa definizione di approssimazione per arrotondamento.
Chiaramente Tr_h (a) < o= a <o= Tr_h(a) +1/10^h, l'errore di troncamento e 1/10^h, mentre
l'errore dell'arrotondamento e' la meta' di quello del troncamento.
Se x= a 10^k e lo si valuta con v = Tr_h(a) 10^k l'errore relativo e' controllato dal reciproco dell'intero che ha le cifre del troncato della mantissa
|x-v|/v = 0,0...0 a_{h+1} ... / Tr_h(a) <o= 1/10^h 1/0 , a_1 ... a_h = 1/a_1 ... a_h
Propagazione dell'errore nella somma, differenza e prodotto
Propagazione dell'errore assoluto in somma e differenza
se x = v +o- e, y =w +o- E cioe' v-e < o = x < o = v+e
w-E < o = y < o = w+E
sommando membro a membro v+w - e - E < o = x+y < o = v+w +e +E
cioe' x+y = (v+w) +o- (e+E)
Volendo fare lo stesso per la differenza
se x = v +o- e, y =w +o- E cioe' v-e < o = x < o = v+e
w-E < o = y < o = w+E
se a x si sottrae y si ottiene un numero
minore della differenza tra stima maggiore di x e stima minore di y
maggiore della differenza tra stima minore di x e stima maggiore di y
v-e -(w+E) <o= x-y <o= v+e - (w-E)
in altri termini
se x = v +o- e, y =w +o- E cioe' v-e < o = x < o = v+e
w-E < o = y < o = w+E
allora moltiplicando per -1 e invertendo le diseguaglianze relative ad y
x = v +o- e, -y =-w +o- E cioe' v-e < o = x < o = v+e
-w-E < o = - y < o = - w+E
ora sommando termine a termine si ottiene
x-y = (v-w) +o- (e+E)
con valutazione della diffrenza la differenza delle valutazioni
l'errore assoluto nella differenza si propaga come somma degli errori assoluti.
Propagazione dell'errore relativo nel prodotto
si supponga per semplicita' x, y, v, w, >0 e v> e, w> E:
se x = v +o- e, y =w +o- E cioe' 0< v-e < o = x < o = v+e
0< w-E < o = y < o = w+E
moltiplicando membro a membro si ottiene
prodotto dei minimi <o= xy <o= prodotto dei massimi
vw + eE - (ew+Ev) <o= xy <o= vw + eE + (ew+Ev)
cioe'
con valutazione del prodotto la somma del prodotto delle valutazioni e del prodotto degli errori
l'errore si propaga come somma dei prodotti tra un fattore e l'erroe dell'altro fattore.
Dividendo ew+Ev per vw +eE si ottiene una frazione minore di (ew+Ev)/vw = e/v +E/w = e_r +E_r
quindi
con valtazione la somma tra prodotto dlele valutazioni e prodotto degli errori
l'errore relativo del prodotto si propaga come la somma degli errori relativi.
La stima ottenuta puo' essere semplificata peggiorandola un po: infatti a mqaggior ragione si ha
vw - ( eE + ew +Ev) <o= xy <o= vw + (eE +ew+Ev)
qui la valutazione del prodotto e' semplicemente il prodotto delle valutazioni
con tale stima
l'errore relativo del prodotto si propaga come somma delgli errori relativi e del loro prodotto
(eE +ew+Ev)/vw = e/v E/w +e/v +E/w.
Quando si debba fare poche moltiplicazioni, e si abbiano errori relativi piccoli e_r < 1/10, E_r <1/10
conviene usare una regola non esatta:
xy circa vw +o- (ew+Ev)
Comunque nella pratica spesso conviene usare la notazione di valutazioni massime e minime, ootenendo la formulazione esatta e piu' precisa ancorche' implicitamente, e quindi
se 0< m < o = x <o= M
e 0< n <o = y <o= N
allora 0< mn < o= xy <o= MN
e quindi la valutazione e' (MN+mn)/2 , l'erroe (MN-mn)/2, quello relativo (MN-mn)/(MN+mn).
12-1-10 esercitazione 27 (minuti 45)
Esercizi su moda, mediana, media, retta di regressione.
Esercizio 2 parti a) e b) primo compitino 28 Novembre 2008 Matematica e Statistica C (Alberti):
40% dei clienti fa 1 solo ordine per importo medio di 40 eu
30% 2 30 eu per ordine
20% 3 30 eu per ordine
10% 4 40 eu per ordine
calcolare media e varianza di numero d'ordine per cliente
calcolare la spesa media per ordine
14-1-10 lezione 31 (minuti 45)
Propagazione dell'errore relativo nel quoziente
si supponga per semplicita' x, y, v, w, >0 e v> e, w> E:
se x = v +o- e, y =w +o- E cioe' 0< m(x)= v-e < o = x < o = v+e = M(x)
0< m(y) = w-E < o = y < o = w+E = M(y)
si ottiene
quoziente tra la valutazione minima di x e quella massima di y = m(x)/M(y)
<o=
x/y
<o=
quoziente tra la valutazione massima di x e quella minima di y = M(x)/m(y)
per cui
stimando il quoziente con la valutazione bilatera Q=1/2(M(x)/m(y) +m(x)/M(y)) si stima l'errore
con EQ= 1/2(M(x)/m(y) -m(x)/M(y)).
Volendo capire come si propaga l'errore conviene esplicitare il conto in termini di V M+o- e e di w +o- E, mettendo in riasalto il rapporto delle valutazioni:
Q= 1/2 ( (v+e)/(w-E) + (v-e)/(w+E)) = .... = (vw +eE)/ (w^2- E^2) = v/w ( 1 +e_rE_r)/ (1-E_r^2)=
= v/w + v/w E_r (e_r+E_r)/(1-E_r^2)
EQ= 1/2 ( (v+e)/(w-E) - (v-e)/(w+E)) = .... = (we +vE)/ (w^2- E^2) = v/w (e_r + E_r)/ (1-E_r^2)=
comunque si ha la semplice stima per la propagazione degli errori relativi
EQ_r =EQ/Q = (we +vE)/(vw +eE) = (e_r + E_r)/(1+e_r E_r) <o= e_r + E_r
cioe' l'errore relativo del quoziente si stima (come l'errore relativo del prodotto) con la somma degli errori relativi del dividendo e del divisore.
Quando si debba fare poche divisioni, e si abbiano errori relativi piccoli e_r < 1/10, E_r <1/10
conviene usare una regola non esatta:
x/y circa v/ w +o- v/w (e_r+E_r)
Comunque nella pratica spesso conviene usare la notazione di valutazioni massime e minime,
ottenendo la formulazione esatta anche se piu' implicitaimplicita data all'inizio.
Cifre significative in notazione decimale
Ci si limita ad esemplificare il concetto per numeri che siano mantisse.
L'idea intuitiva di numero di cifre significative, di una valutazione v per una grandezza x con stima dell'errore e: x =v +o- e, e' quella del numero di cifre consecutive subito dopo la virgola, a partire dalla prima non nulla, che non cambiano tra x e v.
Questa e' l'idea intuitiva. Conviene dare la seguente definizione:
Definizione: numero di cifre significative
dato v che sia una valutazione di un numero x con stima dell'errore e (v>e)
si dice numero delle cifre significative
N = parte intera (Log_{10} 1/ e_r ) +1
Da dove viene questa definizione: consideriamo x=a e v=b tra 1/10 ed 1 che abbiano le prime M cifre subito dopo la virgola eguali, rappresentandoli con allineamenti decimali non di periodo 9,
a=0, a_1 a_2 .... b=0,b_1b_2 ...
allora |a-b| e' minore stretto di 1/10^M (almeno una cifra dopo la M-esima nella rappresentazione decimale di a e' strettamente minore di 9 quindi a-b = (a_{M+1} -b_{M+1}) 1/10^{M+1} + ... <
9 /10^{M+1} +9 /10^{M+2} +... =1/10^M analogamente per b-a)
quindi e_r = |a-b| / b < 1/10^M x 10 passando ai logaritmi in base 10
Log_{10 } e_r < 1 - M cioe'
M < - Log_{10} e_r + 1 cioe'
M < Log_{10} 1/e_r + 1 cioe'
M - 1 < Log_{10} 1/e_r cioe'
M - 1 <o= parte intera di Log_{10} 1/e_r
14-1-10 esercitazione 28 (ore 1 minuti 15)
Esercizi sui limiti: rapporto di polinomi per la variabile che tende all'infinito, confronto con l'esponenziale ...
Esercizi su propagazione degli errori e cifre significative scelti tra i vecchi temi d'esame.
18-1-10 SECONDA PROVA IN ITINERE
I testi della seconda prova in itinere.
Le soluzioni della seconda prova in itinere.
12-2-10 RECUPERO DELLE PRIME DUE PROVE IN ITINERE
I testi della prova di recupero.
Le soluzioni della prova di recupero.
IL REGISTRO CONTINUA PER IL SECONDO SEMESTRE
CON QUESTO COLLEGAMENTO