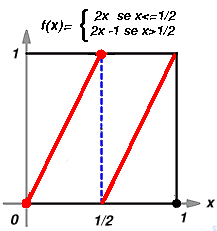
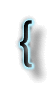Caos, Instabilita' e Impredicibilita'
Il concetto di caos e' usato sempre piu spesso nella letteratura divulgativa e
nel linguaggio comune.
Ad esso vengonoassociati altri concetti quali il concetto di disordine, di
comportamento apparentemente casuale, complesso, instabile.
Inmolti testi divulgativi si vede che spesso il caos viene associato alla
natura frattale di molti sistemi complessi.
In questo testo vogliamo precisare il significato di questi concetti, mostrando
anche come sia possibile definire loro stessi e le loro relazioni in modo
quantitativo e preciso. Vedremo come e' anche possibile mostrare queste
relazioni mediante figure (che fra l'altro risultano frattali)
che si ottengono visualizzando gli indicatori quantitativi di caos mediante
colori.
Veniamo quindi ad un primo approfondimento dei concetti di cui sopra.
Quando si pensa ad un sistema caotico ci sono due cose che vengono in mente:
![]() piccole variazioni della condizione iniziale portano a grandi
cambiamenti nell' evoluzione del sistema (sensibilita' al dato iniziale)
piccole variazioni della condizione iniziale portano a grandi
cambiamenti nell' evoluzione del sistema (sensibilita' al dato iniziale)
![]() il comportamento del sistema e' impredicibile e complesso
il comportamento del sistema e' impredicibile e complesso
Nel punto![]() la parola complesso puo significare che il
comportamento non ha descrizioni semplici, ci vuole molta informazione
per descivere il comportamento. In altre parole non bastano pochei nformazioni
iniziali per descrivere ilcomportamento del sistema pertempi lunghi. Ci vuole
molta informazione per descrivere il comportamento del sistema come ci vuole
molta informazione per descrivere una lunga serie di numeri estratti a caso,
mentre se inumeri sono determinati da una carta legge per descriverli basta
lalegge che li genera,non importa quanto sia lunga la sequenza. Cosiad esempio
per descrivere lasequenza
la parola complesso puo significare che il
comportamento non ha descrizioni semplici, ci vuole molta informazione
per descivere il comportamento. In altre parole non bastano pochei nformazioni
iniziali per descrivere ilcomportamento del sistema pertempi lunghi. Ci vuole
molta informazione per descrivere il comportamento del sistema come ci vuole
molta informazione per descrivere una lunga serie di numeri estratti a caso,
mentre se inumeri sono determinati da una carta legge per descriverli basta
lalegge che li genera,non importa quanto sia lunga la sequenza. Cosiad esempio
per descrivere lasequenza
101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010
sara necessaria meno informazione di quella che e' necessaria per descrivere
esattamente la sequenza
11100101010101010000101010100110101010111101010101010100111101101010`0110101010101010101101111101
infatti la prima e' generata da una semplice regola (e'periodica)
mentre per ricordare la seconda bisognera' ricordarsi tutte le cifre una per
una.
Il punto ![]() e' anche inteso nel seguente senso: piccole
perturbazioni inizialicambiano sensibilmente il comportamento a lungo
termine del sistema.
e' anche inteso nel seguente senso: piccole
perturbazioni inizialicambiano sensibilmente il comportamento a lungo
termine del sistema.
Si pensi al gioco del biliardo, se si vuole che una certa boccia vada in buca
dopo avere fatto diversi rimbalzi il tirova impostato con estrema precisione.
Piccoli errori iniziali si amplificheranno rimbalzo dopo rimbalzo e faranno in
modo che la posizione finale della boccia sara' imprevedibile nel casi in cui i
rimbalzi che ci proponiamo siano troppi rispetto alla nostra capacita' di fare
untiro preciso.
Questi due fenomeni appaiono ad esempio quando si pensa ai fenomeni metereologici. Si possono fare misure abbastanza precise sullo stato del tempo oggi (le condizioni iniziali del sistema), da queste si puo ricavare una previsione a breve termine, ma con il passare del tempo le previsioni diventano sempre meno affidabili. Analogamente prevedere dove si trovera' una certa boccia del biliardo dopo 1 rimbalzo e' relativamente semplice ma se ci proponiamo di prevedere dove si trovi dopo 20 rimbalzi sulle altre bocce la cosa e'praticamente impossibile. Una persona incaricata di descrivere ilcomportamento del tempo in una certa citta' per lunghi periodi, non potra' fare altro che fare una lista delle condizioni metereologicheche incontra ogni giorno, senza la possibilita'di trovare una regola semplice per spiegarle in blocco (tipo se oggi piove domani c'e' ilsole).
In matematica ci sono teoremi che assicurano che in molti casi ![]() e
e ![]() appaiono necessariamente insieme: l'uno implica l'altro.
appaiono necessariamente insieme: l'uno implica l'altro.
Laragione "pratica" di cio e' che a causa dell amplificarsidegli
errori iniziali conoscere il comportamento di un sistema perlungo tempo
"equivale" a conoscere la condizione iniziale con una grande
precisione, grande precisione significa conoscere idati con molte cifre
decimali e quindi molti bits di informazione sono necessari.
Inoltre piu aumenta il tempo per cui e' richiesta la conoscenzadel comportamento del sistema, piu la conoscenza della precisione iniziale deve essere accurata.
Ovviamente tradurre questo semplice ragionamento euristico equalitativo in
enunciati precisi e quantitativi e dimostrazioni matematiche non e' uncompito
facile e richiede l' uso di strumenti raffinati della matematica contemporanea
che noi in questa esposizione tratteremo in maniera informale ed in casi
particolari.
Nel seguito vedremo una verifica "sperimentale" diquesto principio in una famiglia di casi interessanti.
Le seguenti figure rappresentano la complessita' e la sensibilita'rispetto
al dato iniziale di una famiglia di sistemi. Nelle figure ogni puntorappresenta
un sistema, nella figura 2 il punto viene colorato aseconda che il sistema
corrispondente sia piu o meno sensibile aldato iniziale (gli errori si
amplificano velocemente), mentre nella figura 1 il punto viene colorato a
seconda che il comportamento delsistema sia piu o meno complesso.
|
|
|
|
Figura 1(Complessita) |
Figura 2 (Instabilita) |
Come si vede le due figure sono molto simili. Questa in un certo
senso e'una verifica sperimentale della stretta relazione che c'e'
fra ![]() e
e ![]() .
.
Ma cosa rappresentano esattamente le figure?
Per rispondere aquesto introdurremo un modo con cui si puo misurare quantitativamente
la complessita e l'instabilita, quindi abbiamo bisogno di precisare qualisono
gli oggetti con cui andremo a lavorare.
Cosa e' un sistema dinamico in matematica
Fino ad adesso abbiamo parlato di sistemi o di dinamica
senza specificare di preciso che cosa si intende.
In matematica, la prima cosa che si deve fare e' quella di dare definizioni
precise degli oggetti di cui si parla.
Se si costruiscono dei modelli allo scopo di studiare un certo fenomeno spesso
conviene considerare il modello piu semplice che presenta il detto fenomeno, in
modo da eliminare complicazioni inutili. Per studiare i misteri della dinamica
basta un modello semplicissimo che e' fatto di due oggetti:uno spazio e una
funzione.
Quando si parla di dinamica di un sistema (o di dinamica) si pensaal fatto
che il sistema parte son una condizione iniziale (in genere conosciuta in modo
piu o meno preciso) e poi si evolve nel tempo.
Il caso piu semplice di questo tipo di sistemi e' quello che in matematica si
chiama sistema dinamico a tempo discreto. E' una cosa semplice che da luogo a
comportamenti estremamente complicati e affascinanti.
La formalizzazione del concetto di sistema dinamico e' la seguente: unsistema dinamico e' una funzione che agisce su un certospazio, ovvero si ha uno spazio X e una funzione f da X in X. Ricordiamo che una funzione fè un modo di associare ad ogni punto x di Xun altropunto y=f(x) di X .
Data una condizione iniziale x la dinamica siottiene iterando
la funzione f. Cioe siparte da x , poi si va in
f(x) (che e' un altro punto del nostro spazio al quale si puo
applicare la f),quindi si va in f(f(x)) e
cosi via generando una traiettoria lunga quanto si vuole.
Ad esempio
Facciamo un esempio: consideriamo come spazio X l'insieme
dei numeri fra 0 e 1, estremi compresi (in notazione matematica siscrive
X=[0,1] ) quindi i punti x del nostro spazio saranno i
numeri compresi fra 0 e 1. Consideriamo la funzione fdefinita da f(x)=4x(1-x).
Questa funzione associa un numero in [0,1] ad un numero
in [0,1].
Ad esempio al numero![]() viene associato il
numero
viene associato il
numero ![]() . Nella seguente figura e' illustrato il
grafico di f.
. Nella seguente figura e' illustrato il
grafico di f.
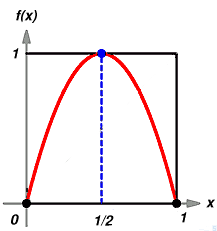
La dinamica del sistema si ottiene iterando la f ,cioe
se la condizione iniziale (al tempo 0) e' un certo![]() ,allora al
tempo 1 avremo
,allora al
tempo 1 avremo![]() , e poi
, e poi![]() ,e cosi via
,e cosi via![]() perogni n. Equivalentemente si avra'
perogni n. Equivalentemente si avra'![]() ,
,![]() .
.
Ad esempio la traiettoria che parte dal punto![]() sara' la
seguente:
sara' la
seguente:![]()
e cosi via ottenendo sempre 0 (cioe![]() per tutti gli
per tutti gli![]() ) perche si continuera' ad avere
) perche si continuera' ad avere![]() .In
generale si dicono punti fissi i punti
.In
generale si dicono punti fissi i punti ![]() per cui
per cui![]() . Quando la dinamica arriva in uno di questi vi si
ferma per sempre.
. Quando la dinamica arriva in uno di questi vi si
ferma per sempre.
Se facciamo partire la dinamica da altri punti, diversi da ½ in
generale potranno accadere cose diverse, per esempio la traiettoria potrebbe
convergere verso un orbita periodica, cioe gli![]() ripeteranno periodicamente gli stessi valori (ad es ...
ripeteranno periodicamente gli stessi valori (ad es ...![]() ).
).
In altri casi si potra avere una successione di valori che
sembrano uscire a ``casaccio'' come ad esempio se ![]() siavra'
siavra' ![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() .
.
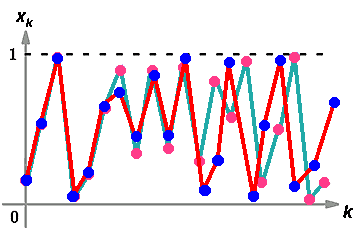
Se disegnamo un grafico di questa traiettoria otterremo una figura simile alla
seguente. Anche se l'apparenza e' quella di una successione di punti a caso
quella che e' disegnata qui sotto e'un'orbita deterministica: ogni punto e'
determinato dal precedente(mediante l'applicazione della funzione f ).
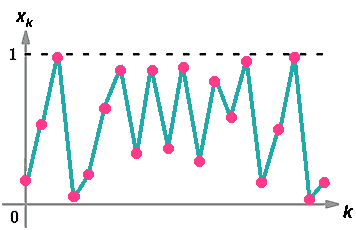
L'errore iniziale
Vediamo piu approfonditamente il punto ![]() nel nostro esempio.
nel nostro esempio.
Vediamo ad esempio come un piccolo errore iniziale viene amplificato nei
passi successivi delladinamica.
Nella figura sotto e' riportata anche la dinamica (indicata con ![]() ) di un punto che parte con una condizione iniziale
) di un punto che parte con una condizione iniziale ![]() leggermente maggiore di
leggermente maggiore di![]() .Come si vede la distanza
fra i passi successivi
.Come si vede la distanza
fra i passi successivi ![]() della dinamica aumenta fino
ad essere confrontabile con la dimensione dello spazio stesso, per poi
fluttuare casualmente (e' ovvio che i due punti non possono allontanarsi
indefinitamente, visto che l'intero spazio che consideriamo ha diametro 1).
della dinamica aumenta fino
ad essere confrontabile con la dimensione dello spazio stesso, per poi
fluttuare casualmente (e' ovvio che i due punti non possono allontanarsi
indefinitamente, visto che l'intero spazio che consideriamo ha diametro 1).
Vediamo piu in dettaglio come si genera questo allontanarsi di orbite che partono inizialmente vicine.
Nella figura si vede che due condizioni iniziali che partono vicine, con un
errore E(0) vengono mandate dalla f
in condizioni finali che distano E(1). Dalla figura si vede
che ![]() ,ovvero l'errore finale e' dato dall errore iniziale
moltiplicato peril coefficente angolare della secante al grafico passante per
,ovvero l'errore finale e' dato dall errore iniziale
moltiplicato peril coefficente angolare della secante al grafico passante per ![]() e
e ![]() .
.
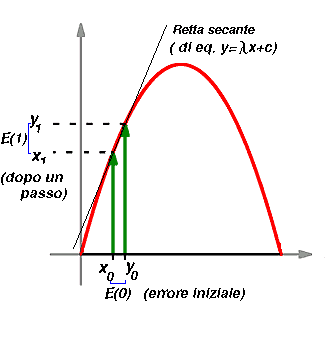
Nella figura il coefficente angolare e' piu o meno 2, dunque in questo caso
dopo unpasso l'errore si raddoppia.
Chi dei lettori ha seguito un corsodi analisi matematica ricordera' che il
coefficente angolare della retta secante di due punti molto vicini ha a che
fare con un concettomolto famoso: la derivata
.
Per la precisione esiste un
teorema che ci assicura che ![]() dove
dove![]() e' un punto compreso fra
e' un punto compreso fra ![]() e
e![]() .Se
.Se ![]() e
e ![]() sono molto vicini anche
sono molto vicini anche ![]() e' molto vicino a
e' molto vicino a ![]() e siccome la
derivata e` una funzione continua si ha che ilsuo valore in
e siccome la
derivata e` una funzione continua si ha che ilsuo valore in ![]() e` molto vicino al valore calcolato in
e` molto vicino al valore calcolato in ![]() e
quindi possiamo dire che approssimativamente si ha che l'errore iniziale
viene moltiplicato per (il valore assoluto della) derivata della funzione
in
e
quindi possiamo dire che approssimativamente si ha che l'errore iniziale
viene moltiplicato per (il valore assoluto della) derivata della funzione
in ![]() cioe
cioe![]() .
.
|
|
|
Ad esempio Il lettore potra' facilmente intuire che se consideriamo un sistema con f'(x)>a>1per
ogni x in [0,1] allora punti che partono
inizialmente molto vicini si allontanano avelocita' esponenziale perche ogni
volta l'errore sara' moltiplicato perun mumero maggiore dia, dunque Questo succede ad esempio nel sistema rappresentato nella seguente
figura
Qui infatti f'(x)=2 per "quasi" ogni x. Quindi piccoli errori iniziali vengono raddoppiati ad ogni passo. |
Il coefficente di Lyapunov: una misura quantitativa della velocita di amplificazione dell errore iniziale.
In generale siavra' che se ![]() e'la
traiettoria che parte da
e'la
traiettoria che parte da![]() l'errore al passo n
sara' approssimativamente
l'errore al passo n
sara' approssimativamente![]() moltiplicando l'errore
iniziale per i valori assoluti delle derivate nei punti incontrati durante la
dinamica. Siccome gli
moltiplicando l'errore
iniziale per i valori assoluti delle derivate nei punti incontrati durante la
dinamica. Siccome gli![]() potranno essere tutti
diversi (anche minori di 1) l'errore iniziale viene moltiplicato per una
successione di numeri diversi.
potranno essere tutti
diversi (anche minori di 1) l'errore iniziale viene moltiplicato per una
successione di numeri diversi.
Comestimare allora la velocita' di allontanamento di traiettorie chepartono vicine?
Cipossiamo chiedere "in media" per quanto e' moltiplicatol'errore ad ogni passo.
Per rispondere a questa domanda immaginiamo che esista un tale coefficente
di dilatazione medio.
Allora si potra'scrivere ![]() da cui
da cui
![]() e
e
![]() ,
,
![]()
e se la quantita![]() (la media aritmetica dei
logaritmi delle derivate che si incontrano lungola traiettoria) converge ,
quando n diventa molto grande verso un numero
(la media aritmetica dei
logaritmi delle derivate che si incontrano lungola traiettoria) converge ,
quando n diventa molto grande verso un numero ![]() allora
allora ![]() equindi
equindi
![]()
il numero che contaallora e' la media dei logaritmi delle derivate lungo la traiettoria.
Questo numero ![]() viene chiamato Coefficente
di Lyapunov della funzione f nelpunto
viene chiamato Coefficente
di Lyapunov della funzione f nelpunto![]() .
.
Piu grande e'![]() epiu grande e' la velocita' (media) di allontanamento di traiettorie che
partono vicine.
epiu grande e' la velocita' (media) di allontanamento di traiettorie che
partono vicine. ![]() puoanche essere negativo,
in quel caso l'errore iniziale invece di aumentare diminuira' e in questo caso
traiettorie che partono inizialmente vicine a
puoanche essere negativo,
in quel caso l'errore iniziale invece di aumentare diminuira' e in questo caso
traiettorie che partono inizialmente vicine a![]() si
avvicineranno sempre piu alla traiettoria di
si
avvicineranno sempre piu alla traiettoria di ![]() .
.
|
|
|
Per esempio il sistema dato da f(x)=(1\2)*x ha |
Ricapitolando
Dato un sistema dinamico ed una condizione iniziale esisteun modo di
ottenere un numero che viene chiamato coefficente diLyapunov ... e ...
|
|
|
|
|
*Orbite che partono vicine si allontanano |
|
|
|
|
|
*Traiettorie che partono vicine restano vicine |
|
|
|
E per |
L'informazione
Abbiamo detto che per noi un comportamento complesso e' un comportamento la cui
evoluzione richiede (al passare del tempo) molta informazione per essere
descritta.
In questo paragrafo si chiarisce cosa si intende per quantita di informazione e
come la misuriamo.
Ci sono molti approcci
possibili alla definizione del concetto di informazione e quantita di
informazionecontenuta in una sequenza di caratteri (che in linguaggio
informatico si chiama anche stringa). Noi vorremmo avere una nozione che ci permetta,
data una singola stringa S, di ottenere un numero I(S) che considereremo come
'la quantita di informazione contenuta in S.
La misura della quantita di informazione contenuta in S quindi dipendera solo
da S e non da altre informazioni sul contesto in cui appare la stringa.
Come molti sanno, in ogni computer esistono dei programmi che comprimono
i files. Questi programmi sono chiamati in gergo'zippatori'
(Winzip,gzip, Bzip2 e molti altri).
![]() Cosafa di preciso uno zippatore?
Lo zippatore prende un file grosso e spesso lo codifica in un file piu
piccolo, che puo essere archiviato risparmiando spazio sul disco del computer.
Il file compresso poi all occorrenza puo essere decodificato per riottenereil
file originale, cosi come era. Senza perdere informazioni.
Cosafa di preciso uno zippatore?
Lo zippatore prende un file grosso e spesso lo codifica in un file piu
piccolo, che puo essere archiviato risparmiando spazio sul disco del computer.
Il file compresso poi all occorrenza puo essere decodificato per riottenereil
file originale, cosi come era. Senza perdere informazioni.
La maggior parte dei documenti di testo (scritti in italiano adesempio) puo essere compressa ad un terzo della dimensione iniziale,ad esempio unfile lungo 30K viene archiviato in un file compresso di10K.
![]() Comefanno?
Comefanno?
Gli zippatori sfruttano le ridondanze statistiche della stringa inconsiderazione per codificarla in modo piu coinciso.
Facciamo un primo esempio stupido, che e' ancora molto lontano da quello che viene fatto in pratica da questi programmi:
Se io voglio ricordarmi il numero33333333333333355555555555555511111111111 bastera' che ricordi "15 volte 3,11 volte 5,11 volte 1", in questo modo sfrutto le ripetizioni per comprimere la stringa.
Un'altra idea piu furba, che puo essere usata per comprimere stringhe di testo, per esempio e' quella di codificare una lettera alla volta, usando codici piu corti per le lettere piu frequenti, e lasciare i codici piu lunghi per le lettere che appaiono piu raramente. Questo approccio e' usato ad esempio nell antichissimo codice Morse, dove infatti la lettera E che e' molto frequente viene codificata con "." mentre la Q che appare piu raramennteviene codificata con "--.-"
Questa idea pero, per essere
messa inpratica richiede un conoscenza preventiva della lingua alla quale
appartiene il testo che deve essere codificato. Un lingua dove la Qe' piu
frequente della E viene codificata in modo inefficiente dal codice Morse.
Bisogna dire inoltre che i caratteri non appaiono indipendentemente , ad
esempio in italiano una Q molto probabilmente dopo e' seguita da una U.
Quindi, come il letteresi puo immaginare anche queste relazioni possono essere
struttate per ottenere codici piu efficienti. Questo tipo di regole richiedono
perola conoscenza del contesto in cui appare la stringa da codificare.
Gli zippatori invece codificano una stringa senza sapere da dove proviene, in un certo senso durante la codifica questi zippatori costruiscono un dizionario (di parole che appaiono nella stringa) cheli aiuta a sfruttare le regolarita della stringa.
Come funzionano precisamente? Clicca qui per altre informazioni sulla compressione dati
![]() Come possiamo applicare queste cose
per misurare l'informazione?
Come possiamo applicare queste cose
per misurare l'informazione?
L'idea e' molto semplice: siccome nel file compresso e' contenuta tutta l'informazione necessaria per ricostruire il file originale possiamo pensare che la lunghezza del file compresso sia una misura(approssimata per eccesso) della quantita di informazione contenuta nel file originale.
Quindi se si vuole misurare l'informazione contenuta in S, lo si comprime e si considera la lunghezza del file compresso.
Ovviamente questa misura approssimata sara' accurata se lo zippatore e' efficiente e comprime la stringa in maniera ottimale.
Lo zippatore perfetto non esiste, ma quelli che sono comunemente usati sono abbastanza buoni per i nostri scopi.
![]() Un altro approccio piu teorico:
Un altro approccio piu teorico:
Bisogna dire che se lo zippatore perfetto non esiste, esiste una teoria perfetta della quantita di informazione che in un certo sensosi riferisce ad uno zippatore perfetto: la complessita di Kolmogorov. Molto velocemente accenneremo a cosa si tratta senza entrare nei dettagli.
La complessita di Kolmogorov di una stringa e' la lunghezza del minimo
programma (che eseguito da un certo computer) restituisce come output la
stringa. In un certo senso l'associazione stringa ![]() minimo programma
puo essere pensata come una compressione ottimaledella stringa. Purtroppo
questa associazione non puo essere fatta da nessun algoritmo (da nessuna
procedura effettiva finita).
minimo programma
puo essere pensata come una compressione ottimaledella stringa. Purtroppo
questa associazione non puo essere fatta da nessun algoritmo (da nessuna
procedura effettiva finita).
Piu precisamente si puo dimostrare che non puo esistere nessun programma (scritto in un qualsiasi linguaggio di programmazione) che calcoli la complessita di Kolmogorov delle stringhe.
Quindi la complessita di Kolmogorov e'uno strumento teorico moltopotente (che fra l'altro consente di dimostrare in modo sempliceteoremi come il famoso teorema di incompletezza di Goedel) ma non e'utilizzabile in pratica.
Per una esposizione divulgativa molto divertente di questa teoria clicca
qui Chiacchierata sulla teoria algoritmica
dell informazione (V.Benci)
![]() Complessitae rapporto di compressione
Complessitae rapporto di compressione
Adesso vediamo come di applica la quantita' di informazione per misurare il
grado di caoticita-complessita di un sistema.
Abbiamo un sistema dinamico che genera una traiettoria ![]() chee' una succesione di punti dello spazio.
chee' una succesione di punti dello spazio.
Adesso dividiamo lo spazio in 2 regioni: A e B (attenzione,
per i sempici sistemi che considereremo bastano due regioni, ma in generale
bisogna considerare anche piu di due regioni), e associamo alla
traiettoria ![]() la stringa ottenuta sostituendo ad
ogni punto della traiettoria l'insieme( A o B) che lo contiene,
in questo modo siottiene da una traiettoria di n punti una stringa binaria di n caratteri.
la stringa ottenuta sostituendo ad
ogni punto della traiettoria l'insieme( A o B) che lo contiene,
in questo modo siottiene da una traiettoria di n punti una stringa binaria di n caratteri.
Ad esempio se si considera la mappa
logistica come sistema dinamico, lospazio e' [0,1], una buona scelta dei due insiemi e' data daA=[0,1/2),
B=[1/2,1]la successione ottenuta prima ![]()
![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() si trasforma nella seguente
successione AABBAB...
si trasforma nella seguente
successione AABBAB...
Quindi ad una traiettoria di lunghezza n
e'associata una stringa binaria s(n).
Adesso, come discusso prima misuriamo l'informazione contenuta in s(n) utilizzando il nostro algoritmo di compressione Z, comprimiamo s(n), ottenendo una stringa Z(s(n))di cui misuriamo la lunghezza e questa sara'la quantita di informazione contenuta in s(n).
Riassumendo Indichiamo con I la funzione che misura laquantita di informazione contenuta nelle stringhe e quindi definiamo
I(s(n))=lunghezza( Z(s(n))).
Come abbiamo visto, da un sistema dinamico
si possono ottenere traiettorie lunghe quanto si vuole e quindi stringhe
associate lunghe quanto sivuole.
Se il sistema e' caotico la stringa non sara' descritta da regolesemplici e quindi conterra' molta informazione (rispetto alla sualunghezza), mentre la stringa associata ad un sistema prevedibile (ades un sistema periodico)conterr a' poca informazione.
Quello chevogliamo fare adesso e' definire un criterio che individui lestringhe piu caotiche, siccome abbiamo a chefare con stringhe di v aria lunghezza consideriamo la quantita' media di informazione contenuta in un carattere della stringa.
Quindi considereremo la seguente quantita' K(s(n))=I(s(n))/n (con nmolto grande) .
K(s(n)) sara' anche chiamato rapporto
di compressione della stringa s(n)
(infatti e' il rapporto fra la lunghezza della stringa originale e quello della
stringa compressa).
Questo rapporto sara' un numero alto se la stringa contiene molta informazione
e viceversa sara' un numero basso se la stringa contiene poca informazione e
quindi si comprime molto rispetto alla sua lunghezza, questo indica chelo
zippatore ha trovato delle forti regolarita' nella stringa ed usa queste
regolarita' per comprimerla al meglio.
Come abbiamo fatto le figure

Vediamo come si
ottengono le figure: abbiamo detto che un sistema dinamico e'una coppia
(spazio,funzione) la quale agisce sullo spazio e genera una dinamica.
Supponiamo che da ora in poi lo spazio che ciinteressa sia l'intervallo [0,1]
e consideriamo diverse funzioni, che daranno luogo a diversi tipi
di dinamica.
Prima ad esempio era stata considerata la funzione f(x)=4x(1-x)
sostituendo un altro numero al posto del 4 sipossono avere
tipi di dinamica completamente diversi.
Cioe, se siconsidera la famiglia di funzioni f(x, p)=4 p x(1-x) al
variare di p fra 0 e 1 sipossono
avere diversi tipi di dinamica, da una dinamica periodica (quando p
e' piccolo) che hacoefficente di Lyapunov negativo in tutti i punti ad
una dinamicacaotica (quando pe' grande) con coefficiente
positivo.
Questa famiglia ad un parametro di sistemi dinamici e' moltofamosa e
studiata(mappe logistiche). Per qualche ulteriore spiegazione rimandiamo
al seguente link sulla Mappa
logistica .
Nel nostro caso si considera
una famiglia a due parametri di funzioni dall intervallo in se stesso f
(x,p,q) date dalla formula
f(x,p,q)=P(p,Q(q,x))
dove
P(x)=4p(x(1-x))
e
Q(x)=4q(x(1-x))
Come si vede quindi ogni funzione f (x,p,q) e'data dalla composizione di due funzioni logistiche con parametri anche diversi. I parametri possono ambedue variare fra fra 0 e 1 . Ogni possibile coppia di parametri (p,q) (chevariano fra 0 e 1) puo essere considerata come un punto di un quadrato. Ogni punto del quadrato che contiene la figura quindi corrisponde ad una funzione. Si calcola il coefficente di Lyapunov di questa funzione (rispetto a qualche punto iniziale x scelto a caso, grosso modo in questi casi il coefficente non dipende dal punto) e si colora il punto del quadrato in base al numero che si ottiene.
Il risultato sono quegli strani frattali pieni di tentacoli che sivedono nelle figure. Il primo a disegnare questo tipo di figure e'stato Markus (Scientific American, sept 1991) per questomotivo in genere questo tipo di frattali vengono chiamati frattalidi Markus-Lyapunov.
Per disegnare le figure che rappresentano la complessita' si ripete la stessa costruzione considerando le stesse funzioni di prima si calcola il rapporto di compressione invece del coefficente di Lyapunov.
Quindi ricapitolando per disegnare le figure:
Frattali di Markus-Lyapunov
consideriamo un punto (p,q) del quadrato, a questo punto corrispondera' una funzione f (x,p,q).
Si considera f (x,p,q) ,si sceglie un punto x a caso nel nostro spazio [0,1] e si calcola il coefficente di Lyapunov della funzione f (x,p,q) nel punto x.
In base al valore che si ottiene si colora il punto del quadrato.

I punti con coefficente di Lyapunov basso saranno colorati con colori scuri,
mentre i punti che corrispondono a sistemi dinamici aventi coefficente di
Lyapunov piu alto saranno colorati cono colori piu chiari.
Frattali della complessita'
Per disegnare la figura:
consideriamo un punto (p,q) del quadrato, a questo punto corrispondera' una funzione f (x,p,q).
Si considera f (x,p,q) ,si sceglie un punto x a caso nel nostro spazio [0,1] si sceglie una partizione che genera una stringa simbolica e si calcola il rapporto di compressione della mappa f (x,p,q) nel punto x.
In base al valore che si ottiene
si colora il punto del quadrato.

Figura qui sopra
I punti con complessita' (rapporto di compressione) alta saranno
colorati con colori chiari mentre quelli cono complessita bassa saranno
colorati con colori piu scuri.
Ad esempio nella figura qui sopra i punti con rapporto di compressione molto
vicino a 0 sono neri.